Beyond Data Scarcity: A Frequency-Driven Framework for Zero-Shot Forecasting

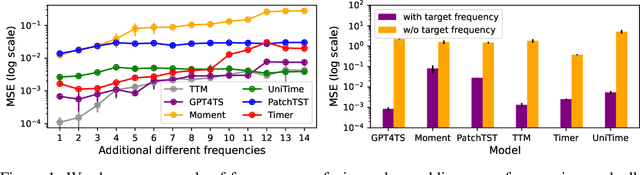
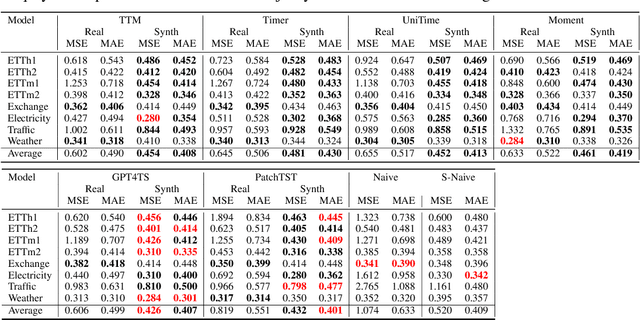
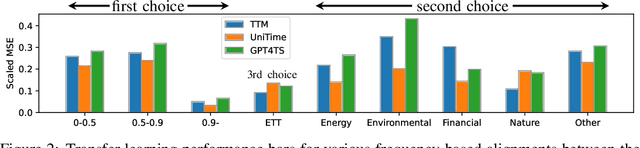
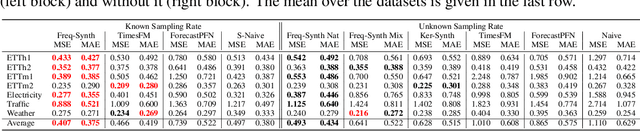
Time series forecasting is critical in numerous real-world applications, requiring accurate predictions of future values based on observed patterns. While traditional forecasting techniques work well in in-domain scenarios with ample data, they struggle when data is scarce or not available at all, motivating the emergence of zero-shot and few-shot learning settings. Recent advancements often leverage large-scale foundation models for such tasks, but these methods require extensive data and compute resources, and their performance may be hindered by ineffective learning from the available training set. This raises a fundamental question: What factors influence effective learning from data in time series forecasting? Toward addressing this, we propose using Fourier analysis to investigate how models learn from synthetic and real-world time series data. Our findings reveal that forecasters commonly suffer from poor learning from data with multiple frequencies and poor generalization to unseen frequencies, which impedes their predictive performance. To alleviate these issues, we present a novel synthetic data generation framework, designed to enhance real data or replace it completely by creating task-specific frequency information, requiring only the sampling rate of the target data. Our approach, Freq-Synth, improves the robustness of both foundation as well as nonfoundation forecast models in zero-shot and few-shot settings, facilitating more reliable time series forecasting under limited data scenarios.

SQT -- std $Q$-target

Std $Q$-target is a conservative, actor-critic, ensemble, $Q$-learning-based algorithm, which is based on a single key $Q$-formula: $Q$-networks standard deviation, which is an "uncertainty penalty", and, serves as a minimalistic solution to the problem of overestimation bias. We implement SQT on top of TD3/TD7 code and test it against the state-of-the-art (SOTA) actor-critic algorithms, DDPG, TD3 and TD7 on seven popular MuJoCo and Bullet tasks. Our results demonstrate SQT's $Q$-target formula superiority over TD3's $Q$-target formula as a conservative solution to overestimation bias in RL, while SQT shows a clear performance advantage on a wide margin over DDPG, TD3, and TD7 on all tasks.

PDExplain: Contextual Modeling of PDEs in the Wild

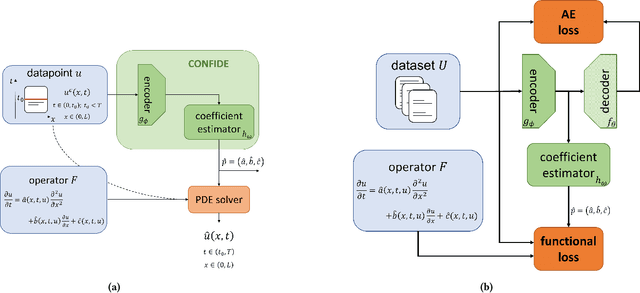
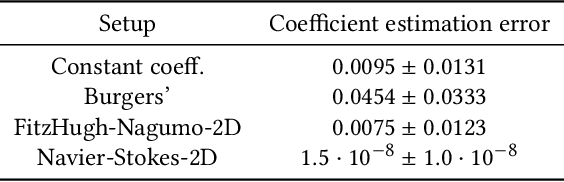
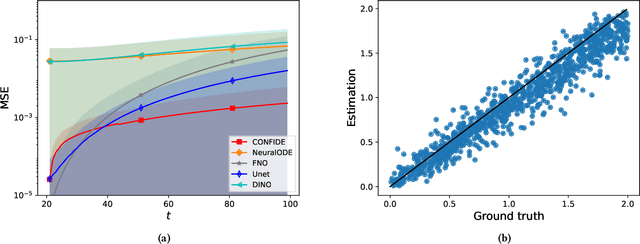
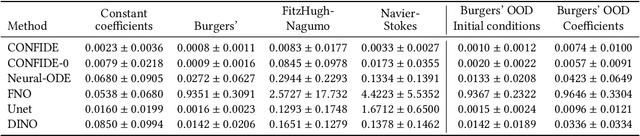
We propose an explainable method for solving Partial Differential Equations by using a contextual scheme called PDExplain. During the training phase, our method is fed with data collected from an operator-defined family of PDEs accompanied by the general form of this family. In the inference phase, a minimal sample collected from a phenomenon is provided, where the sample is related to the PDE family but not necessarily to the set of specific PDEs seen in the training phase. We show how our algorithm can predict the PDE solution for future timesteps. Moreover, our method provides an explainable form of the PDE, a trait that can assist in modelling phenomena based on data in physical sciences. To verify our method, we conduct extensive experimentation, examining its quality both in terms of prediction error and explainability.

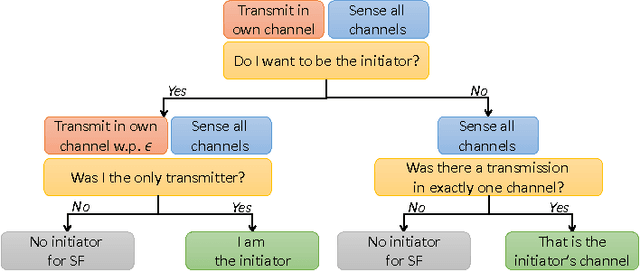
Multi-user Communication Networks: A Coordinated Multi-armed Bandit Approach

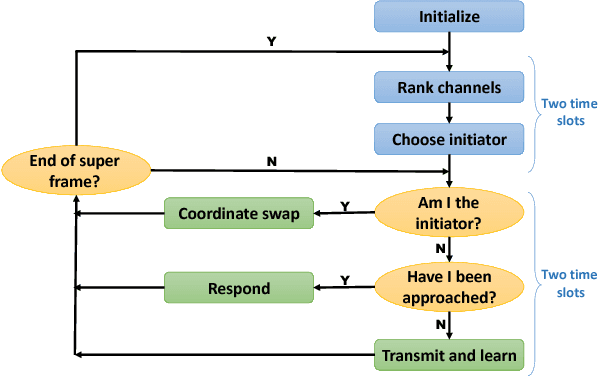
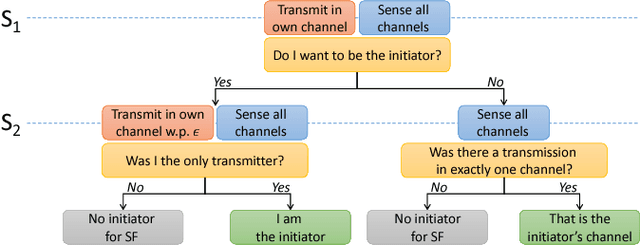
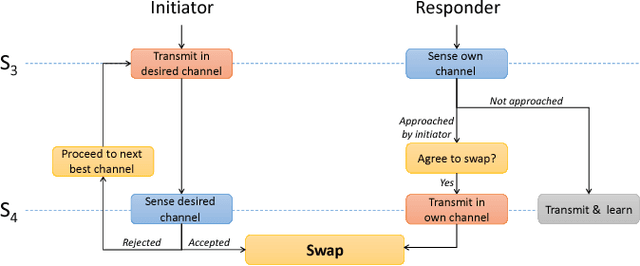
Communication networks shared by many users are a widespread challenge nowadays. In this paper we address several aspects of this challenge simultaneously: learning unknown stochastic network characteristics, sharing resources with other users while keeping coordination overhead to a minimum. The proposed solution combines Multi-Armed Bandit learning with a lightweight signalling-based coordination scheme, and ensures convergence to a stable allocation of resources. Our work considers single-user level algorithms for two scenarios: an unknown fixed number of users, and a dynamic number of users. Analytic performance guarantees, proving convergence to stable marriage configurations, are presented for both setups. The algorithms are designed based on a system-wide perspective, rather than focusing on single user welfare. Thus, maximal resource utilization is ensured. An extensive experimental analysis covers convergence to a stable configuration as well as reward maximization. Experiments are carried out over a wide range of setups, demonstrating the advantages of our approach over existing state-of-the-art methods.

Multi-user lax communications: a multi-armed bandit approach

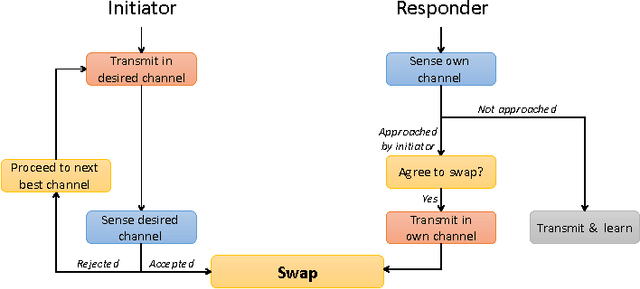
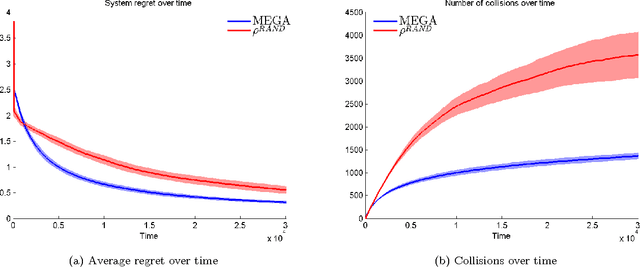
Inspired by cognitive radio networks, we consider a setting where multiple users share several channels modeled as a multi-user multi-armed bandit (MAB) problem. The characteristics of each channel are unknown and are different for each user. Each user can choose between the channels, but her success depends on the particular channel chosen as well as on the selections of other users: if two users select the same channel their messages collide and none of them manages to send any data. Our setting is fully distributed, so there is no central control. As in many communication systems, the users cannot set up a direct communication protocol, so information exchange must be limited to a minimum. We develop an algorithm for learning a stable configuration for the multi-user MAB problem. We further offer both convergence guarantees and experiments inspired by real communication networks, including comparison to state-of-the-art algorithms.

Concurrent bandits and cognitive radio networks

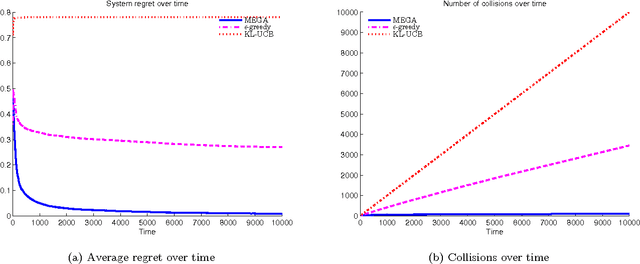
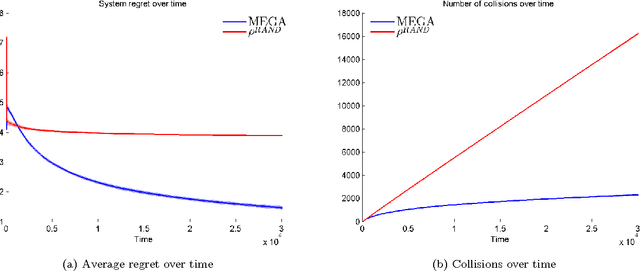
We consider the problem of multiple users targeting the arms of a single multi-armed stochastic bandit. The motivation for this problem comes from cognitive radio networks, where selfish users need to coexist without any side communication between them, implicit cooperation or common control. Even the number of users may be unknown and can vary as users join or leave the network. We propose an algorithm that combines an $\epsilon$-greedy learning rule with a collision avoidance mechanism. We analyze its regret with respect to the system-wide optimum and show that sub-linear regret can be obtained in this setting. Experiments show dramatic improvement compared to other algorithms for this setting.

Decoupling Exploration and Exploitation in Multi-Armed Bandits

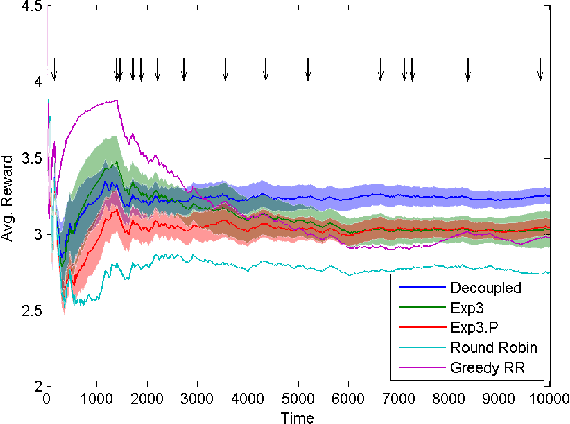
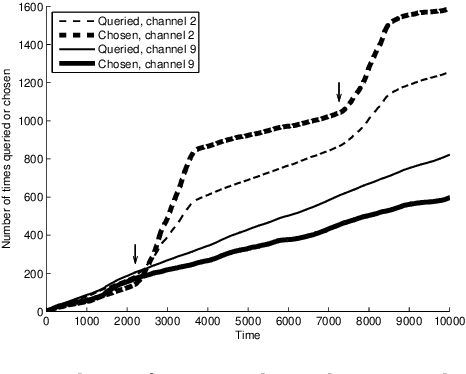
We consider a multi-armed bandit problem where the decision maker can explore and exploit different arms at every round. The exploited arm adds to the decision maker's cumulative reward (without necessarily observing the reward) while the explored arm reveals its value. We devise algorithms for this setup and show that the dependence on the number of arms, k, can be much better than the standard square root of k dependence, depending on the behavior of the arms' reward sequences. For the important case of piecewise stationary stochastic bandits, we show a significant improvement over existing algorithms. Our algorithms are based on a non-uniform sampling policy, which we show is essential to the success of any algorithm in the adversarial setup. Finally, we show some simulation results on an ultra-wide band channel selection inspired setting indicating the applicability of our algorithms.