Beyond Data Scarcity: A Frequency-Driven Framework for Zero-Shot Forecasting

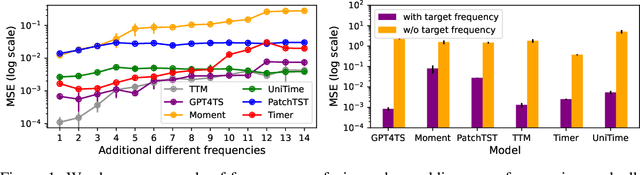
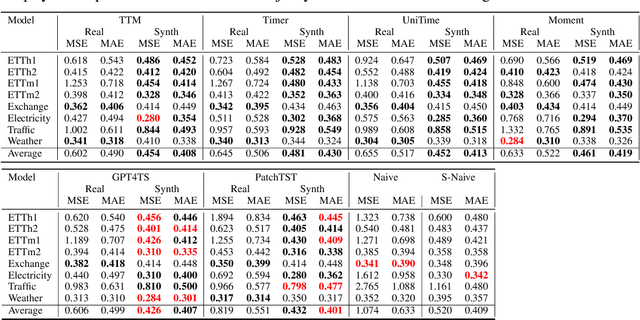
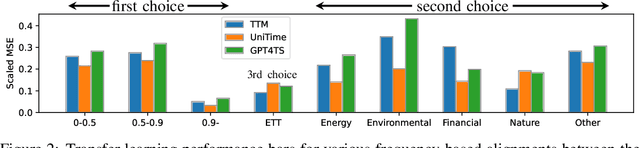
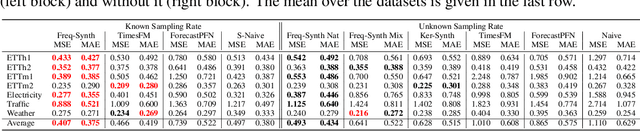
Time series forecasting is critical in numerous real-world applications, requiring accurate predictions of future values based on observed patterns. While traditional forecasting techniques work well in in-domain scenarios with ample data, they struggle when data is scarce or not available at all, motivating the emergence of zero-shot and few-shot learning settings. Recent advancements often leverage large-scale foundation models for such tasks, but these methods require extensive data and compute resources, and their performance may be hindered by ineffective learning from the available training set. This raises a fundamental question: What factors influence effective learning from data in time series forecasting? Toward addressing this, we propose using Fourier analysis to investigate how models learn from synthetic and real-world time series data. Our findings reveal that forecasters commonly suffer from poor learning from data with multiple frequencies and poor generalization to unseen frequencies, which impedes their predictive performance. To alleviate these issues, we present a novel synthetic data generation framework, designed to enhance real data or replace it completely by creating task-specific frequency information, requiring only the sampling rate of the target data. Our approach, Freq-Synth, improves the robustness of both foundation as well as nonfoundation forecast models in zero-shot and few-shot settings, facilitating more reliable time series forecasting under limited data scenarios.

Data Augmentation Policy Search for Long-Term Forecasting

Data augmentation serves as a popular regularization technique to combat overfitting challenges in neural networks. While automatic augmentation has demonstrated success in image classification tasks, its application to time-series problems, particularly in long-term forecasting, has received comparatively less attention. To address this gap, we introduce a time-series automatic augmentation approach named TSAA, which is both efficient and easy to implement. The solution involves tackling the associated bilevel optimization problem through a two-step process: initially training a non-augmented model for a limited number of epochs, followed by an iterative split procedure. During this iterative process, we alternate between identifying a robust augmentation policy through Bayesian optimization and refining the model while discarding suboptimal runs. Extensive evaluations on challenging univariate and multivariate forecasting benchmark problems demonstrate that TSAA consistently outperforms several robust baselines, suggesting its potential integration into prediction pipelines.