Benchmarks for Reinforcement Learning with Biased Offline Data and Imperfect Simulators

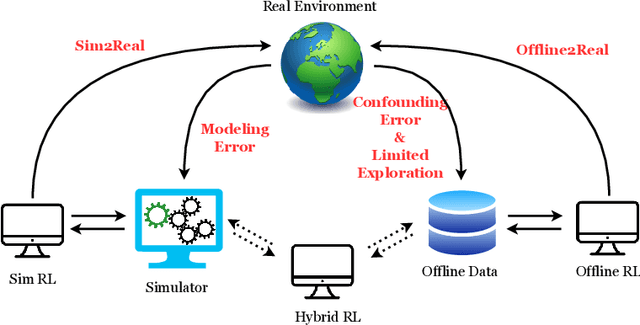
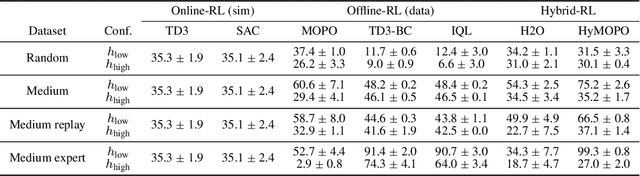
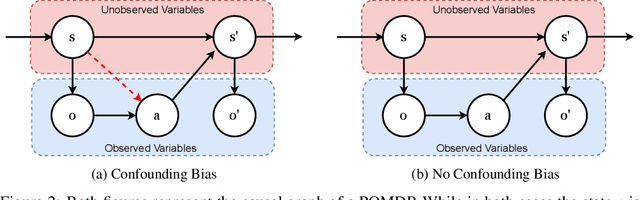
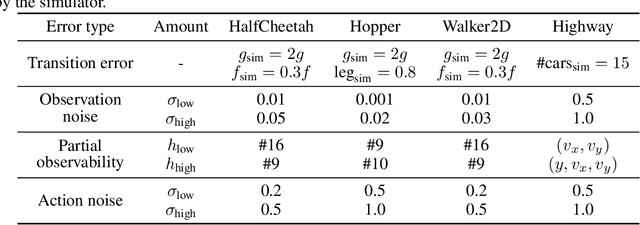
In many reinforcement learning (RL) applications one cannot easily let the agent act in the world; this is true for autonomous vehicles, healthcare applications, and even some recommender systems, to name a few examples. Offline RL provides a way to train agents without real-world exploration, but is often faced with biases due to data distribution shifts, limited coverage, and incomplete representation of the environment. To address these issues, practical applications have tried to combine simulators with grounded offline data, using so-called hybrid methods. However, constructing a reliable simulator is in itself often challenging due to intricate system complexities as well as missing or incomplete information. In this work, we outline four principal challenges for combining offline data with imperfect simulators in RL: simulator modeling error, partial observability, state and action discrepancies, and hidden confounding. To help drive the RL community to pursue these problems, we construct ``Benchmarks for Mechanistic Offline Reinforcement Learning'' (B4MRL), which provide dataset-simulator benchmarks for the aforementioned challenges. Our results suggest the key necessity of such benchmarks for future research.

Asymmetric Face Recognition with Cross Model Compatible Ensembles

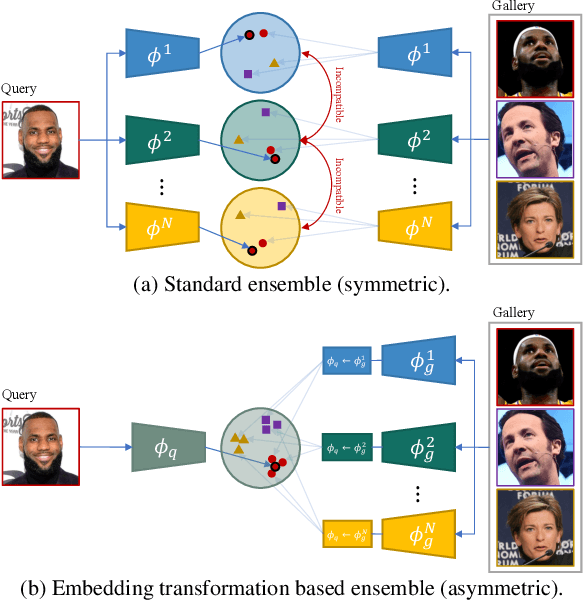
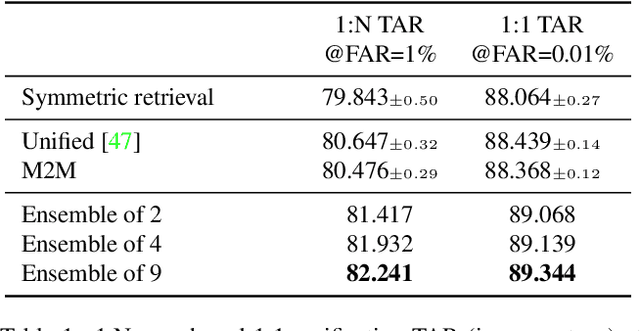
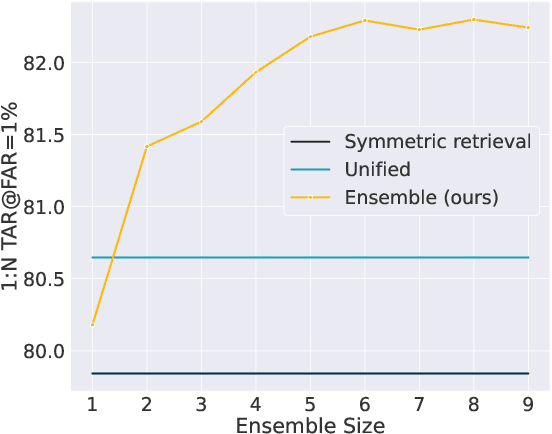
The asymmetrical retrieval setting is a well suited solution for resource constrained face recognition. In this setting a large model is used for indexing the gallery while a lightweight model is used for querying. The key principle in such systems is ensuring that both models share the same embedding space. Most methods in this domain are based on knowledge distillation. While useful, they suffer from several drawbacks: they are upper-bounded by the performance of the single best model found and cannot be extended to use an ensemble of models in a straightforward manner. In this paper we present an approach that does not rely on knowledge distillation, rather it utilizes embedding transformation models. This allows the use of N independently trained and diverse gallery models (e.g., trained on different datasets or having a different architecture) and a single query model. As a result, we improve the overall accuracy beyond that of any single model while maintaining a low computational budget for querying. Additionally, we propose a gallery image rejection method that utilizes the diversity between multiple transformed embeddings to estimate the uncertainty of gallery images.

PDExplain: Contextual Modeling of PDEs in the Wild

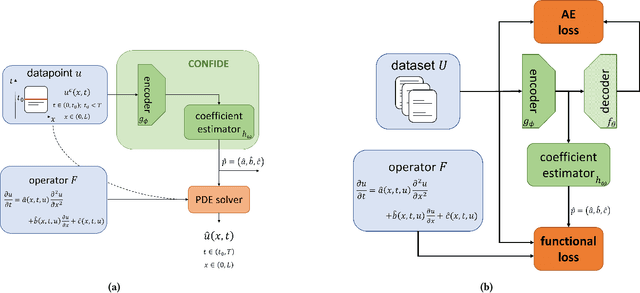
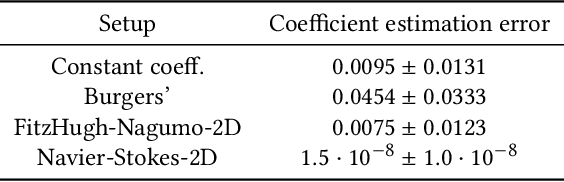
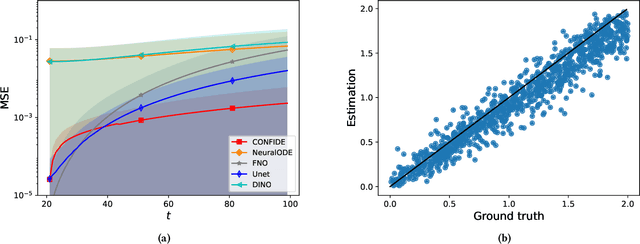
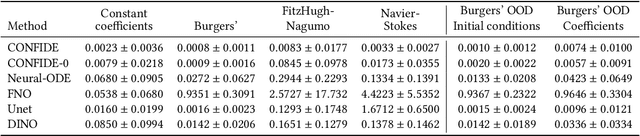
We propose an explainable method for solving Partial Differential Equations by using a contextual scheme called PDExplain. During the training phase, our method is fed with data collected from an operator-defined family of PDEs accompanied by the general form of this family. In the inference phase, a minimal sample collected from a phenomenon is provided, where the sample is related to the PDE family but not necessarily to the set of specific PDEs seen in the training phase. We show how our algorithm can predict the PDE solution for future timesteps. Moreover, our method provides an explainable form of the PDE, a trait that can assist in modelling phenomena based on data in physical sciences. To verify our method, we conduct extensive experimentation, examining its quality both in terms of prediction error and explainability.

Generative ODE Modeling with Known Unknowns

In several crucial applications, domain knowledge is encoded by a system of ordinary differential equations (ODE). A motivating example is intensive care unit patients: The dynamics of some vital physiological variables such as heart rate, blood pressure and arterial compliance can be approximately described by a known system of ODEs. Typically, some of the ODE variables are directly observed while some are unobserved, and in addition many other variables are observed but not modeled by the ODE, for example body temperature. Importantly, the unobserved ODE variables are ``known-unknowns'': We know they exist and their functional dynamics, but cannot measure them directly, nor do we know the function tying them to all observed measurements. Estimating these known-unknowns is often highly valuable to physicians. Under this scenario we wish to: (i) learn the static parameters of the ODE generating each observed time-series (ii) infer the dynamic sequence of all ODE variables including the known-unknowns, and (iii) extrapolate the future of the ODE variables and the observations of the time-series. We address this task with a variational autoencoder incorporating the known ODE function, called GOKU-net for Generative ODE modeling with Known Unknowns. We test our method on videos of pendulums with unknown length, and a model of the cardiovascular system.