PDExplain: Contextual Modeling of PDEs in the Wild
Paper and Code
Mar 28, 2023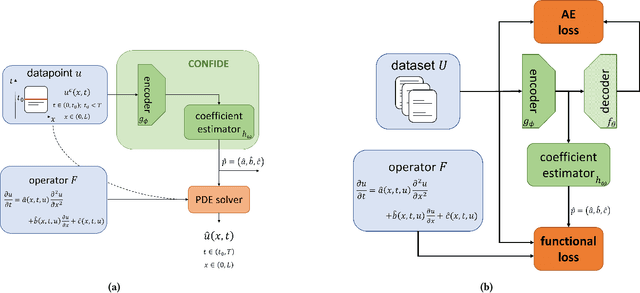
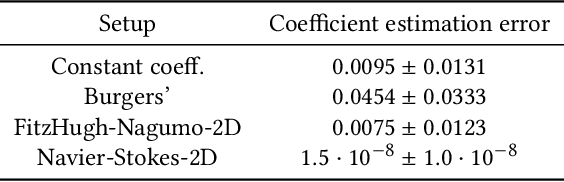
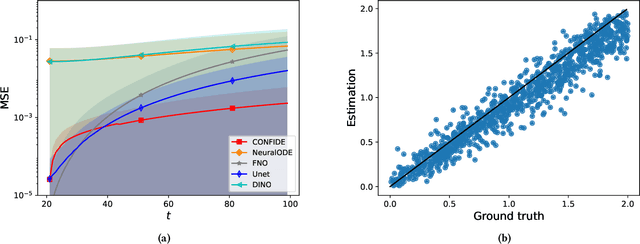
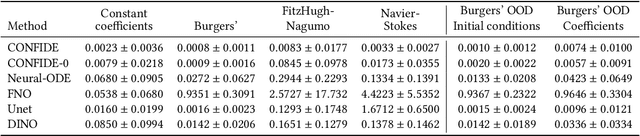
We propose an explainable method for solving Partial Differential Equations by using a contextual scheme called PDExplain. During the training phase, our method is fed with data collected from an operator-defined family of PDEs accompanied by the general form of this family. In the inference phase, a minimal sample collected from a phenomenon is provided, where the sample is related to the PDE family but not necessarily to the set of specific PDEs seen in the training phase. We show how our algorithm can predict the PDE solution for future timesteps. Moreover, our method provides an explainable form of the PDE, a trait that can assist in modelling phenomena based on data in physical sciences. To verify our method, we conduct extensive experimentation, examining its quality both in terms of prediction error and explainability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge