Decoupling Exploration and Exploitation in Multi-Armed Bandits
Paper and Code
Jun 30, 2012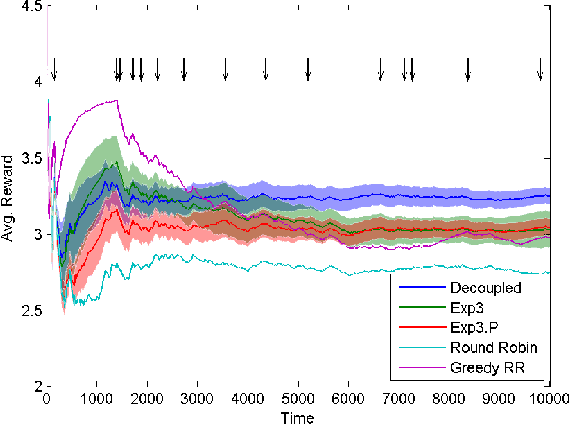
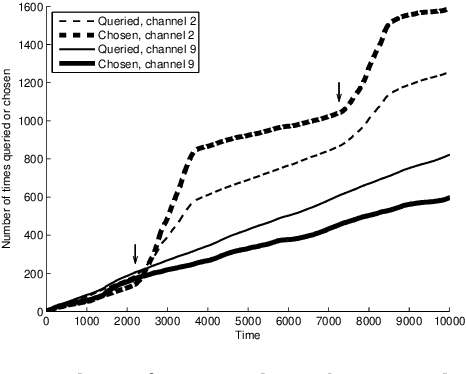
We consider a multi-armed bandit problem where the decision maker can explore and exploit different arms at every round. The exploited arm adds to the decision maker's cumulative reward (without necessarily observing the reward) while the explored arm reveals its value. We devise algorithms for this setup and show that the dependence on the number of arms, k, can be much better than the standard square root of k dependence, depending on the behavior of the arms' reward sequences. For the important case of piecewise stationary stochastic bandits, we show a significant improvement over existing algorithms. Our algorithms are based on a non-uniform sampling policy, which we show is essential to the success of any algorithm in the adversarial setup. Finally, we show some simulation results on an ultra-wide band channel selection inspired setting indicating the applicability of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge