Concurrent bandits and cognitive radio networks
Paper and Code
Apr 22, 2014
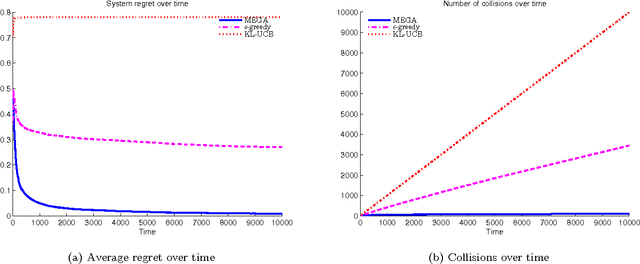
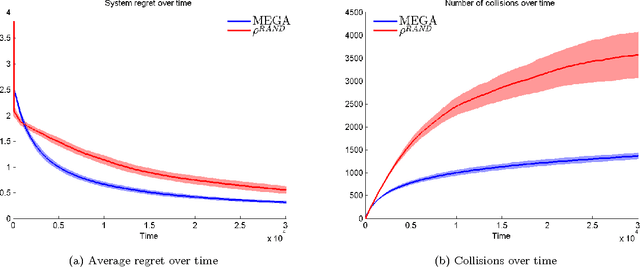
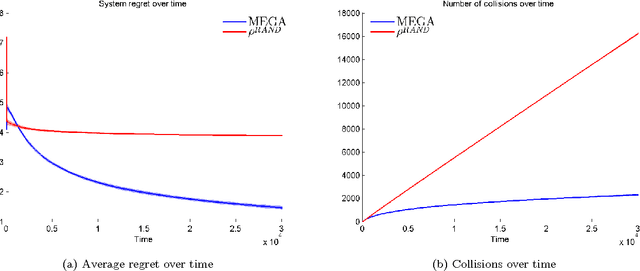
We consider the problem of multiple users targeting the arms of a single multi-armed stochastic bandit. The motivation for this problem comes from cognitive radio networks, where selfish users need to coexist without any side communication between them, implicit cooperation or common control. Even the number of users may be unknown and can vary as users join or leave the network. We propose an algorithm that combines an $\epsilon$-greedy learning rule with a collision avoidance mechanism. We analyze its regret with respect to the system-wide optimum and show that sub-linear regret can be obtained in this setting. Experiments show dramatic improvement compared to other algorithms for this setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge