Elucidating the Design Choice of Probability Paths in Flow Matching for Forecasting

Flow matching has recently emerged as a powerful paradigm for generative modeling and has been extended to probabilistic time series forecasting in latent spaces. However, the impact of the specific choice of probability path model on forecasting performance remains under-explored. In this work, we demonstrate that forecasting spatio-temporal data with flow matching is highly sensitive to the selection of the probability path model. Motivated by this insight, we propose a novel probability path model designed to improve forecasting performance. Our empirical results across various dynamical system benchmarks show that our model achieves faster convergence during training and improved predictive performance compared to existing probability path models. Importantly, our approach is efficient during inference, requiring only a few sampling steps. This makes our proposed model practical for real-world applications and opens new avenues for probabilistic forecasting.

Tuning Frequency Bias of State Space Models

State space models (SSMs) leverage linear, time-invariant (LTI) systems to effectively learn sequences with long-range dependencies. By analyzing the transfer functions of LTI systems, we find that SSMs exhibit an implicit bias toward capturing low-frequency components more effectively than high-frequency ones. This behavior aligns with the broader notion of frequency bias in deep learning model training. We show that the initialization of an SSM assigns it an innate frequency bias and that training the model in a conventional way does not alter this bias. Based on our theory, we propose two mechanisms to tune frequency bias: either by scaling the initialization to tune the inborn frequency bias; or by applying a Sobolev-norm-based filter to adjust the sensitivity of the gradients to high-frequency inputs, which allows us to change the frequency bias via training. Using an image-denoising task, we empirically show that we can strengthen, weaken, or even reverse the frequency bias using both mechanisms. By tuning the frequency bias, we can also improve SSMs' performance on learning long-range sequences, averaging an 88.26% accuracy on the Long-Range Arena (LRA) benchmark tasks.

Gated Recurrent Neural Networks with Weighted Time-Delay Feedback

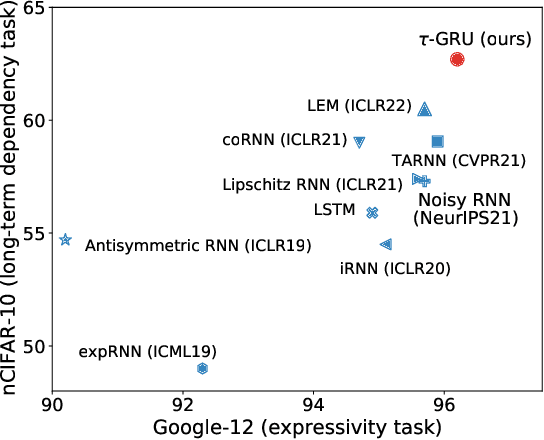
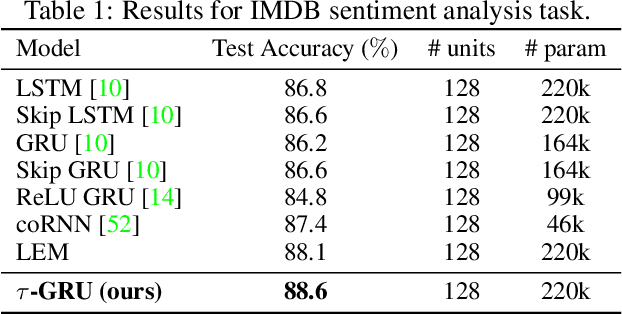
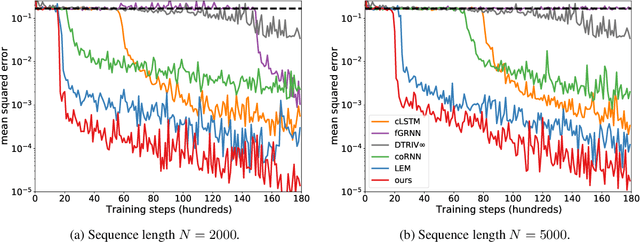
We introduce a novel gated recurrent unit (GRU) with a weighted time-delay feedback mechanism in order to improve the modeling of long-term dependencies in sequential data. This model is a discretized version of a continuous-time formulation of a recurrent unit, where the dynamics are governed by delay differential equations (DDEs). By considering a suitable time-discretization scheme, we propose $\tau$-GRU, a discrete-time gated recurrent unit with delay. We prove the existence and uniqueness of solutions for the continuous-time model, and we demonstrate that the proposed feedback mechanism can help improve the modeling of long-term dependencies. Our empirical results show that $\tau$-GRU can converge faster and generalize better than state-of-the-art recurrent units and gated recurrent architectures on a range of tasks, including time-series classification, human activity recognition, and speech recognition.

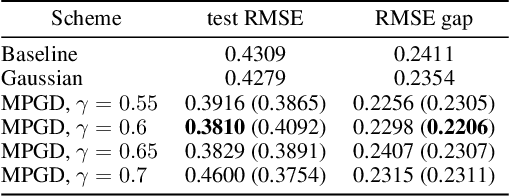
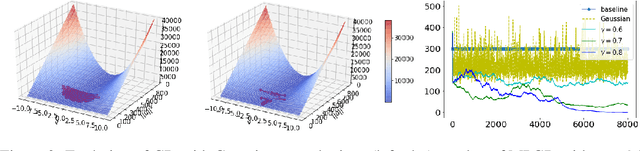
Chaotic Regularization and Heavy-Tailed Limits for Deterministic Gradient Descent

Recent studies have shown that gradient descent (GD) can achieve improved generalization when its dynamics exhibits a chaotic behavior. However, to obtain the desired effect, the step-size should be chosen sufficiently large, a task which is problem dependent and can be difficult in practice. In this study, we incorporate a chaotic component to GD in a controlled manner, and introduce multiscale perturbed GD (MPGD), a novel optimization framework where the GD recursion is augmented with chaotic perturbations that evolve via an independent dynamical system. We analyze MPGD from three different angles: (i) By building up on recent advances in rough paths theory, we show that, under appropriate assumptions, as the step-size decreases, the MPGD recursion converges weakly to a stochastic differential equation (SDE) driven by a heavy-tailed L\'evy-stable process. (ii) By making connections to recently developed generalization bounds for heavy-tailed processes, we derive a generalization bound for the limiting SDE and relate the worst-case generalization error over the trajectories of the process to the parameters of MPGD. (iii) We analyze the implicit regularization effect brought by the dynamical regularization and show that, in the weak perturbation regime, MPGD introduces terms that penalize the Hessian of the loss function. Empirical results are provided to demonstrate the advantages of MPGD.

NoisyMix: Boosting Robustness by Combining Data Augmentations, Stability Training, and Noise Injections

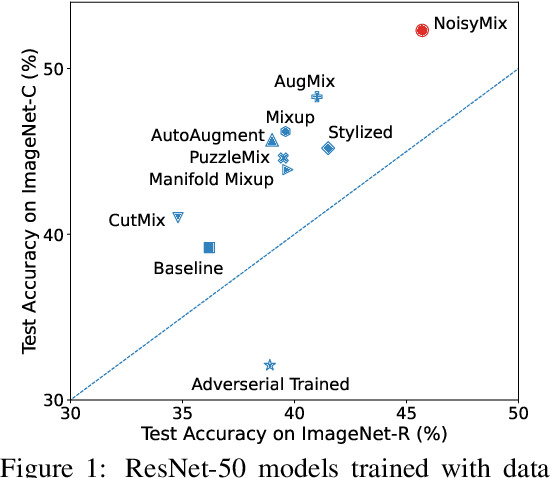
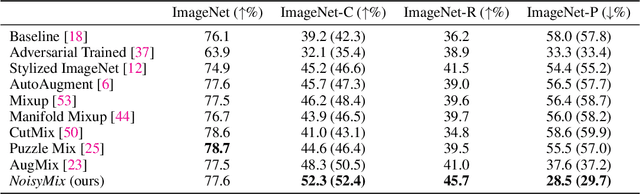
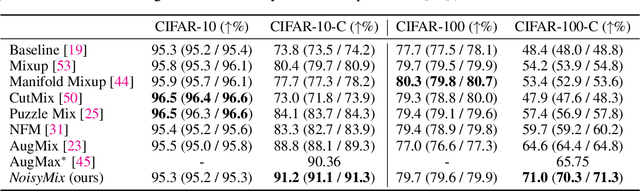
For many real-world applications, obtaining stable and robust statistical performance is more important than simply achieving state-of-the-art predictive test accuracy, and thus robustness of neural networks is an increasingly important topic. Relatedly, data augmentation schemes have been shown to improve robustness with respect to input perturbations and domain shifts. Motivated by this, we introduce NoisyMix, a training scheme that combines data augmentations with stability training and noise injections to improve both model robustness and in-domain accuracy. This combination promotes models that are consistently more robust and that provide well-calibrated estimates of class membership probabilities. We demonstrate the benefits of NoisyMix on a range of benchmark datasets, including ImageNet-C, ImageNet-R, and ImageNet-P. Moreover, we provide theory to understand implicit regularization and robustness of NoisyMix.

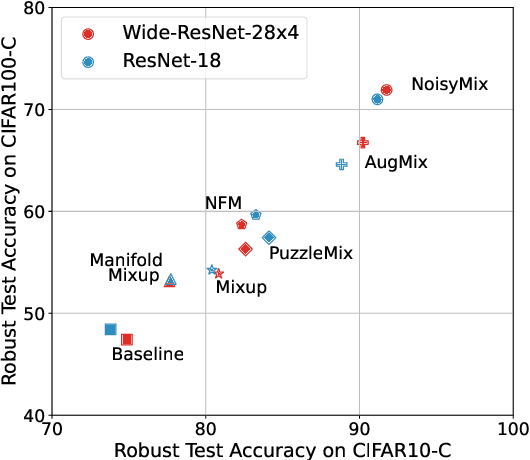
Noisy Feature Mixup

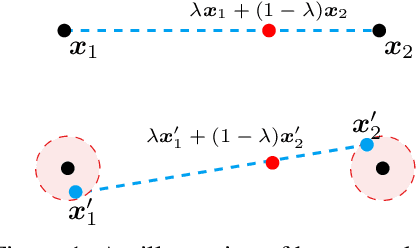
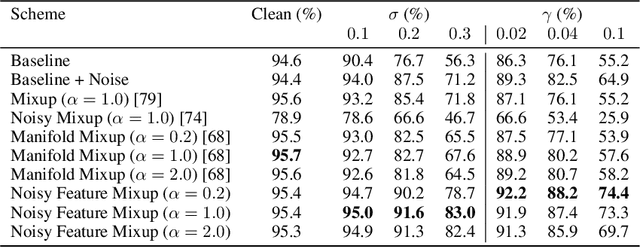
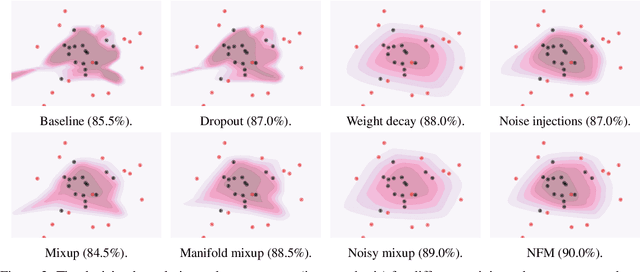
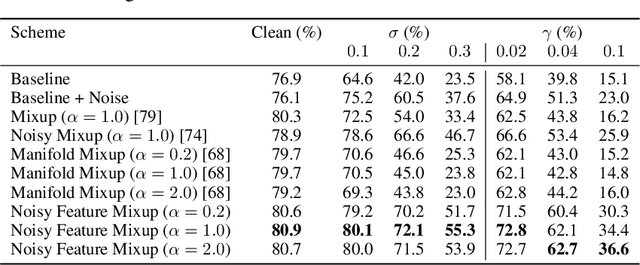
We introduce Noisy Feature Mixup (NFM), an inexpensive yet effective method for data augmentation that combines the best of interpolation based training and noise injection schemes. Rather than training with convex combinations of pairs of examples and their labels, we use noise-perturbed convex combinations of pairs of data points in both input and feature space. This method includes mixup and manifold mixup as special cases, but it has additional advantages, including better smoothing of decision boundaries and enabling improved model robustness. We provide theory to understand this as well as the implicit regularization effects of NFM. Our theory is supported by empirical results, demonstrating the advantage of NFM, as compared to mixup and manifold mixup. We show that residual networks and vision transformers trained with NFM have favorable trade-offs between predictive accuracy on clean data and robustness with respect to various types of data perturbation across a range of computer vision benchmark datasets.

Noisy Recurrent Neural Networks

We provide a general framework for studying recurrent neural networks (RNNs) trained by injecting noise into hidden states. Specifically, we consider RNNs that can be viewed as discretizations of stochastic differential equations driven by input data. This framework allows us to study the implicit regularization effect of general noise injection schemes by deriving an approximate explicit regularizer in the small noise regime. We find that, under reasonable assumptions, this implicit regularization promotes flatter minima; it biases towards models with more stable dynamics; and, in classification tasks, it favors models with larger classification margin. Sufficient conditions for global stability are obtained, highlighting the phenomenon of stochastic stabilization, where noise injection can improve stability during training. Our theory is supported by empirical results which demonstrate improved robustness with respect to various input perturbations, while maintaining state-of-the-art performance.

Understanding Recurrent Neural Networks Using Nonequilibrium Response Theory

Recurrent neural networks (RNNs) are brain-inspired models widely used in machine learning for analyzing sequential data. The present work is a contribution towards a deeper understanding of how RNNs process input signals using the response theory from nonequilibrium statistical mechanics. For a class of continuous-time stochastic RNNs (SRNNs) driven by an input signal, we derive a Volterra type series representation for their output. This representation is interpretable and disentangles the input signal from the SRNN architecture. The kernels of the series are certain recursively defined correlation functions with respect to the unperturbed dynamics that completely determine the output. Exploiting connections of this representation and its implications to rough paths theory, we identify a universal feature -- the response feature, which turns out to be the signature of tensor product of the input signal and a natural support basis. In particular, we show that the SRNNs can be viewed as kernel machines operating on a reproducing kernel Hilbert space associated with the response feature.

Predicting Rare Events in Multiscale Dynamical Systems using Machine Learning

We study the problem of rare event prediction for a class of slow-fast nonlinear dynamical systems. The state of the system of interest is described by a slow process, whereas a faster process drives its evolution. By taking advantage of recent advances in machine learning, we present a data-driven method to predict the future evolution of the state. We show that our method is capable of predicting a rare event at least several time steps in advance. We demonstrate our method using numerical experiments on two examples and discuss the mathematical and broader implications of our results.