Elucidating the Design Choice of Probability Paths in Flow Matching for Forecasting

Flow matching has recently emerged as a powerful paradigm for generative modeling and has been extended to probabilistic time series forecasting in latent spaces. However, the impact of the specific choice of probability path model on forecasting performance remains under-explored. In this work, we demonstrate that forecasting spatio-temporal data with flow matching is highly sensitive to the selection of the probability path model. Motivated by this insight, we propose a novel probability path model designed to improve forecasting performance. Our empirical results across various dynamical system benchmarks show that our model achieves faster convergence during training and improved predictive performance compared to existing probability path models. Importantly, our approach is efficient during inference, requiring only a few sampling steps. This makes our proposed model practical for real-world applications and opens new avenues for probabilistic forecasting.

Hybrid Models for Mixed Variables in Bayesian Optimization

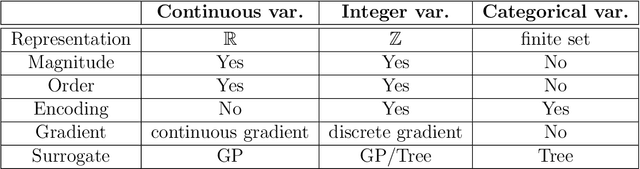
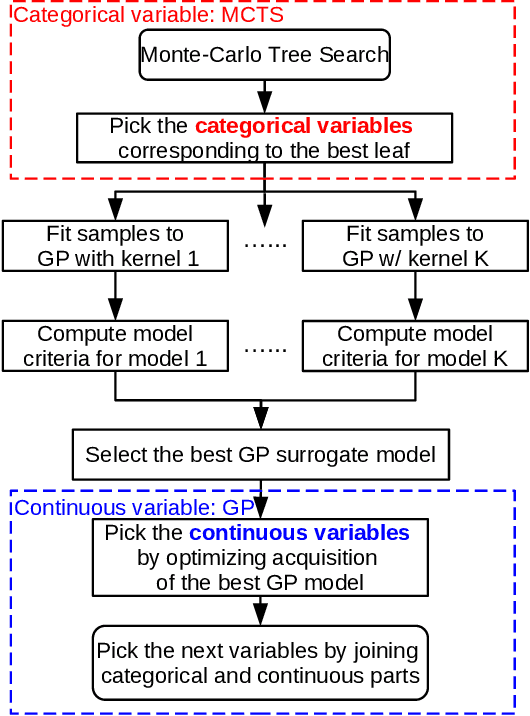
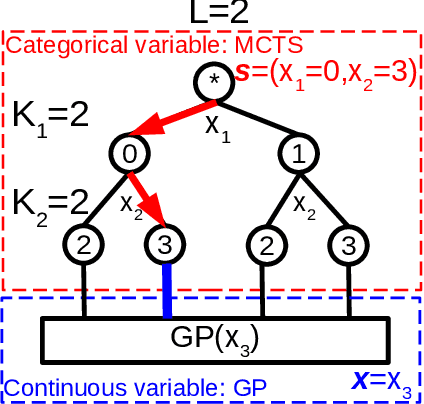
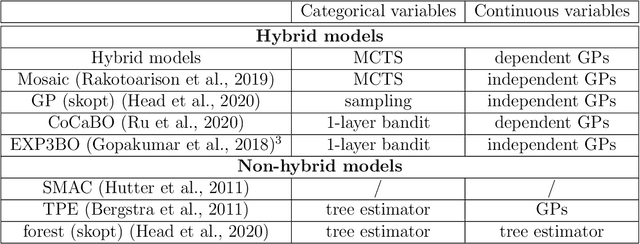
We systematically describe the problem of simultaneous surrogate modeling of mixed variables (i.e., continuous, integer and categorical variables) in the Bayesian optimization (BO) context. We provide a unified hybrid model using both Monte-Carlo tree search (MCTS) and Gaussian processes (GP) that encompasses and generalizes multiple state-of-the-art mixed BO surrogates. Based on the architecture, we propose applying a new dynamic model selection criterion among novel candidate families of covariance kernels, including non-stationary kernels and associated families. Different benchmark problems are studied and presented to support the superiority of our model, along with results highlighting the effectiveness of our method compared to most state-of-the-art mixed-variable methods in BO.

Non-smooth Bayesian Optimization in Tuning Problems

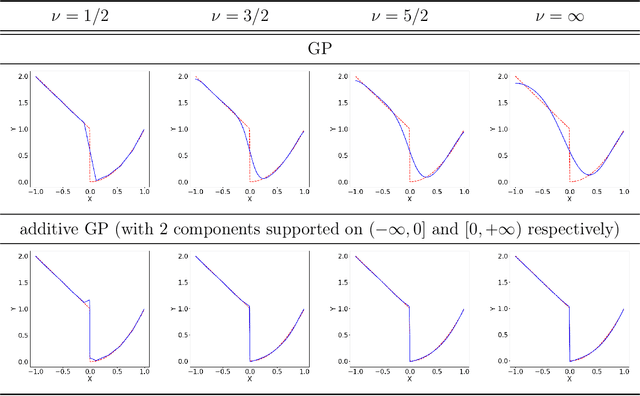
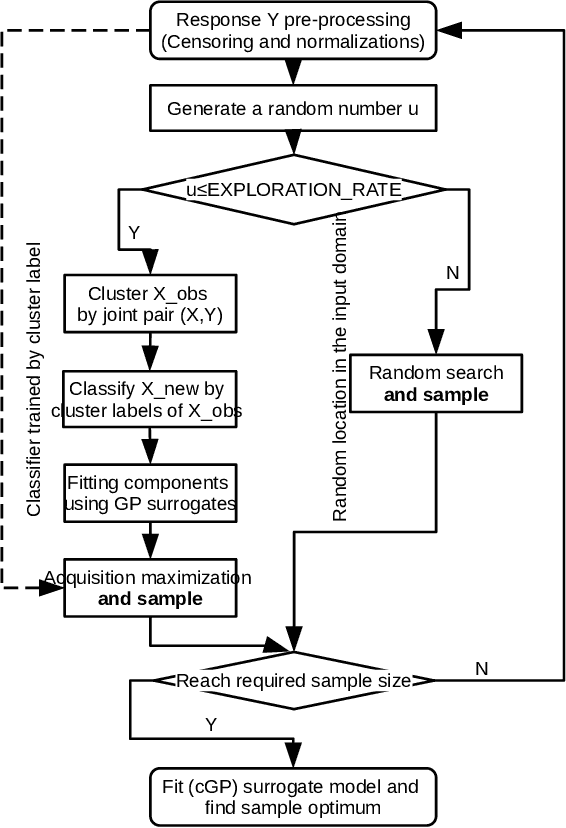
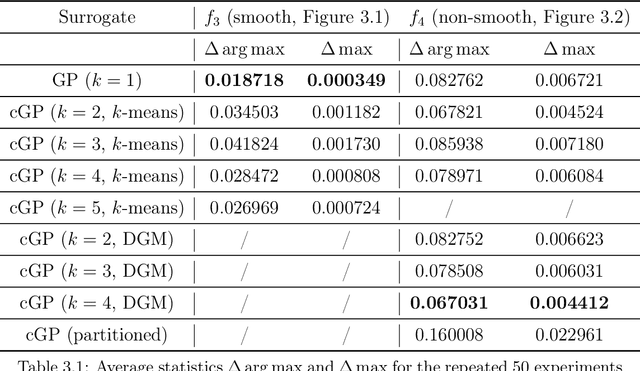
Building surrogate models is one common approach when we attempt to learn unknown black-box functions. Bayesian optimization provides a framework which allows us to build surrogate models based on sequential samples drawn from the function and find the optimum. Tuning algorithmic parameters to optimize the performance of large, complicated "black-box" application codes is a specific important application, which aims at finding the optima of black-box functions. Within the Bayesian optimization framework, the Gaussian process model produces smooth or continuous sample paths. However, the black-box function in the tuning problem is often non-smooth. This difficult tuning problem is worsened by the fact that we usually have limited sequential samples from the black-box function. Motivated by these issues encountered in tuning, we propose a novel additive Gaussian process model called clustered Gaussian process (cGP), where the additive components are induced by clustering. In the examples we studied, the performance can be improved by as much as 90% among repetitive experiments. By using this surrogate model, we want to capture the non-smoothness of the black-box function. In addition to an algorithm for constructing this model, we also apply the model to several artificial and real applications to evaluate it.

Multitask and Transfer Learning for Autotuning Exascale Applications

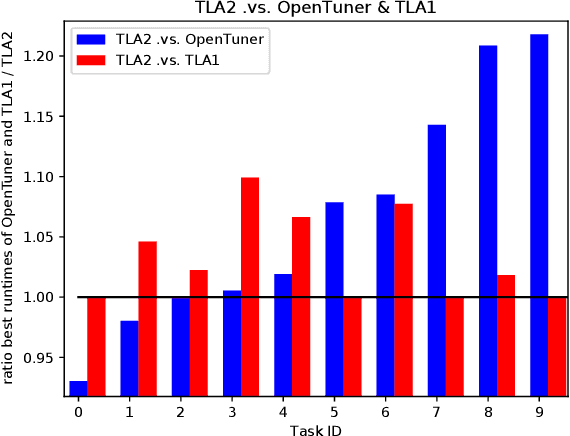
Multitask learning and transfer learning have proven to be useful in the field of machine learning when additional knowledge is available to help a prediction task. We aim at deriving methods following these paradigms for use in autotuning, where the goal is to find the optimal performance parameters of an application treated as a black-box function. We show comparative results with state-of-the-art autotuning techniques. For instance, we observe an average $1.5x$ improvement of the application runtime compared to the OpenTuner and HpBandSter autotuners. We explain how our approaches can be more suitable than some state-of-the-art autotuners for the tuning of any application in general and of expensive exascale applications in particular.

Efficient Online Hyperparameter Optimization for Kernel Ridge Regression with Applications to Traffic Time Series Prediction

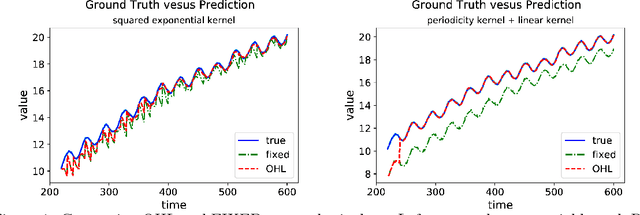
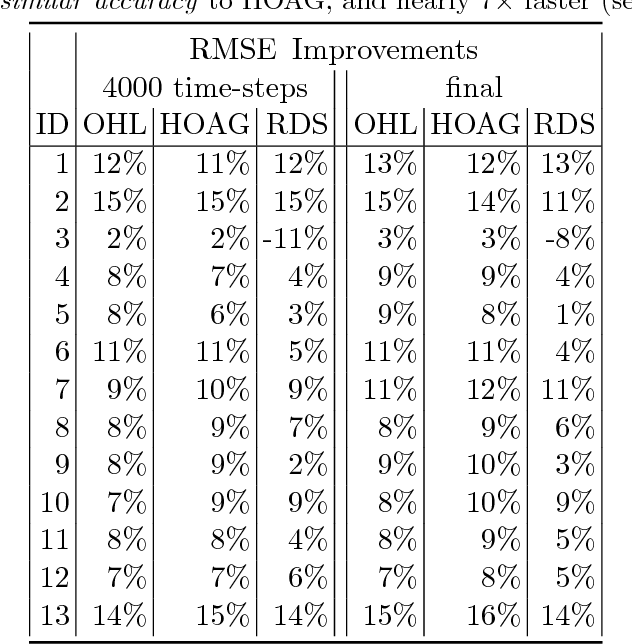
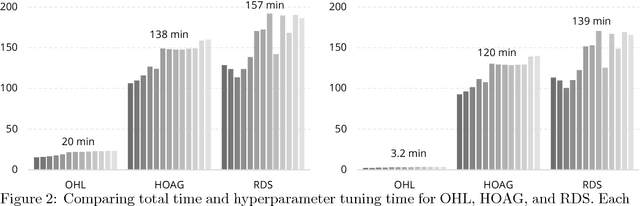
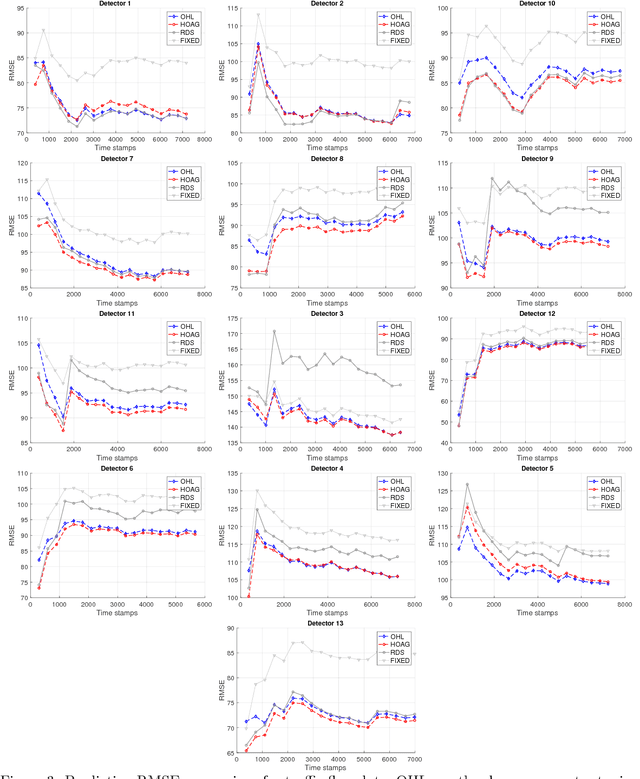
Computational efficiency is an important consideration for deploying machine learning models for time series prediction in an online setting. Machine learning algorithms adjust model parameters automatically based on the data, but often require users to set additional parameters, known as hyperparameters. Hyperparameters can significantly impact prediction accuracy. Traffic measurements, typically collected online by sensors, are serially correlated. Moreover, the data distribution may change gradually. A typical adaptation strategy is periodically re-tuning the model hyperparameters, at the cost of computational burden. In this work, we present an efficient and principled online hyperparameter optimization algorithm for Kernel Ridge regression applied to traffic prediction problems. In tests with real traffic measurement data, our approach requires as little as one-seventh of the computation time of other tuning methods, while achieving better or similar prediction accuracy.