PTQ4VM: Post-Training Quantization for Visual Mamba

Visual Mamba is an approach that extends the selective space state model, Mamba, to vision tasks. It processes image tokens sequentially in a fixed order, accumulating information to generate outputs. Despite its growing popularity for delivering high-quality outputs at a low computational cost across various tasks, Visual Mamba is highly susceptible to quantization, which makes further performance improvements challenging. Our analysis reveals that the fixed token access order in Visual Mamba introduces unique quantization challenges, which we categorize into three main issues: 1) token-wise variance, 2) channel-wise outliers, and 3) a long tail of activations. To address these challenges, we propose Post-Training Quantization for Visual Mamba (PTQ4VM), which introduces two key strategies: Per-Token Static (PTS) quantization and Joint Learning of Smoothing Scale and Step Size (JLSS). To the our best knowledge, this is the first quantization study on Visual Mamba. PTQ4VM can be applied to various Visual Mamba backbones, converting the pretrained model to a quantized format in under 15 minutes without notable quality degradation. Extensive experiments on large-scale classification and regression tasks demonstrate its effectiveness, achieving up to 1.83x speedup on GPUs with negligible accuracy loss compared to FP16. Our code is available at https://github.com/YoungHyun197/ptq4vm.

QEFT: Quantization for Efficient Fine-Tuning of LLMs

With the rapid growth in the use of fine-tuning for large language models (LLMs), optimizing fine-tuning while keeping inference efficient has become highly important. However, this is a challenging task as it requires improvements in all aspects, including inference speed, fine-tuning speed, memory consumption, and, most importantly, model quality. Previous studies have attempted to achieve this by combining quantization with fine-tuning, but they have failed to enhance all four aspects simultaneously. In this study, we propose a new lightweight technique called Quantization for Efficient Fine-Tuning (QEFT). QEFT accelerates both inference and fine-tuning, is supported by robust theoretical foundations, offers high flexibility, and maintains good hardware compatibility. Our extensive experiments demonstrate that QEFT matches the quality and versatility of full-precision parameter-efficient fine-tuning, while using fewer resources. Our code is available at https://github.com/xvyaward/qeft.

Surrogate-based Autotuning for Randomized Sketching Algorithms in Regression Problems

Algorithms from Randomized Numerical Linear Algebra (RandNLA) are known to be effective in handling high-dimensional computational problems, providing high-quality empirical performance as well as strong probabilistic guarantees. However, their practical application is complicated by the fact that the user needs to set various algorithm-specific tuning parameters which are different than those used in traditional NLA. This paper demonstrates how a surrogate-based autotuning approach can be used to address fundamental problems of parameter selection in RandNLA algorithms. In particular, we provide a detailed investigation of surrogate-based autotuning for sketch-and-precondition (SAP) based randomized least squares methods, which have been one of the great success stories in modern RandNLA. Empirical results show that our surrogate-based autotuning approach can achieve near-optimal performance with much less tuning cost than a random search (up to about 4x fewer trials of different parameter configurations). Moreover, while our experiments focus on least squares, our results demonstrate a general-purpose autotuning pipeline applicable to any kind of RandNLA algorithm.

Hybrid Models for Mixed Variables in Bayesian Optimization

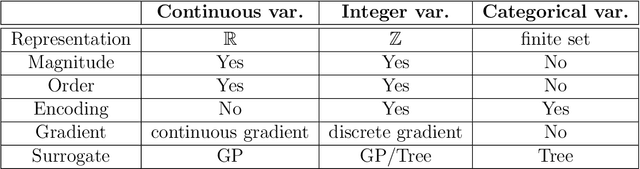
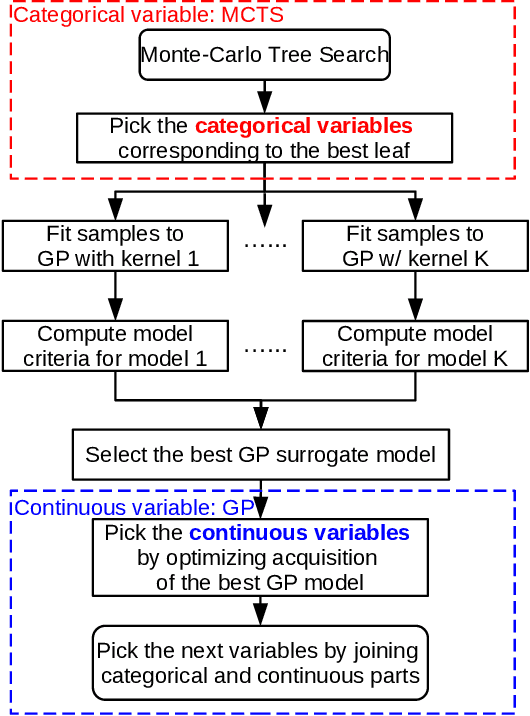
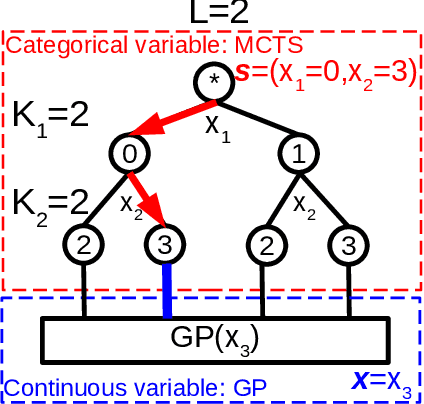
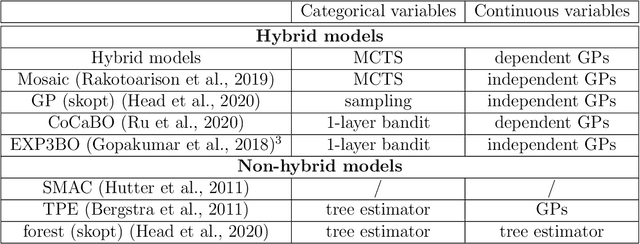
We systematically describe the problem of simultaneous surrogate modeling of mixed variables (i.e., continuous, integer and categorical variables) in the Bayesian optimization (BO) context. We provide a unified hybrid model using both Monte-Carlo tree search (MCTS) and Gaussian processes (GP) that encompasses and generalizes multiple state-of-the-art mixed BO surrogates. Based on the architecture, we propose applying a new dynamic model selection criterion among novel candidate families of covariance kernels, including non-stationary kernels and associated families. Different benchmark problems are studied and presented to support the superiority of our model, along with results highlighting the effectiveness of our method compared to most state-of-the-art mixed-variable methods in BO.

Non-smooth Bayesian Optimization in Tuning Problems

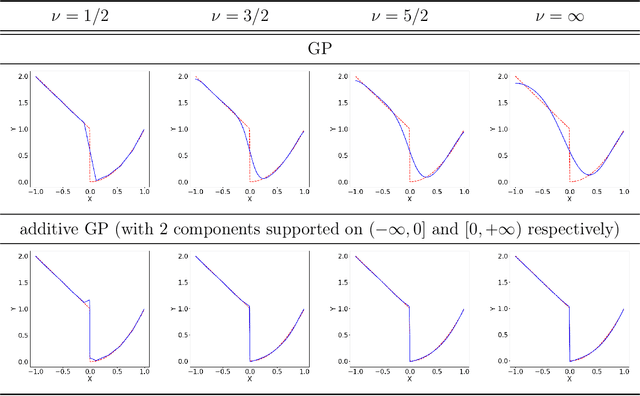
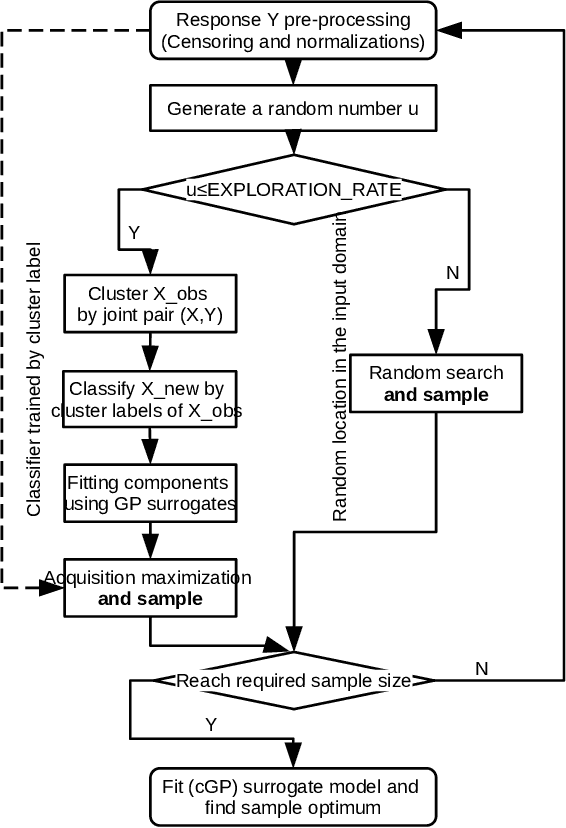
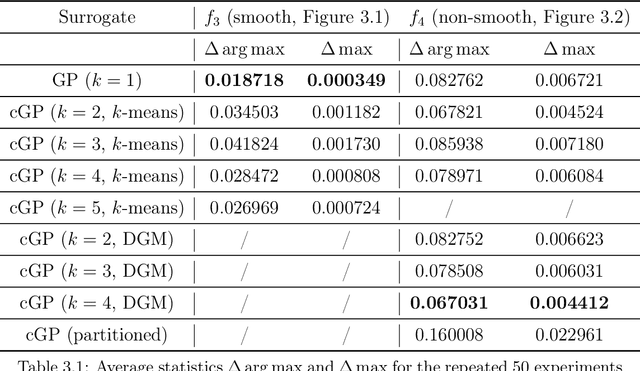
Building surrogate models is one common approach when we attempt to learn unknown black-box functions. Bayesian optimization provides a framework which allows us to build surrogate models based on sequential samples drawn from the function and find the optimum. Tuning algorithmic parameters to optimize the performance of large, complicated "black-box" application codes is a specific important application, which aims at finding the optima of black-box functions. Within the Bayesian optimization framework, the Gaussian process model produces smooth or continuous sample paths. However, the black-box function in the tuning problem is often non-smooth. This difficult tuning problem is worsened by the fact that we usually have limited sequential samples from the black-box function. Motivated by these issues encountered in tuning, we propose a novel additive Gaussian process model called clustered Gaussian process (cGP), where the additive components are induced by clustering. In the examples we studied, the performance can be improved by as much as 90% among repetitive experiments. By using this surrogate model, we want to capture the non-smoothness of the black-box function. In addition to an algorithm for constructing this model, we also apply the model to several artificial and real applications to evaluate it.