ResQ: A Novel Framework to Implement Residual Neural Networks on Analog Rydberg Atom Quantum Computers

Research in quantum machine learning has recently proliferated due to the potential of quantum computing to accelerate machine learning. An area of machine learning that has not yet been explored is neural ordinary differential equation (neural ODE) based residual neural networks (ResNets), which aim to improve the effectiveness of neural networks using the principles of ordinary differential equations. In this work, we present our insights about why analog Rydberg atom quantum computers are especially well-suited for ResNets. We also introduce ResQ, a novel framework to optimize the dynamics of Rydberg atom quantum computers to solve classification problems in machine learning using analog quantum neural ODEs.

EnQode: Fast Amplitude Embedding for Quantum Machine Learning Using Classical Data

Amplitude embedding (AE) is essential in quantum machine learning (QML) for encoding classical data onto quantum circuits. However, conventional AE methods suffer from deep, variable-length circuits that introduce high output error due to extensive gate usage and variable error rates across samples, resulting in noise-driven inconsistencies that degrade model accuracy. We introduce EnQode, a fast AE technique based on symbolic representation that addresses these limitations by clustering dataset samples and solving for cluster mean states through a low-depth, machine-specific ansatz. Optimized to reduce physical gates and SWAP operations, EnQode ensures all samples face consistent, low noise levels by standardizing circuit depth and composition. With over 90% fidelity in data mapping, EnQode enables robust, high-performance QML on noisy intermediate-scale quantum (NISQ) devices. Our open-source solution provides a scalable and efficient alternative for integrating classical data with quantum models.

Quantum EigenGame for excited state calculation

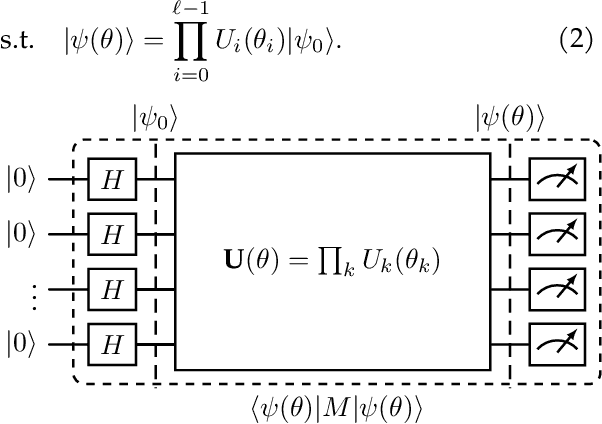
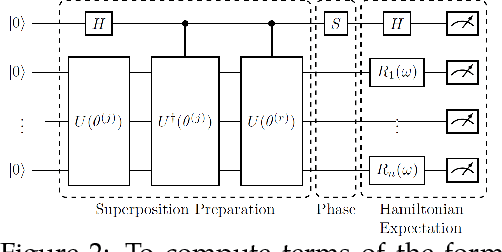
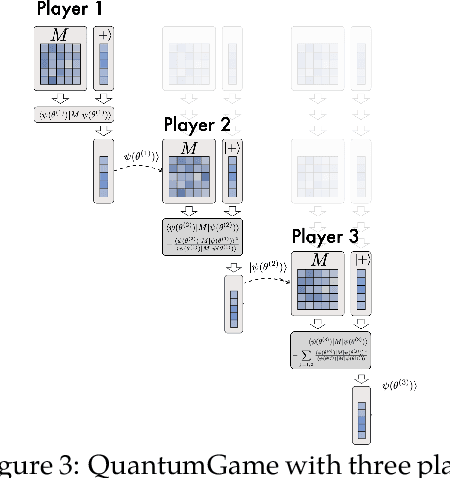
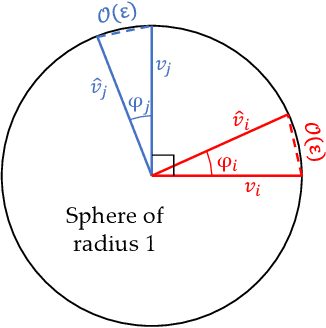
Computing the excited states of a given Hamiltonian is computationally hard for large systems, but methods that do so using quantum computers scale tractably. This problem is equivalent to the PCA problem where we are interested in decomposing a matrix into a collection of principal components. Classically, PCA is a well-studied problem setting, for which both centralized and distributed approaches have been developed. On the distributed side, one recent approach is that of EigenGame, a game-theoretic approach to finding eigenvectors where each eigenvector reaches a Nash equilibrium either sequentially or in parallel. With this work, we extend the EigenGame algorithm for both a $0^\text{th}$-order approach and for quantum computers, and harness the framework that quantum computing provides in computing excited states. Results show that using the Quantum EigenGame allows us to converge to excited states of a given Hamiltonian without the need of a deflation step. We also develop theory on error accumulation for finite-differences and parameterized approaches.