Quantum EigenGame for excited state calculation

Computing the excited states of a given Hamiltonian is computationally hard for large systems, but methods that do so using quantum computers scale tractably. This problem is equivalent to the PCA problem where we are interested in decomposing a matrix into a collection of principal components. Classically, PCA is a well-studied problem setting, for which both centralized and distributed approaches have been developed. On the distributed side, one recent approach is that of EigenGame, a game-theoretic approach to finding eigenvectors where each eigenvector reaches a Nash equilibrium either sequentially or in parallel. With this work, we extend the EigenGame algorithm for both a $0^\text{th}$-order approach and for quantum computers, and harness the framework that quantum computing provides in computing excited states. Results show that using the Quantum EigenGame allows us to converge to excited states of a given Hamiltonian without the need of a deflation step. We also develop theory on error accumulation for finite-differences and parameterized approaches.

Discriminating Quantum States with Quantum Machine Learning

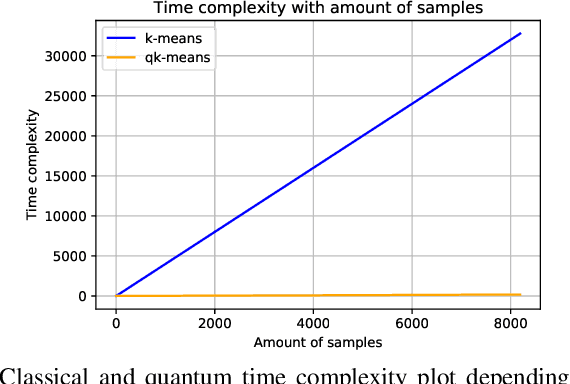
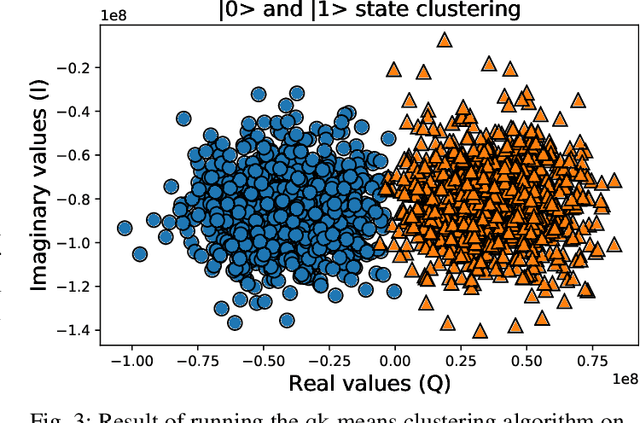
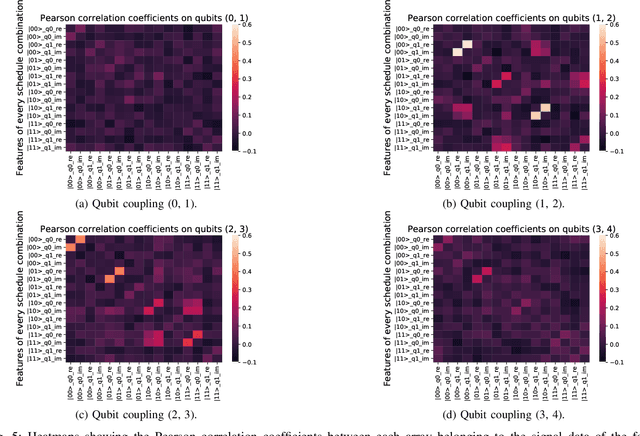
Quantum machine learning (QML) algorithms have obtained great relevance in the machine learning (ML) field due to the promise of quantum speedups when performing basic linear algebra subroutines (BLAS), a fundamental element in most ML algorithms. By making use of BLAS operations, we propose, implement and analyze a quantum k-means (qk-means) algorithm with a low time complexity of $\mathcal{O}(NKlog(D)I/C)$ to apply it to the fundamental problem of discriminating quantum states at readout. Discriminating quantum states allows the identification of quantum states $|0\rangle$ and $|1\rangle$ from low-level in-phase and quadrature signal (IQ) data, and can be done using custom ML models. In order to reduce dependency on a classical computer, we use the qk-means to perform state discrimination on the IBMQ Bogota device and managed to find assignment fidelities of up to 98.7% that were only marginally lower than that of the k-means algorithm. Inspection of assignment fidelity scores resulting from applying both algorithms to a combination of quantum states showed concordance to our correlation analysis using Pearson Correlation coefficients, where evidence shows cross-talk in the (1, 2) and (2, 3) neighboring qubit couples for the analyzed device.