Discriminating Quantum States with Quantum Machine Learning

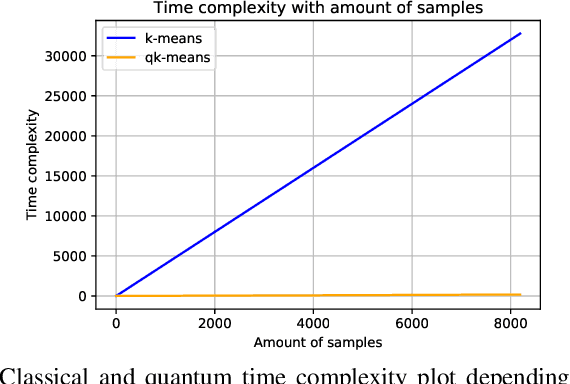
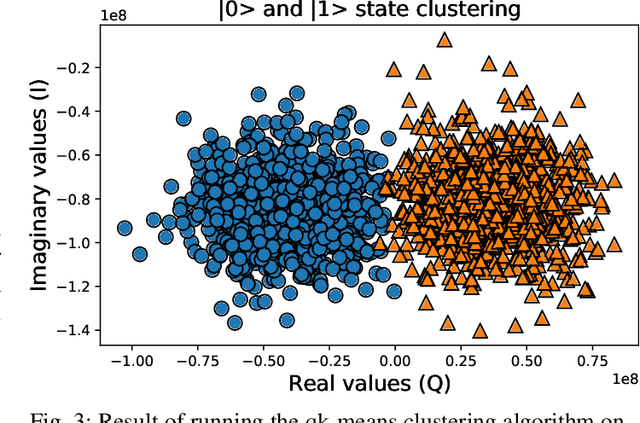
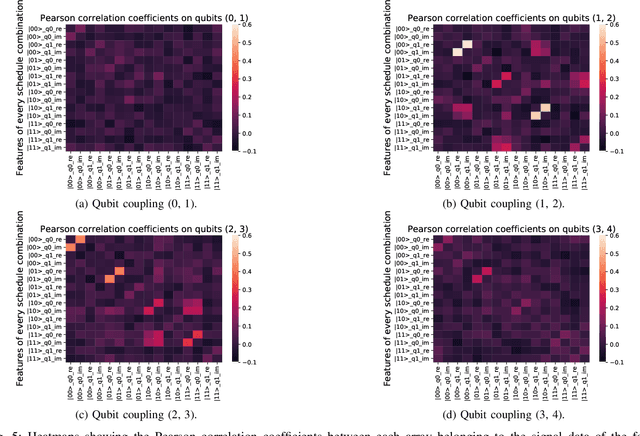
Quantum machine learning (QML) algorithms have obtained great relevance in the machine learning (ML) field due to the promise of quantum speedups when performing basic linear algebra subroutines (BLAS), a fundamental element in most ML algorithms. By making use of BLAS operations, we propose, implement and analyze a quantum k-means (qk-means) algorithm with a low time complexity of $\mathcal{O}(NKlog(D)I/C)$ to apply it to the fundamental problem of discriminating quantum states at readout. Discriminating quantum states allows the identification of quantum states $|0\rangle$ and $|1\rangle$ from low-level in-phase and quadrature signal (IQ) data, and can be done using custom ML models. In order to reduce dependency on a classical computer, we use the qk-means to perform state discrimination on the IBMQ Bogota device and managed to find assignment fidelities of up to 98.7% that were only marginally lower than that of the k-means algorithm. Inspection of assignment fidelity scores resulting from applying both algorithms to a combination of quantum states showed concordance to our correlation analysis using Pearson Correlation coefficients, where evidence shows cross-talk in the (1, 2) and (2, 3) neighboring qubit couples for the analyzed device.

Mode connectivity in the loss landscape of parameterized quantum circuits

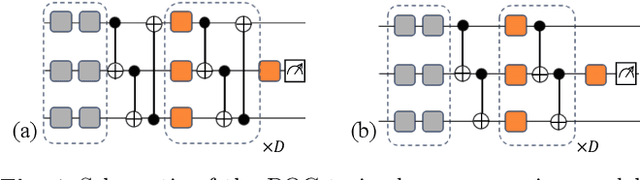
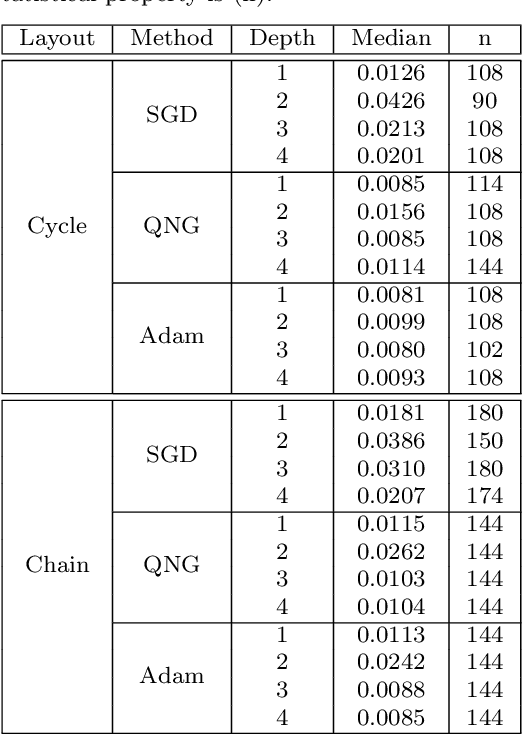
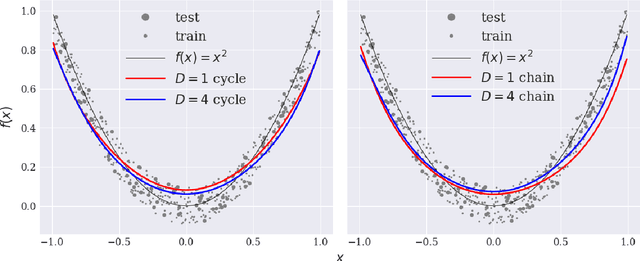
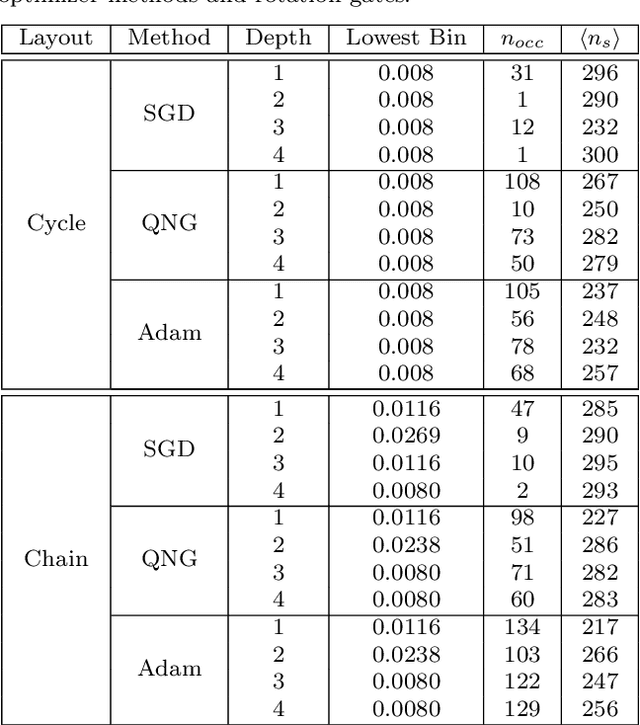
Variational training of parameterized quantum circuits (PQCs) underpins many workflows employed on near-term noisy intermediate scale quantum (NISQ) devices. It is a hybrid quantum-classical approach that minimizes an associated cost function in order to train a parameterized ansatz. In this paper we adapt the qualitative loss landscape characterization for neural networks introduced in \cite{goodfellow2014qualitatively,li2017visualizing} and tests for connectivity used in \cite{draxler2018essentially} to study the loss landscape features in PQC training. We present results for PQCs trained on a simple regression task, using the bilayer circuit ansatz, which consists of alternating layers of parameterized rotation gates and entangling gates. Multiple circuits are trained with $3$ different batch gradient optimizers: stochastic gradient descent, the quantum natural gradient, and Adam. We identify large features in the landscape that can lead to faster convergence in training workflows.