Emily Lynn
Mode connectivity in the loss landscape of parameterized quantum circuits
Nov 09, 2021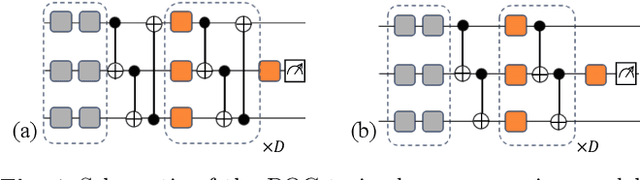
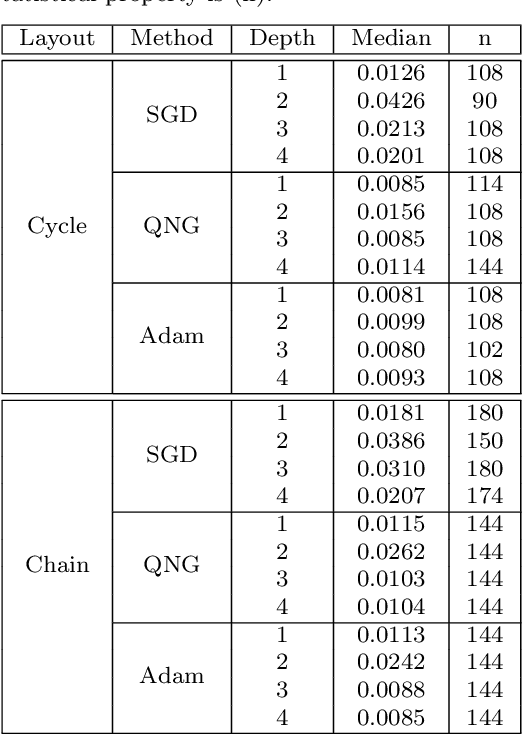
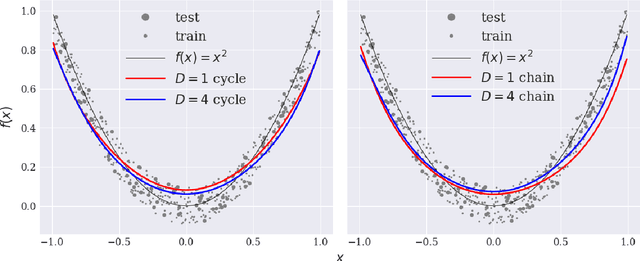
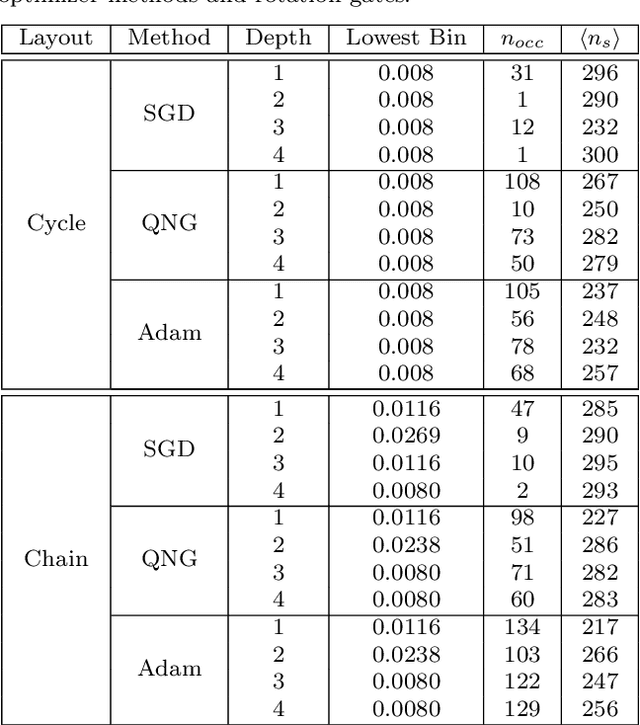
Abstract:Variational training of parameterized quantum circuits (PQCs) underpins many workflows employed on near-term noisy intermediate scale quantum (NISQ) devices. It is a hybrid quantum-classical approach that minimizes an associated cost function in order to train a parameterized ansatz. In this paper we adapt the qualitative loss landscape characterization for neural networks introduced in \cite{goodfellow2014qualitatively,li2017visualizing} and tests for connectivity used in \cite{draxler2018essentially} to study the loss landscape features in PQC training. We present results for PQCs trained on a simple regression task, using the bilayer circuit ansatz, which consists of alternating layers of parameterized rotation gates and entangling gates. Multiple circuits are trained with $3$ different batch gradient optimizers: stochastic gradient descent, the quantum natural gradient, and Adam. We identify large features in the landscape that can lead to faster convergence in training workflows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge