Mode connectivity in the loss landscape of parameterized quantum circuits

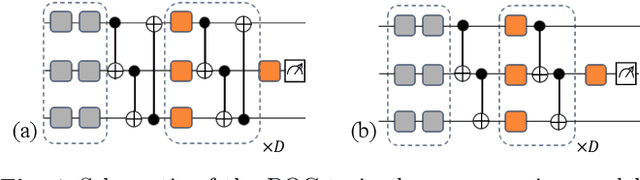
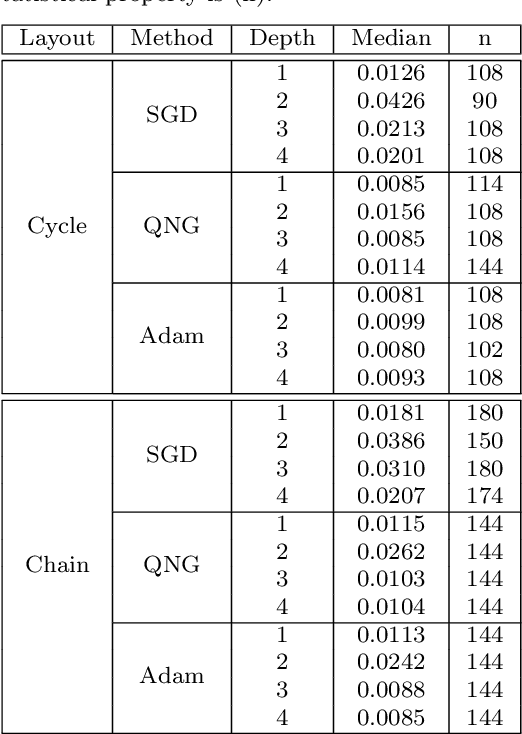
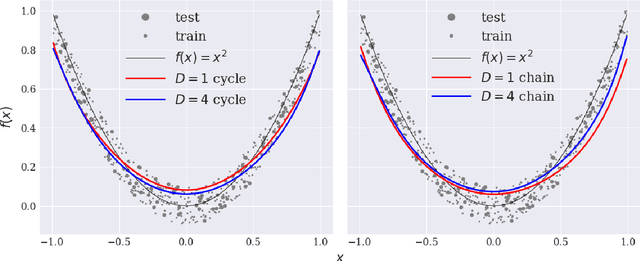
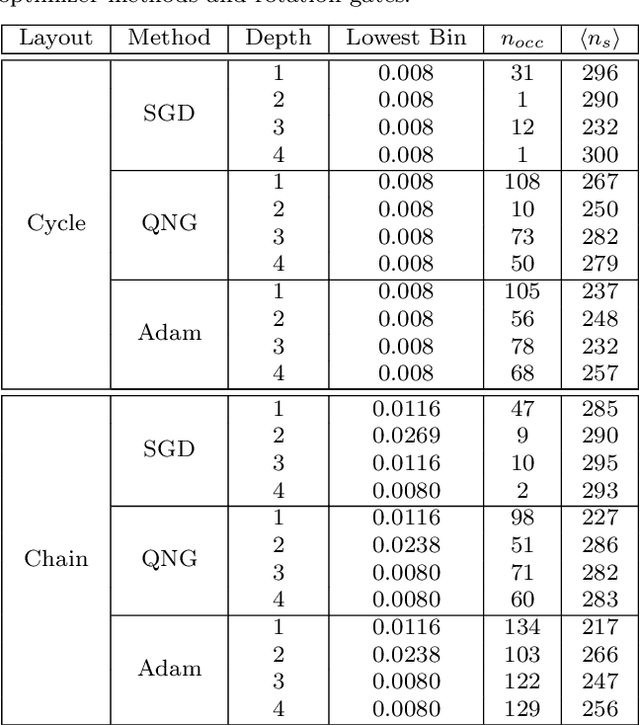
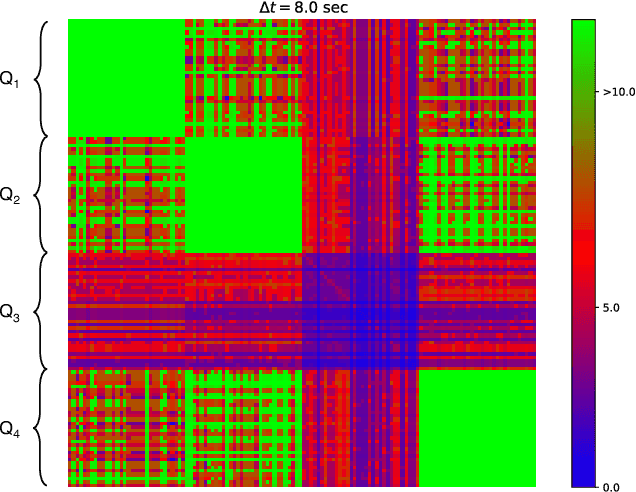
Variational training of parameterized quantum circuits (PQCs) underpins many workflows employed on near-term noisy intermediate scale quantum (NISQ) devices. It is a hybrid quantum-classical approach that minimizes an associated cost function in order to train a parameterized ansatz. In this paper we adapt the qualitative loss landscape characterization for neural networks introduced in \cite{goodfellow2014qualitatively,li2017visualizing} and tests for connectivity used in \cite{draxler2018essentially} to study the loss landscape features in PQC training. We present results for PQCs trained on a simple regression task, using the bilayer circuit ansatz, which consists of alternating layers of parameterized rotation gates and entangling gates. Multiple circuits are trained with $3$ different batch gradient optimizers: stochastic gradient descent, the quantum natural gradient, and Adam. We identify large features in the landscape that can lead to faster convergence in training workflows.

Spike-based primitives for graph algorithms

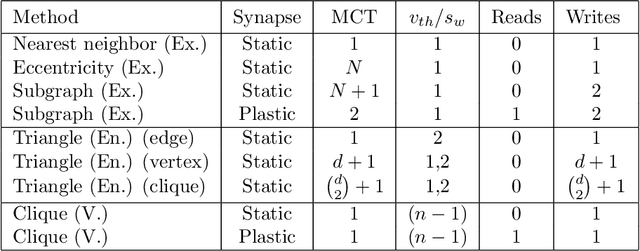
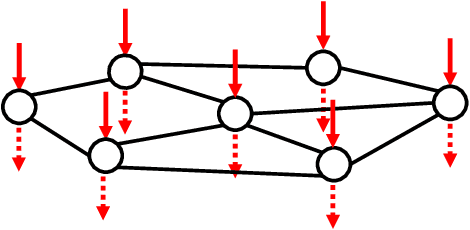
In this paper we consider graph algorithms and graphical analysis as a new application for neuromorphic computing platforms. We demonstrate how the nonlinear dynamics of spiking neurons can be used to implement low-level graph operations. Our results are hardware agnostic, and we present multiple versions of routines that can utilize static synapses or require synapse plasticity.

Community detection with spiking neural networks for neuromorphic hardware

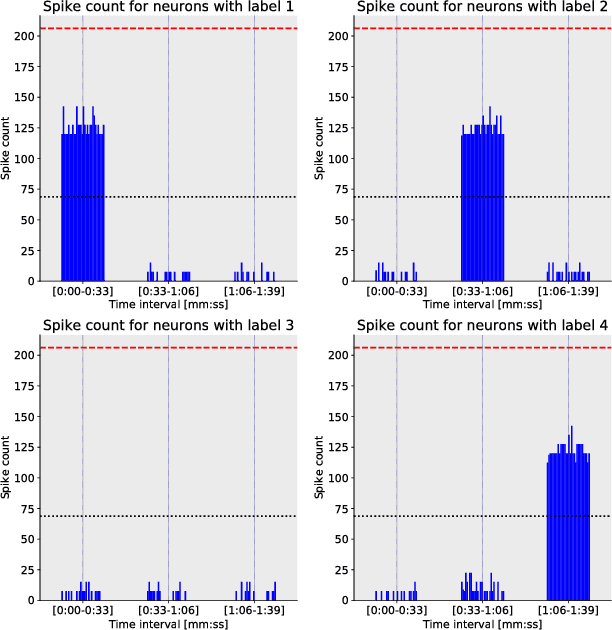
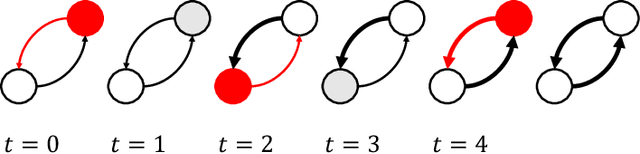
We present results related to the performance of an algorithm for community detection which incorporates event-driven computation. We define a mapping which takes a graph G to a system of spiking neurons. Using a fully connected spiking neuron system, with both inhibitory and excitatory synaptic connections, the firing patterns of neurons within the same community can be distinguished from firing patterns of neurons in different communities. On a random graph with 128 vertices and known community structure we show that by using binary decoding and a Hamming-distance based metric, individual communities can be identified from spike train similarities. Using bipolar decoding and finite rate thresholding, we verify that inhibitory connections prevent the spread of spiking patterns.