Adiabatic Quantum Support Vector Machines

Adiabatic quantum computers can solve difficult optimization problems (e.g., the quadratic unconstrained binary optimization problem), and they seem well suited to train machine learning models. In this paper, we describe an adiabatic quantum approach for training support vector machines. We show that the time complexity of our quantum approach is an order of magnitude better than the classical approach. Next, we compare the test accuracy of our quantum approach against a classical approach that uses the Scikit-learn library in Python across five benchmark datasets (Iris, Wisconsin Breast Cancer (WBC), Wine, Digits, and Lambeq). We show that our quantum approach obtains accuracies on par with the classical approach. Finally, we perform a scalability study in which we compute the total training times of the quantum approach and the classical approach with increasing number of features and number of data points in the training dataset. Our scalability results show that the quantum approach obtains a 3.5--4.5 times speedup over the classical approach on datasets with many (millions of) features.

On-Sensor Data Filtering using Neuromorphic Computing for High Energy Physics Experiments

This work describes the investigation of neuromorphic computing-based spiking neural network (SNN) models used to filter data from sensor electronics in high energy physics experiments conducted at the High Luminosity Large Hadron Collider. We present our approach for developing a compact neuromorphic model that filters out the sensor data based on the particle's transverse momentum with the goal of reducing the amount of data being sent to the downstream electronics. The incoming charge waveforms are converted to streams of binary-valued events, which are then processed by the SNN. We present our insights on the various system design choices - from data encoding to optimal hyperparameters of the training algorithm - for an accurate and compact SNN optimized for hardware deployment. Our results show that an SNN trained with an evolutionary algorithm and an optimized set of hyperparameters obtains a signal efficiency of about 91% with nearly half as many parameters as a deep neural network.

A Novel Spatial-Temporal Variational Quantum Circuit to Enable Deep Learning on NISQ Devices

Quantum computing presents a promising approach for machine learning with its capability for extremely parallel computation in high-dimension through superposition and entanglement. Despite its potential, existing quantum learning algorithms, such as Variational Quantum Circuits(VQCs), face challenges in handling more complex datasets, particularly those that are not linearly separable. What's more, it encounters the deployability issue, making the learning models suffer a drastic accuracy drop after deploying them to the actual quantum devices. To overcome these limitations, this paper proposes a novel spatial-temporal design, namely ST-VQC, to integrate non-linearity in quantum learning and improve the robustness of the learning model to noise. Specifically, ST-VQC can extract spatial features via a novel block-based encoding quantum sub-circuit coupled with a layer-wise computation quantum sub-circuit to enable temporal-wise deep learning. Additionally, a SWAP-Free physical circuit design is devised to improve robustness. These designs bring a number of hyperparameters. After a systematic analysis of the design space for each design component, an automated optimization framework is proposed to generate the ST-VQC quantum circuit. The proposed ST-VQC has been evaluated on two IBM quantum processors, ibm_cairo with 27 qubits and ibmq_lima with 7 qubits to assess its effectiveness. The results of the evaluation on the standard dataset for binary classification show that ST-VQC can achieve over 30% accuracy improvement compared with existing VQCs on actual quantum computers. Moreover, on a non-linear synthetic dataset, the ST-VQC outperforms a linear classifier by 27.9%, while the linear classifier using classical computing outperforms the existing VQC by 15.58%.

SuperNeuro: A Fast and Scalable Simulator for Neuromorphic Computing

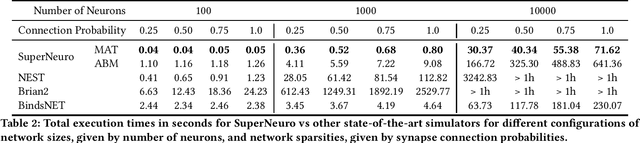
In many neuromorphic workflows, simulators play a vital role for important tasks such as training spiking neural networks (SNNs), running neuroscience simulations, and designing, implementing and testing neuromorphic algorithms. Currently available simulators are catered to either neuroscience workflows (such as NEST and Brian2) or deep learning workflows (such as BindsNET). While the neuroscience-based simulators are slow and not very scalable, the deep learning-based simulators do not support certain functionalities such as synaptic delay that are typical of neuromorphic workloads. In this paper, we address this gap in the literature and present SuperNeuro, which is a fast and scalable simulator for neuromorphic computing, capable of both homogeneous and heterogeneous simulations as well as GPU acceleration. We also present preliminary results comparing SuperNeuro to widely used neuromorphic simulators such as NEST, Brian2 and BindsNET in terms of computation times. We demonstrate that SuperNeuro can be approximately 10--300 times faster than some of the other simulators for small sparse networks. On large sparse and large dense networks, SuperNeuro can be approximately 2.2 and 3.4 times faster than the other simulators respectively.

Encoding Integers and Rationals on Neuromorphic Computers using Virtual Neuron

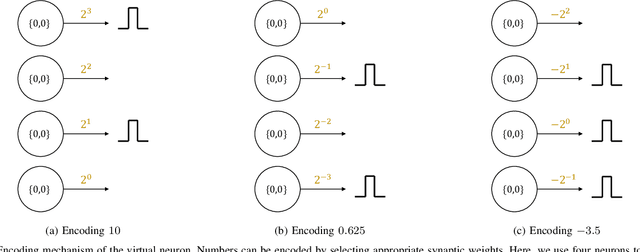
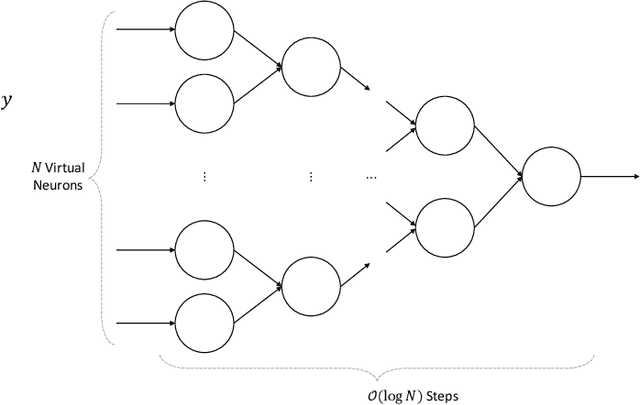
Neuromorphic computers perform computations by emulating the human brain, and use extremely low power. They are expected to be indispensable for energy-efficient computing in the future. While they are primarily used in spiking neural network-based machine learning applications, neuromorphic computers are known to be Turing-complete, and thus, capable of general-purpose computation. However, to fully realize their potential for general-purpose, energy-efficient computing, it is important to devise efficient mechanisms for encoding numbers. Current encoding approaches have limited applicability and may not be suitable for general-purpose computation. In this paper, we present the virtual neuron as an encoding mechanism for integers and rational numbers. We evaluate the performance of the virtual neuron on physical and simulated neuromorphic hardware and show that it can perform an addition operation using 23 nJ of energy on average using a mixed-signal memristor-based neuromorphic processor. We also demonstrate its utility by using it in some of the mu-recursive functions, which are the building blocks of general-purpose computation.

A Hybrid Quantum-Classical Neural Network Architecture for Binary Classification

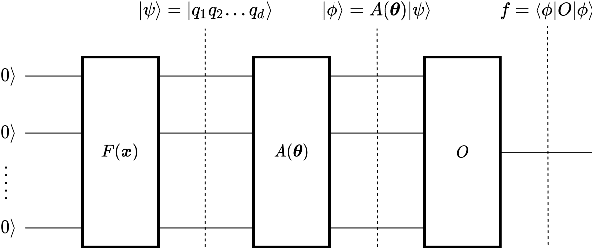
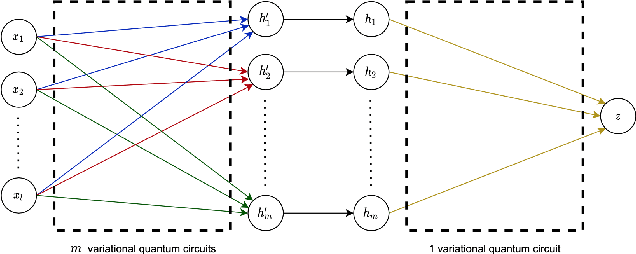
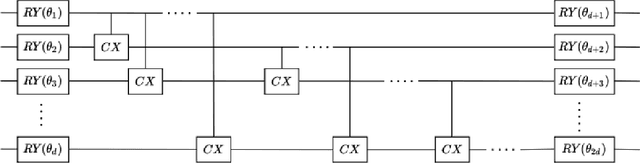
Deep learning is one of the most successful and far-reaching strategies used in machine learning today. However, the scale and utility of neural networks is still greatly limited by the current hardware used to train them. These concerns have become increasingly pressing as conventional computers quickly approach physical limitations that will slow performance improvements in years to come. For these reasons, scientists have begun to explore alternative computing platforms, like quantum computers, for training neural networks. In recent years, variational quantum circuits have emerged as one of the most successful approaches to quantum deep learning on noisy intermediate scale quantum devices. We propose a hybrid quantum-classical neural network architecture where each neuron is a variational quantum circuit. We empirically analyze the performance of this hybrid neural network on a series of binary classification data sets using a simulated universal quantum computer and a state of the art universal quantum computer. On simulated hardware, we observe that the hybrid neural network achieves roughly 10% higher classification accuracy and 20% better minimization of cost than an individual variational quantum circuit. On quantum hardware, we observe that each model only performs well when the qubit and gate count is sufficiently small.

Discriminating Quantum States with Quantum Machine Learning

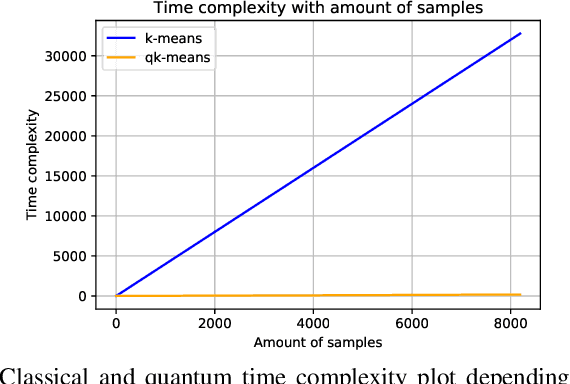
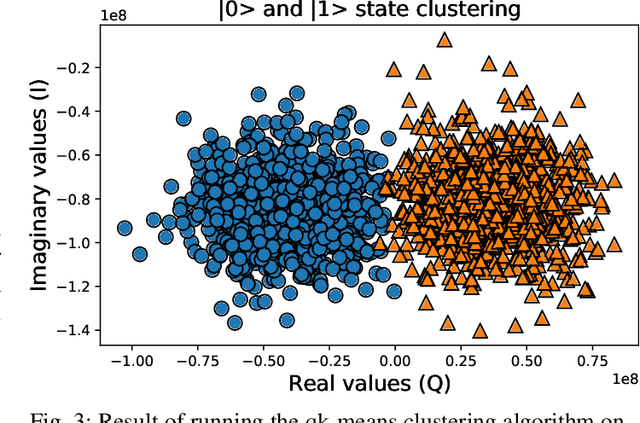
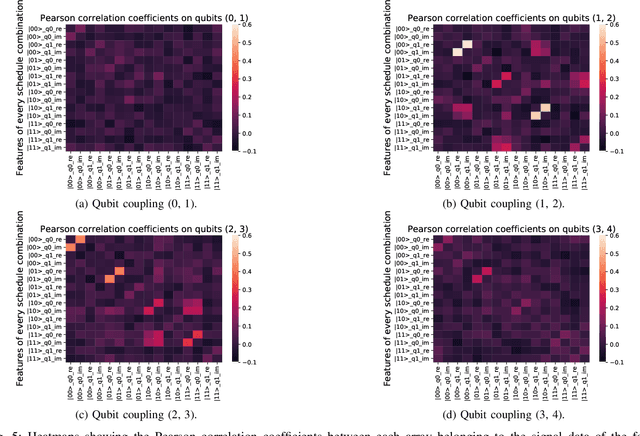
Quantum machine learning (QML) algorithms have obtained great relevance in the machine learning (ML) field due to the promise of quantum speedups when performing basic linear algebra subroutines (BLAS), a fundamental element in most ML algorithms. By making use of BLAS operations, we propose, implement and analyze a quantum k-means (qk-means) algorithm with a low time complexity of $\mathcal{O}(NKlog(D)I/C)$ to apply it to the fundamental problem of discriminating quantum states at readout. Discriminating quantum states allows the identification of quantum states $|0\rangle$ and $|1\rangle$ from low-level in-phase and quadrature signal (IQ) data, and can be done using custom ML models. In order to reduce dependency on a classical computer, we use the qk-means to perform state discrimination on the IBMQ Bogota device and managed to find assignment fidelities of up to 98.7% that were only marginally lower than that of the k-means algorithm. Inspection of assignment fidelity scores resulting from applying both algorithms to a combination of quantum states showed concordance to our correlation analysis using Pearson Correlation coefficients, where evidence shows cross-talk in the (1, 2) and (2, 3) neighboring qubit couples for the analyzed device.

Neuromorphic Computing is Turing-Complete

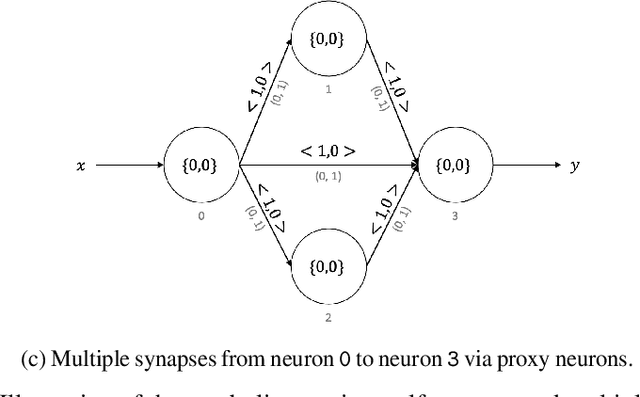
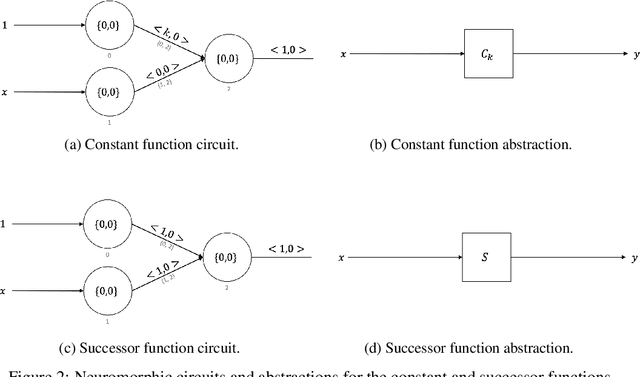
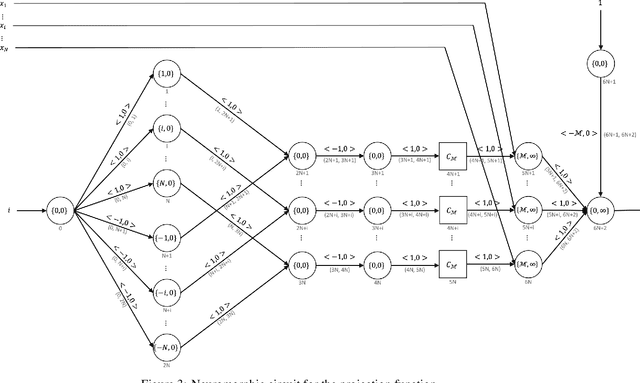
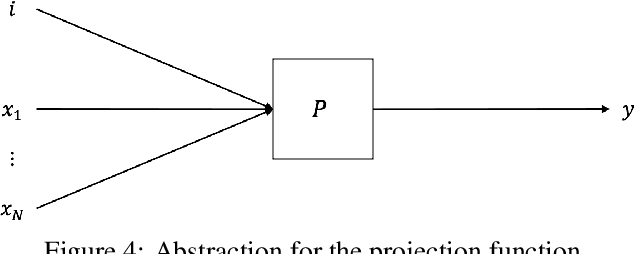
Neuromorphic computing is a non-von Neumann computing paradigm that performs computation by emulating the human brain. Neuromorphic systems are extremely energy-efficient and known to consume thousands of times less power than CPUs and GPUs. They have the potential to drive critical use cases such as autonomous vehicles, edge computing and internet of things in the future. For this reason, they are sought to be an indispensable part of the future computing landscape. Neuromorphic systems are mainly used for spike-based machine learning applications, although there are some non-machine learning applications in graph theory, differential equations, and spike-based simulations. These applications suggest that neuromorphic computing might be capable of general-purpose computing. However, general-purpose computability of neuromorphic computing has not been established yet. In this work, we prove that neuromorphic computing is Turing-complete and therefore capable of general-purpose computing. Specifically, we present a model of neuromorphic computing, with just two neuron parameters (threshold and leak), and two synaptic parameters (weight and delay). We devise neuromorphic circuits for computing all the {\mu}-recursive functions (i.e., constant, successor and projection functions) and all the {\mu}-recursive operators (i.e., composition, primitive recursion and minimization operators). Given that the {\mu}-recursive functions and operators are precisely the ones that can be computed using a Turing machine, this work establishes the Turing-completeness of neuromorphic computing.

Quantum Discriminator for Binary Classification

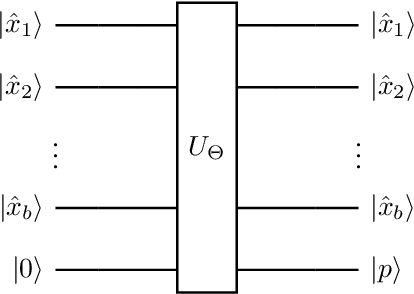
Quantum computers operate in the high-dimensional tensor product spaces and are known to outperform classical computers on many problems. They are poised to accelerate machine learning tasks in the future. In this work, we operate in the quantum machine learning (QML) regime where a QML model is trained using a quantum-classical hybrid algorithm and inferencing is performed using a quantum algorithm. We leverage the traditional two-step machine learning workflow, where features are extracted from the data in the first step and a discriminator acting on the extracted features is used to classify the data in the second step. Assuming that the binary features have been extracted from the data, we propose a quantum discriminator for binary classification. The quantum discriminator takes as input the binary features of a data point and a prediction qubit in the zero state, and outputs the correct class of the data point. The quantum discriminator is defined by a parameterized unitary matrix $U_\Theta$ containing $\mathcal{O}(N)$ parameters, where $N$ is the number of data points in the training data set. Furthermore, we show that the quantum discriminator can be trained in $\mathcal{O}(N \log N)$ time using $\mathcal{O}(N \log N)$ classical bits and $\mathcal{O}(\log N)$ qubits. We also show that inferencing for the quantum discriminator can be done in $\mathcal{O}(N)$ time using $\mathcal{O}(\log N)$ qubits. Finally, we use the quantum discriminator to classify the XOR problem on the IBM Q universal quantum computer with $100\%$ accuracy.