A Hybrid Quantum-Classical Neural Network Architecture for Binary Classification

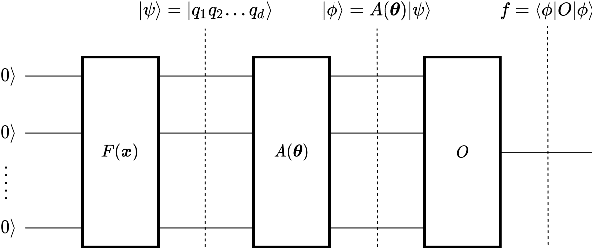
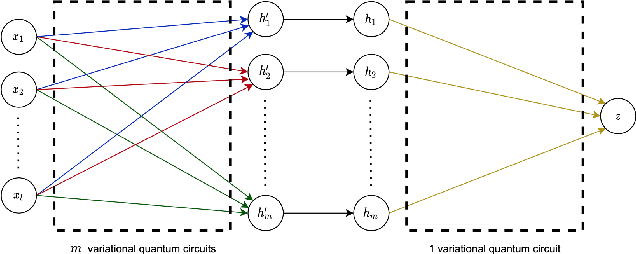
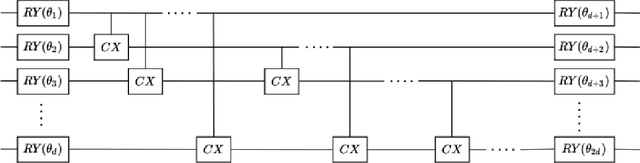
Deep learning is one of the most successful and far-reaching strategies used in machine learning today. However, the scale and utility of neural networks is still greatly limited by the current hardware used to train them. These concerns have become increasingly pressing as conventional computers quickly approach physical limitations that will slow performance improvements in years to come. For these reasons, scientists have begun to explore alternative computing platforms, like quantum computers, for training neural networks. In recent years, variational quantum circuits have emerged as one of the most successful approaches to quantum deep learning on noisy intermediate scale quantum devices. We propose a hybrid quantum-classical neural network architecture where each neuron is a variational quantum circuit. We empirically analyze the performance of this hybrid neural network on a series of binary classification data sets using a simulated universal quantum computer and a state of the art universal quantum computer. On simulated hardware, we observe that the hybrid neural network achieves roughly 10% higher classification accuracy and 20% better minimization of cost than an individual variational quantum circuit. On quantum hardware, we observe that each model only performs well when the qubit and gate count is sufficiently small.

Balanced k-Means Clustering on an Adiabatic Quantum Computer

Adiabatic quantum computers are a promising platform for approximately solving challenging optimization problems. We present a quantum approach to solving the balanced $k$-means clustering training problem on the D-Wave 2000Q adiabatic quantum computer. Existing classical approaches scale poorly for large datasets and only guarantee a locally optimal solution. We show that our quantum approach better targets the global solution of the training problem, while achieving better theoretic scalability on large datasets. We test our quantum approach on a number of small problems, and observe clustering performance similar to the best classical algorithms.

QUBO Formulations for Training Machine Learning Models

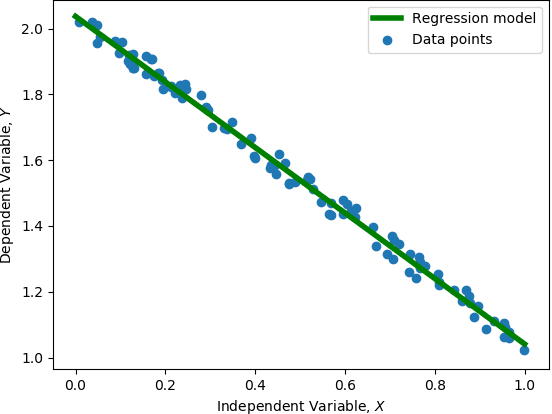
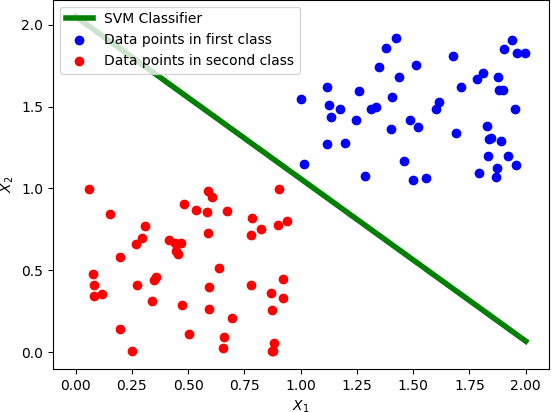
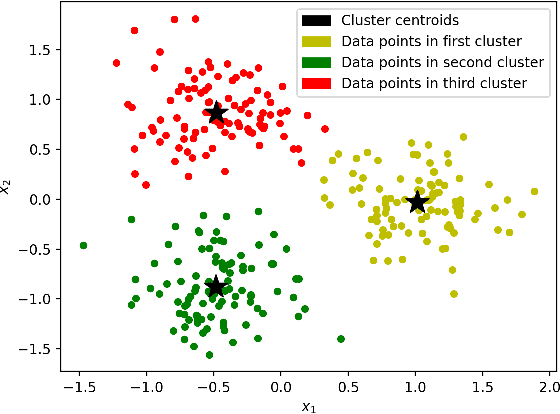
Training machine learning models on classical computers is usually a time and compute intensive process. With Moore's law coming to an end and ever increasing demand for large-scale data analysis using machine learning, we must leverage non-conventional computing paradigms like quantum computing to train machine learning models efficiently. Adiabatic quantum computers like the D-Wave 2000Q can approximately solve NP-hard optimization problems, such as the quadratic unconstrained binary optimization (QUBO), faster than classical computers. Since many machine learning problems are also NP-hard, we believe adiabatic quantum computers might be instrumental in training machine learning models efficiently in the post Moore's law era. In order to solve a problem on adiabatic quantum computers, it must be formulated as a QUBO problem, which is a challenging task in itself. In this paper, we formulate the training problems of three machine learning models---linear regression, support vector machine (SVM) and equal-sized k-means clustering---as QUBO problems so that they can be trained on adiabatic quantum computers efficiently. We also analyze the time and space complexities of our formulations and compare them to the state-of-the-art classical algorithms for training these machine learning models. We show that the time and space complexities of our formulations are better (in the case of SVM and equal-sized k-means clustering) or equivalent (in case of linear regression) to their classical counterparts.