Adiabatic Quantum Optimization Fails to Solve the Knapsack Problem

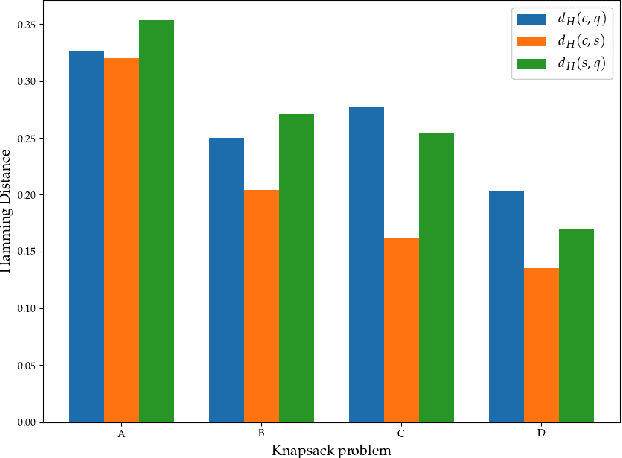
In this work, we attempt to solve the integer-weight knapsack problem using the D-Wave 2000Q adiabatic quantum computer. The knapsack problem is a well-known NP-complete problem in computer science, with applications in economics, business, finance, etc. We attempt to solve a number of small knapsack problems whose optimal solutions are known; we find that adiabatic quantum optimization fails to produce solutions corresponding to optimal filling of the knapsack in all problem instances. We compare results obtained on the quantum hardware to the classical simulated annealing algorithm and two solvers employing a hybrid branch-and-bound algorithm. The simulated annealing algorithm also fails to produce the optimal filling of the knapsack, though solutions obtained by simulated and quantum annealing are no more similar to each other than to the correct solution. We discuss potential causes for this observed failure of adiabatic quantum optimization.

QUBO Formulations for Training Machine Learning Models

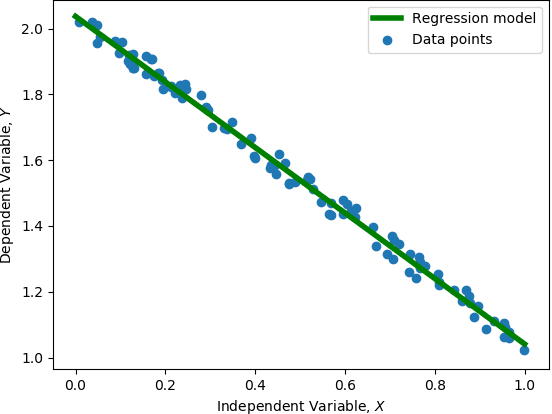
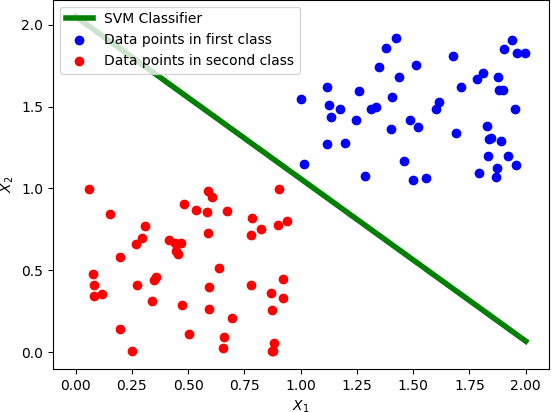
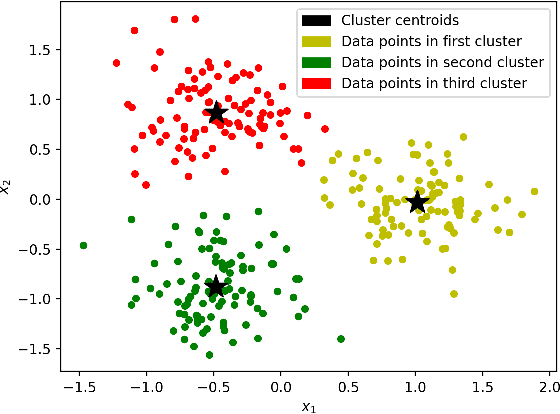
Training machine learning models on classical computers is usually a time and compute intensive process. With Moore's law coming to an end and ever increasing demand for large-scale data analysis using machine learning, we must leverage non-conventional computing paradigms like quantum computing to train machine learning models efficiently. Adiabatic quantum computers like the D-Wave 2000Q can approximately solve NP-hard optimization problems, such as the quadratic unconstrained binary optimization (QUBO), faster than classical computers. Since many machine learning problems are also NP-hard, we believe adiabatic quantum computers might be instrumental in training machine learning models efficiently in the post Moore's law era. In order to solve a problem on adiabatic quantum computers, it must be formulated as a QUBO problem, which is a challenging task in itself. In this paper, we formulate the training problems of three machine learning models---linear regression, support vector machine (SVM) and equal-sized k-means clustering---as QUBO problems so that they can be trained on adiabatic quantum computers efficiently. We also analyze the time and space complexities of our formulations and compare them to the state-of-the-art classical algorithms for training these machine learning models. We show that the time and space complexities of our formulations are better (in the case of SVM and equal-sized k-means clustering) or equivalent (in case of linear regression) to their classical counterparts.