A Novel Spatial-Temporal Variational Quantum Circuit to Enable Deep Learning on NISQ Devices

Quantum computing presents a promising approach for machine learning with its capability for extremely parallel computation in high-dimension through superposition and entanglement. Despite its potential, existing quantum learning algorithms, such as Variational Quantum Circuits(VQCs), face challenges in handling more complex datasets, particularly those that are not linearly separable. What's more, it encounters the deployability issue, making the learning models suffer a drastic accuracy drop after deploying them to the actual quantum devices. To overcome these limitations, this paper proposes a novel spatial-temporal design, namely ST-VQC, to integrate non-linearity in quantum learning and improve the robustness of the learning model to noise. Specifically, ST-VQC can extract spatial features via a novel block-based encoding quantum sub-circuit coupled with a layer-wise computation quantum sub-circuit to enable temporal-wise deep learning. Additionally, a SWAP-Free physical circuit design is devised to improve robustness. These designs bring a number of hyperparameters. After a systematic analysis of the design space for each design component, an automated optimization framework is proposed to generate the ST-VQC quantum circuit. The proposed ST-VQC has been evaluated on two IBM quantum processors, ibm_cairo with 27 qubits and ibmq_lima with 7 qubits to assess its effectiveness. The results of the evaluation on the standard dataset for binary classification show that ST-VQC can achieve over 30% accuracy improvement compared with existing VQCs on actual quantum computers. Moreover, on a non-linear synthetic dataset, the ST-VQC outperforms a linear classifier by 27.9%, while the linear classifier using classical computing outperforms the existing VQC by 15.58%.

QuMoS: A Framework for Preserving Security of Quantum Machine Learning Model

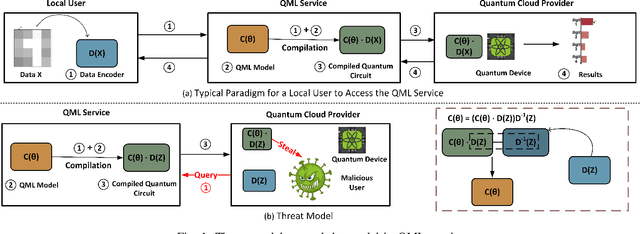
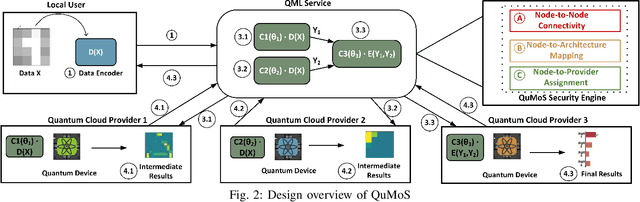
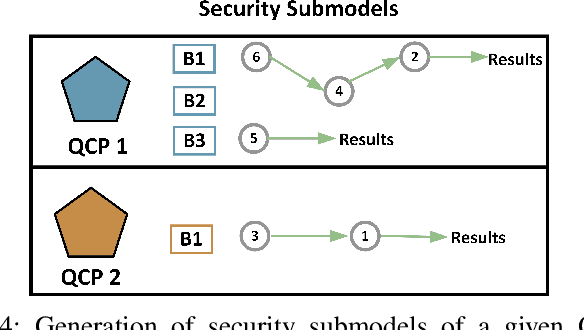
Security has always been a critical issue in machine learning (ML) applications. Due to the high cost of model training -- such as collecting relevant samples, labeling data, and consuming computing power -- model-stealing attack is one of the most fundamental but vitally important issues. When it comes to quantum computing, such a quantum machine learning (QML) model-stealing attack also exists and it is even more severe because the traditional encryption method can hardly be directly applied to quantum computation. On the other hand, due to the limited quantum computing resources, the monetary cost of training QML model can be even higher than classical ones in the near term. Therefore, a well-tuned QML model developed by a company can be delegated to a quantum cloud provider as a service to be used by ordinary users. In this case, the QML model will be leaked if the cloud provider is under attack. To address such a problem, we propose a novel framework, namely QuMoS, to preserve model security. Instead of applying encryption algorithms, we propose to distribute the QML model to multiple physically isolated quantum cloud providers. As such, even if the adversary in one provider can obtain a partial model, the information of the full model is maintained in the QML service company. Although promising, we observed an arbitrary model design under distributed settings cannot provide model security. We further developed a reinforcement learning-based security engine, which can automatically optimize the model design under the distributed setting, such that a good trade-off between model performance and security can be made. Experimental results on four datasets show that the model design proposed by QuMoS can achieve a close accuracy to the model designed with neural architecture search under centralized settings while providing the highest security than the baselines.

Quantum Neural Network Compression

Model compression, such as pruning and quantization, has been widely applied to optimize neural networks on resource-limited classical devices. Recently, there are growing interest in variational quantum circuits (VQC), that is, a type of neural network on quantum computers (a.k.a., quantum neural networks). It is well known that the near-term quantum devices have high noise and limited resources (i.e., quantum bits, qubits); yet, how to compress quantum neural networks has not been thoroughly studied. One might think it is straightforward to apply the classical compression techniques to quantum scenarios. However, this paper reveals that there exist differences between the compression of quantum and classical neural networks. Based on our observations, we claim that the compilation/traspilation has to be involved in the compression process. On top of this, we propose the very first systematical framework, namely CompVQC, to compress quantum neural networks (QNNs).In CompVQC, the key component is a novel compression algorithm, which is based on the alternating direction method of multipliers (ADMM) approach. Experiments demonstrate the advantage of the CompVQC, reducing the circuit depth (almost over 2.5 %) with a negligible accuracy drop (<1%), which outperforms other competitors. Another promising truth is our CompVQC can indeed promote the robustness of the QNN on the near-term noisy quantum devices.

Measurement error models: from nonparametric methods to deep neural networks

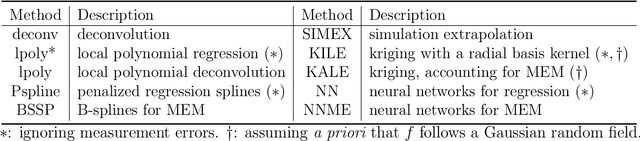
The success of deep learning has inspired recent interests in applying neural networks in statistical inference. In this paper, we investigate the use of deep neural networks for nonparametric regression with measurement errors. We propose an efficient neural network design for estimating measurement error models, in which we use a fully connected feed-forward neural network (FNN) to approximate the regression function $f(x)$, a normalizing flow to approximate the prior distribution of $X$, and an inference network to approximate the posterior distribution of $X$. Our method utilizes recent advances in variational inference for deep neural networks, such as the importance weight autoencoder, doubly reparametrized gradient estimator, and non-linear independent components estimation. We conduct an extensive numerical study to compare the neural network approach with classical nonparametric methods and observe that the neural network approach is more flexible in accommodating different classes of regression functions and performs superior or comparable to the best available method in nearly all settings.