A Comparison of DeepSeek and Other LLMs

Recently, DeepSeek has been the focus of attention in and beyond the AI community. An interesting problem is how DeepSeek compares to other large language models (LLMs). There are many tasks an LLM can do, and in this paper, we use the task of predicting an outcome using a short text for comparison. We consider two settings, an authorship classification setting and a citation classification setting. In the first one, the goal is to determine whether a short text is written by human or AI. In the second one, the goal is to classify a citation to one of four types using the textual content. For each experiment, we compare DeepSeek with $4$ popular LLMs: Claude, Gemini, GPT, and Llama. We find that, in terms of classification accuracy, DeepSeek outperforms Gemini, GPT, and Llama in most cases, but underperforms Claude. We also find that DeepSeek is comparably slower than others but with a low cost to use, while Claude is much more expensive than all the others. Finally, we find that in terms of similarity, the output of DeepSeek is most similar to those of Gemini and Claude (and among all $5$ LLMs, Claude and Gemini have the most similar outputs). In this paper, we also present a fully-labeled dataset collected by ourselves, and propose a recipe where we can use the LLMs and a recent data set, MADStat, to generate new data sets. The datasets in our paper can be used as benchmarks for future study on LLMs.

Improved Algorithm and Bounds for Successive Projection

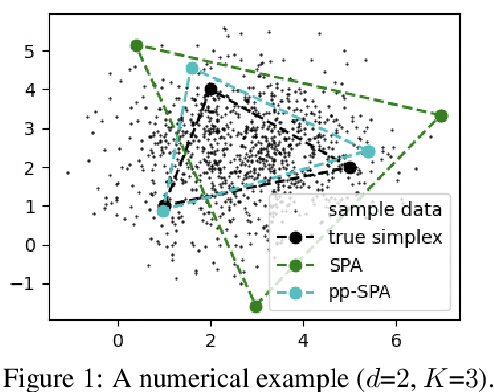
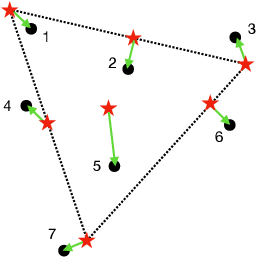
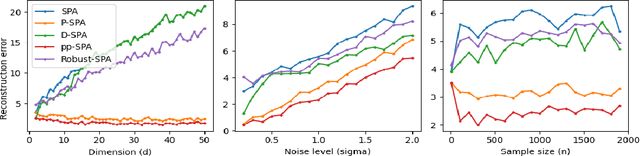
Given a $K$-vertex simplex in a $d$-dimensional space, suppose we measure $n$ points on the simplex with noise (hence, some of the observed points fall outside the simplex). Vertex hunting is the problem of estimating the $K$ vertices of the simplex. A popular vertex hunting algorithm is successive projection algorithm (SPA). However, SPA is observed to perform unsatisfactorily under strong noise or outliers. We propose pseudo-point SPA (pp-SPA). It uses a projection step and a denoise step to generate pseudo-points and feed them into SPA for vertex hunting. We derive error bounds for pp-SPA, leveraging on extreme value theory of (possibly) high-dimensional random vectors. The results suggest that pp-SPA has faster rates and better numerical performances than SPA. Our analysis includes an improved non-asymptotic bound for the original SPA, which is of independent interest.

Recent Advances in Text Analysis

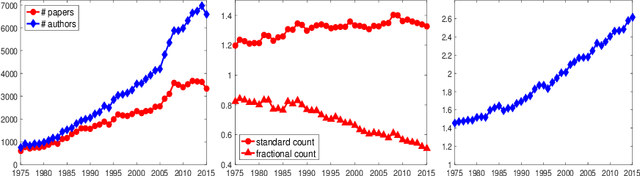
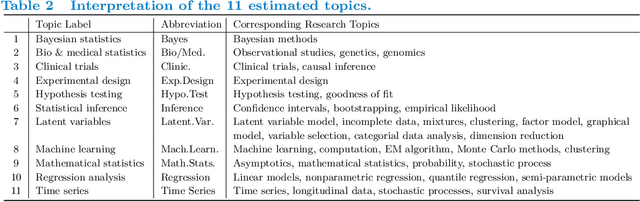
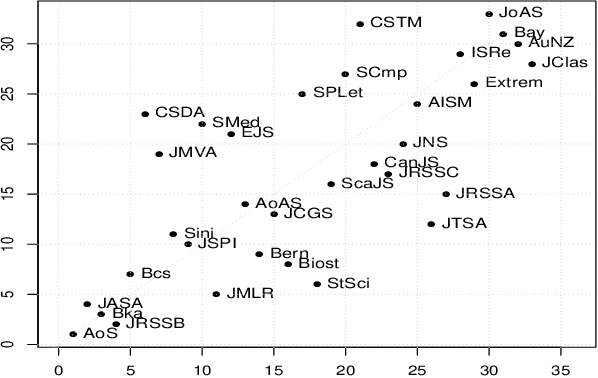
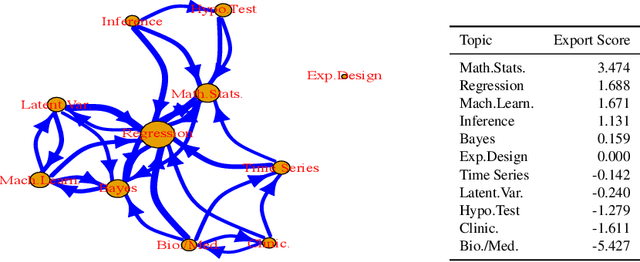
Text analysis is an interesting research area in data science and has various applications, such as in artificial intelligence, biomedical research, and engineering. We review popular methods for text analysis, ranging from topic modeling to the recent neural language models. In particular, we review Topic-SCORE, a statistical approach to topic modeling, and discuss how to use it to analyze MADStat - a dataset on statistical publications that we collected and cleaned. The application of Topic-SCORE and other methods on MADStat leads to interesting findings. For example, $11$ representative topics in statistics are identified. For each journal, the evolution of topic weights over time can be visualized, and these results are used to analyze the trends in statistical research. In particular, we propose a new statistical model for ranking the citation impacts of $11$ topics, and we also build a cross-topic citation graph to illustrate how research results on different topics spread to one another. The results on MADStat provide a data-driven picture of the statistical research in $1975$--$2015$, from a text analysis perspective.

Subject clustering by IF-PCA and several recent methods

Subject clustering (i.e., the use of measured features to cluster subjects, such as patients or cells, into multiple groups) is a problem of great interest. In recent years, many approaches were proposed, among which unsupervised deep learning (UDL) has received a great deal of attention. Two interesting questions are (a) how to combine the strengths of UDL and other approaches, and (b) how these approaches compare to one other. We combine Variational Auto-Encoder (VAE), a popular UDL approach, with the recent idea of Influential Feature PCA (IF-PCA), and propose IF-VAE as a new method for subject clustering. We study IF-VAE and compare it with several other methods (including IF-PCA, VAE, Seurat, and SC3) on $10$ gene microarray data sets and $8$ single-cell RNA-seq data sets. We find that IF-VAE significantly improves over VAE, but still underperforms IF-PCA. We also find that IF-PCA is quite competitive, which slightly outperforms Seurat and SC3 over the $8$ single-cell data sets. IF-PCA is conceptually simple and permits delicate analysis. We demonstrate that IF-PCA is capable of achieving the phase transition in a Rare/Weak model. Comparatively, Seurat and SC3 are more complex and theoretically difficult to analyze (for these reasons, their optimality remains unclear).

Phase transition for detecting a small community in a large network

How to detect a small community in a large network is an interesting problem, including clique detection as a special case, where a naive degree-based $\chi^2$-test was shown to be powerful in the presence of an Erd\H{o}s-Renyi background. Using Sinkhorn's theorem, we show that the signal captured by the $\chi^2$-test may be a modeling artifact, and it may disappear once we replace the Erd\H{o}s-Renyi model by a broader network model. We show that the recent SgnQ test is more appropriate for such a setting. The test is optimal in detecting communities with sizes comparable to the whole network, but has never been studied for our setting, which is substantially different and more challenging. Using a degree-corrected block model (DCBM), we establish phase transitions of this testing problem concerning the size of the small community and the edge densities in small and large communities. When the size of the small community is larger than $\sqrt{n}$, the SgnQ test is optimal for it attains the computational lower bound (CLB), the information lower bound for methods allowing polynomial computation time. When the size of the small community is smaller than $\sqrt{n}$, we establish the parameter regime where the SgnQ test has full power and make some conjectures of the CLB. We also study the classical information lower bound (LB) and show that there is always a gap between the CLB and LB in our range of interest.

Testing High-dimensional Multinomials with Applications to Text Analysis

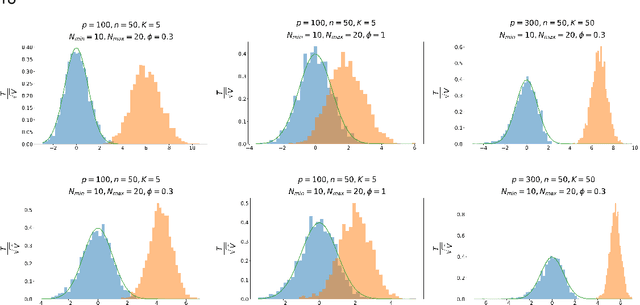
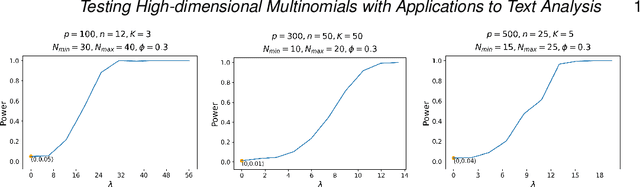
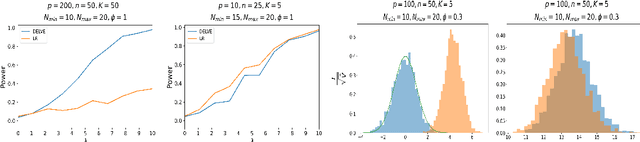
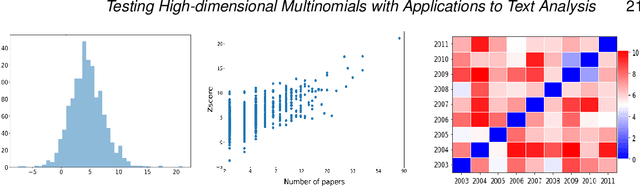
Motivated by applications in text mining and discrete distribution inference, we investigate the testing for equality of probability mass functions of $K$ groups of high-dimensional multinomial distributions. A test statistic, which is shown to have an asymptotic standard normal distribution under the null, is proposed. The optimal detection boundary is established, and the proposed test is shown to achieve this optimal detection boundary across the entire parameter space of interest. The proposed method is demonstrated in simulation studies and applied to analyze two real-world datasets to examine variation among consumer reviews of Amazon movies and diversity of statistical paper abstracts.

Measurement error models: from nonparametric methods to deep neural networks

The success of deep learning has inspired recent interests in applying neural networks in statistical inference. In this paper, we investigate the use of deep neural networks for nonparametric regression with measurement errors. We propose an efficient neural network design for estimating measurement error models, in which we use a fully connected feed-forward neural network (FNN) to approximate the regression function $f(x)$, a normalizing flow to approximate the prior distribution of $X$, and an inference network to approximate the posterior distribution of $X$. Our method utilizes recent advances in variational inference for deep neural networks, such as the importance weight autoencoder, doubly reparametrized gradient estimator, and non-linear independent components estimation. We conduct an extensive numerical study to compare the neural network approach with classical nonparametric methods and observe that the neural network approach is more flexible in accommodating different classes of regression functions and performs superior or comparable to the best available method in nearly all settings.

SCORE+ for Network Community Detection

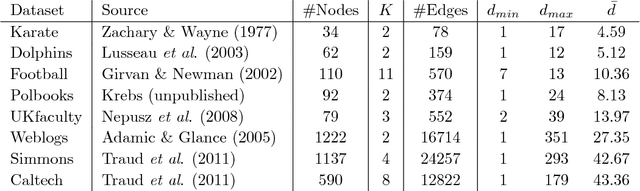
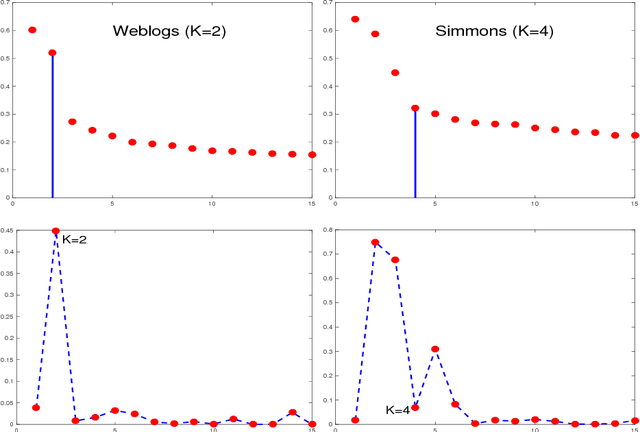
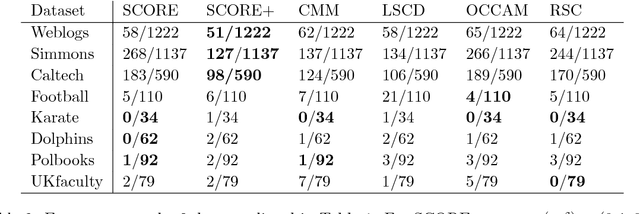
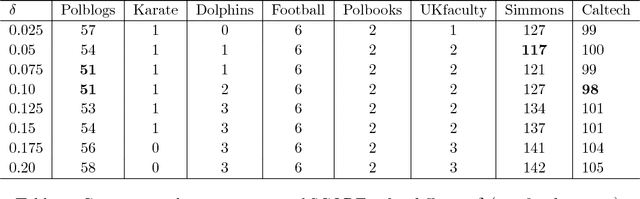
SCORE is a recent approach to network community detection proposed by Jin (2015). In this note, we propose a simple improvement of SCORE, called SCORE+, and compare its performance with several other methods, using 10 different network data sets. For 7 of these data sets, the performances of SCORE and SCORE+ are similar, but for the other 3 data sets (Polbooks, Simmons, Caltech), SCORE+ provides a significant improvement.

State Aggregation Learning from Markov Transition Data

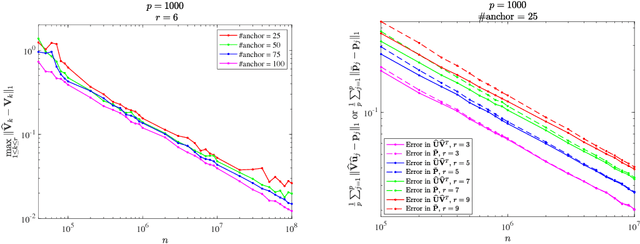
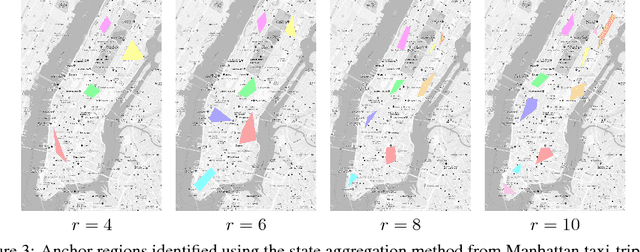
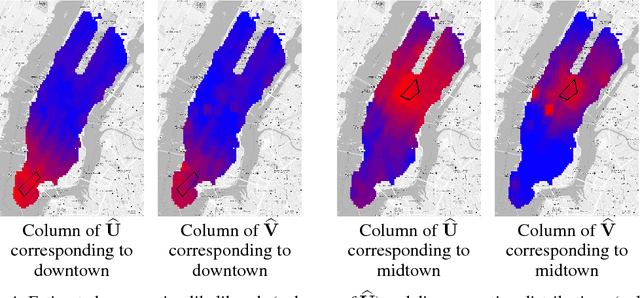
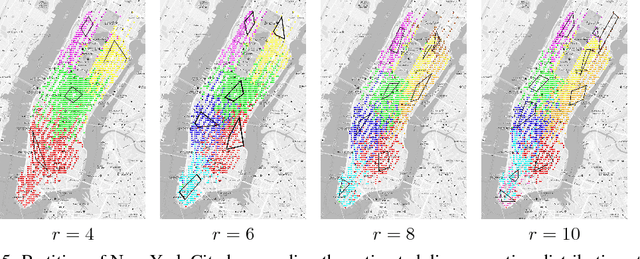
State aggregation is a model reduction method rooted in control theory and reinforcement learning. It reduces the complexity of engineering systems by mapping the system's states into a small number of meta-states. In this paper, we study the unsupervised estimation of unknown state aggregation structures based on Markov trajectories. We formulate the state aggregation of Markov processes into a nonnegative factorization model, where left and right factor matrices correspond to aggregation and disaggregation distributions respectively. By leveraging techniques developed in the context of topic modeling, we propose an efficient polynomial-time algorithm for computing the estimated state aggregation model. Under some "anchor state" assumption, we show that one can reliably recover the state aggregation structure from sample transitions with high probability. Sharp divergence error bounds are proved for the estimated aggregation and disaggregation distributions, and experiments with Manhattan traffic data are provided.

A Geometrical Approach to Topic Model Estimation

In the probabilistic topic models, the quantity of interest---a low-rank matrix consisting of topic vectors---is hidden in the text corpus matrix, masked by noise, and the Singular Value Decomposition (SVD) is a potentially useful tool for learning such a low-rank matrix. However, the connection between this low-rank matrix and the singular vectors of the text corpus matrix are usually complicated and hard to spell out, so how to use SVD for learning topic models faces challenges. In this paper, we overcome the challenge by revealing a surprising insight: there is a low-dimensional simplex structure which can be viewed as a bridge between the low-rank matrix of interest and the SVD of the text corpus matrix, and allows us to conveniently reconstruct the former using the latter. Such an insight motivates a new SVD approach to learning topic models, which we analyze with delicate random matrix theory and derive the rate of convergence. We support our methods and theory numerically, using both simulated data and real data.