Taming "data-hungry" reinforcement learning? Stability in continuous state-action spaces

We introduce a novel framework for analyzing reinforcement learning (RL) in continuous state-action spaces, and use it to prove fast rates of convergence in both off-line and on-line settings. Our analysis highlights two key stability properties, relating to how changes in value functions and/or policies affect the Bellman operator and occupation measures. We argue that these properties are satisfied in many continuous state-action Markov decision processes, and demonstrate how they arise naturally when using linear function approximation methods. Our analysis offers fresh perspectives on the roles of pessimism and optimism in off-line and on-line RL, and highlights the connection between off-line RL and transfer learning.

Policy evaluation from a single path: Multi-step methods, mixing and mis-specification

We study non-parametric estimation of the value function of an infinite-horizon $\gamma$-discounted Markov reward process (MRP) using observations from a single trajectory. We provide non-asymptotic guarantees for a general family of kernel-based multi-step temporal difference (TD) estimates, including canonical $K$-step look-ahead TD for $K = 1, 2, \ldots$ and the TD$(\lambda)$ family for $\lambda \in [0,1)$ as special cases. Our bounds capture its dependence on Bellman fluctuations, mixing time of the Markov chain, any mis-specification in the model, as well as the choice of weight function defining the estimator itself, and reveal some delicate interactions between mixing time and model mis-specification. For a given TD method applied to a well-specified model, its statistical error under trajectory data is similar to that of i.i.d. sample transition pairs, whereas under mis-specification, temporal dependence in data inflates the statistical error. However, any such deterioration can be mitigated by increased look-ahead. We complement our upper bounds by proving minimax lower bounds that establish optimality of TD-based methods with appropriately chosen look-ahead and weighting, and reveal some fundamental differences between value function estimation and ordinary non-parametric regression.

Near-optimal Offline Reinforcement Learning with Linear Representation: Leveraging Variance Information with Pessimism

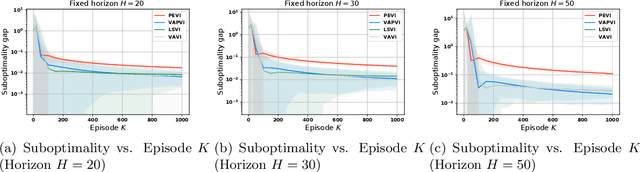
Offline reinforcement learning, which seeks to utilize offline/historical data to optimize sequential decision-making strategies, has gained surging prominence in recent studies. Due to the advantage that appropriate function approximators can help mitigate the sample complexity burden in modern reinforcement learning problems, existing endeavors usually enforce powerful function representation models (e.g. neural networks) to learn the optimal policies. However, a precise understanding of the statistical limits with function representations, remains elusive, even when such a representation is linear. Towards this goal, we study the statistical limits of offline reinforcement learning with linear model representations. To derive the tight offline learning bound, we design the variance-aware pessimistic value iteration (VAPVI), which adopts the conditional variance information of the value function for time-inhomogeneous episodic linear Markov decision processes (MDPs). VAPVI leverages estimated variances of the value functions to reweight the Bellman residuals in the least-square pessimistic value iteration and provides improved offline learning bounds over the best-known existing results (whereas the Bellman residuals are equally weighted by design). More importantly, our learning bounds are expressed in terms of system quantities, which provide natural instance-dependent characterizations that previous results are short of. We hope our results draw a clearer picture of what offline learning should look like when linear representations are provided.

Adaptive and Robust Multi-task Learning

We study the multi-task learning problem that aims to simultaneously analyze multiple datasets collected from different sources and learn one model for each of them. We propose a family of adaptive methods that automatically utilize possible similarities among those tasks while carefully handling their differences. We derive sharp statistical guarantees for the methods and prove their robustness against outlier tasks. Numerical experiments on synthetic and real datasets demonstrate the efficacy of our new methods.

Optimal policy evaluation using kernel-based temporal difference methods

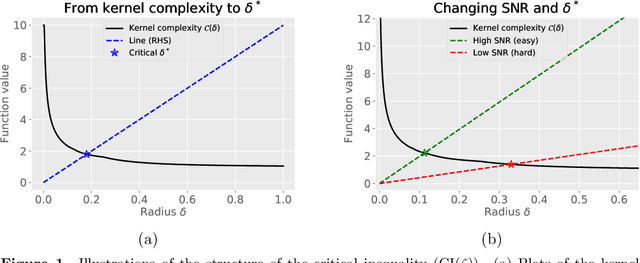
We study methods based on reproducing kernel Hilbert spaces for estimating the value function of an infinite-horizon discounted Markov reward process (MRP). We study a regularized form of the kernel least-squares temporal difference (LSTD) estimate; in the population limit of infinite data, it corresponds to the fixed point of a projected Bellman operator defined by the associated reproducing kernel Hilbert space. The estimator itself is obtained by computing the projected fixed point induced by a regularized version of the empirical operator; due to the underlying kernel structure, this reduces to solving a linear system involving kernel matrices. We analyze the error of this estimate in the $L^2(\mu)$-norm, where $\mu$ denotes the stationary distribution of the underlying Markov chain. Our analysis imposes no assumptions on the transition operator of the Markov chain, but rather only conditions on the reward function and population-level kernel LSTD solutions. We use empirical process theory techniques to derive a non-asymptotic upper bound on the error with explicit dependence on the eigenvalues of the associated kernel operator, as well as the instance-dependent variance of the Bellman residual error. In addition, we prove minimax lower bounds over sub-classes of MRPs, which shows that our rate is optimal in terms of the sample size $n$ and the effective horizon $H = (1 - \gamma)^{-1}$. Whereas existing worst-case theory predicts cubic scaling ($H^3$) in the effective horizon, our theory reveals that there is in fact a much wider range of scalings, depending on the kernel, the stationary distribution, and the variance of the Bellman residual error. Notably, it is only parametric and near-parametric problems that can ever achieve the worst-case cubic scaling.

PU-Flow: a Point Cloud Upsampling Networkwith Normalizing Flows

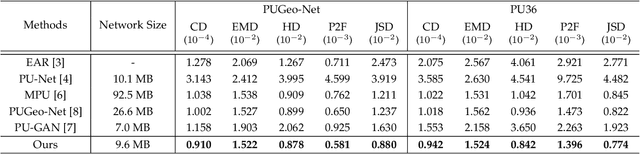
Point cloud upsampling aims to generate dense point clouds from given sparse ones, which is a challenging task due to the irregular and unordered nature of point sets. To address this issue, we present a novel deep learning-based model, called PU-Flow,which incorporates normalizing flows and feature interpolation techniques to produce dense points uniformly distributed on the underlying surface. Specifically, we formulate the upsampling process as point interpolation in a latent space, where the interpolation weights are adaptively learned from local geometric context, and exploit the invertible characteristics of normalizing flows to transform points between Euclidean and latent spaces. We evaluate PU-Flow on a wide range of 3D models with sharp features and high-frequency details. Qualitative and quantitative results show that our method outperforms state-of-the-art deep learning-based approaches in terms of reconstruction quality, proximity-to-surface accuracy, and computation efficiency.

Learning Good State and Action Representations via Tensor Decomposition

The transition kernel of a continuous-state-action Markov decision process (MDP) admits a natural tensor structure. This paper proposes a tensor-inspired unsupervised learning method to identify meaningful low-dimensional state and action representations from empirical trajectories. The method exploits the MDP's tensor structure by kernelization, importance sampling and low-Tucker-rank approximation. This method can be further used to cluster states and actions respectively and find the best discrete MDP abstraction. We provide sharp statistical error bounds for tensor concentration and the preservation of diffusion distance after embedding.

Risk Bounds and Rademacher Complexity in Batch Reinforcement Learning

This paper considers batch Reinforcement Learning (RL) with general value function approximation. Our study investigates the minimal assumptions to reliably estimate/minimize Bellman error, and characterizes the generalization performance by (local) Rademacher complexities of general function classes, which makes initial steps in bridging the gap between statistical learning theory and batch RL. Concretely, we view the Bellman error as a surrogate loss for the optimality gap, and prove the followings: (1) In double sampling regime, the excess risk of Empirical Risk Minimizer (ERM) is bounded by the Rademacher complexity of the function class. (2) In the single sampling regime, sample-efficient risk minimization is not possible without further assumptions, regardless of algorithms. However, with completeness assumptions, the excess risk of FQI and a minimax style algorithm can be again bounded by the Rademacher complexity of the corresponding function classes. (3) Fast statistical rates can be achieved by using tools of local Rademacher complexity. Our analysis covers a wide range of function classes, including finite classes, linear spaces, kernel spaces, sparse linear features, etc.

Bootstrapping Statistical Inference for Off-Policy Evaluation

Bootstrapping provides a flexible and effective approach for assessing the quality of batch reinforcement learning, yet its theoretical property is less understood. In this paper, we study the use of bootstrapping in off-policy evaluation (OPE), and in particular, we focus on the fitted Q-evaluation (FQE) that is known to be minimax-optimal in the tabular and linear-model cases. We propose a bootstrapping FQE method for inferring the distribution of the policy evaluation error and show that this method is asymptotically efficient and distributionally consistent for off-policy statistical inference. To overcome the computation limit of bootstrapping, we further adapt a subsampling procedure that improves the runtime by an order of magnitude. We numerically evaluate the bootrapping method in classical RL environments for confidence interval estimation, estimating the variance of off-policy evaluator, and estimating the correlation between multiple off-policy evaluators.

Sparse Feature Selection Makes Batch Reinforcement Learning More Sample Efficient

This paper provides a statistical analysis of high-dimensional batch Reinforcement Learning (RL) using sparse linear function approximation. When there is a large number of candidate features, our result sheds light on the fact that sparsity-aware methods can make batch RL more sample efficient. We first consider the off-policy policy evaluation problem. To evaluate a new target policy, we analyze a Lasso fitted Q-evaluation method and establish a finite-sample error bound that has no polynomial dependence on the ambient dimension. To reduce the Lasso bias, we further propose a post model-selection estimator that applies fitted Q-evaluation to the features selected via group Lasso. Under an additional signal strength assumption, we derive a sharper instance-dependent error bound that depends on a divergence function measuring the distribution mismatch between the data distribution and occupancy measure of the target policy. Further, we study the Lasso fitted Q-iteration for batch policy optimization and establish a finite-sample error bound depending on the ratio between the number of relevant features and restricted minimal eigenvalue of the data's covariance. In the end, we complement the results with minimax lower bounds for batch-data policy evaluation/optimization that nearly match our upper bounds. The results suggest that having well-conditioned data is crucial for sparse batch policy learning.