Near-optimal Offline Reinforcement Learning with Linear Representation: Leveraging Variance Information with Pessimism
Paper and Code
Mar 11, 2022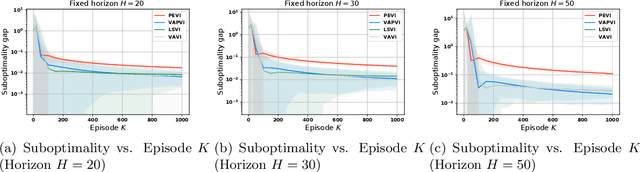
Offline reinforcement learning, which seeks to utilize offline/historical data to optimize sequential decision-making strategies, has gained surging prominence in recent studies. Due to the advantage that appropriate function approximators can help mitigate the sample complexity burden in modern reinforcement learning problems, existing endeavors usually enforce powerful function representation models (e.g. neural networks) to learn the optimal policies. However, a precise understanding of the statistical limits with function representations, remains elusive, even when such a representation is linear. Towards this goal, we study the statistical limits of offline reinforcement learning with linear model representations. To derive the tight offline learning bound, we design the variance-aware pessimistic value iteration (VAPVI), which adopts the conditional variance information of the value function for time-inhomogeneous episodic linear Markov decision processes (MDPs). VAPVI leverages estimated variances of the value functions to reweight the Bellman residuals in the least-square pessimistic value iteration and provides improved offline learning bounds over the best-known existing results (whereas the Bellman residuals are equally weighted by design). More importantly, our learning bounds are expressed in terms of system quantities, which provide natural instance-dependent characterizations that previous results are short of. We hope our results draw a clearer picture of what offline learning should look like when linear representations are provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge