Chengzhuo Ni
Diffusion Model for Data-Driven Black-Box Optimization
Mar 20, 2024



Abstract:Generative AI has redefined artificial intelligence, enabling the creation of innovative content and customized solutions that drive business practices into a new era of efficiency and creativity. In this paper, we focus on diffusion models, a powerful generative AI technology, and investigate their potential for black-box optimization over complex structured variables. Consider the practical scenario where one wants to optimize some structured design in a high-dimensional space, based on massive unlabeled data (representing design variables) and a small labeled dataset. We study two practical types of labels: 1) noisy measurements of a real-valued reward function and 2) human preference based on pairwise comparisons. The goal is to generate new designs that are near-optimal and preserve the designed latent structures. Our proposed method reformulates the design optimization problem into a conditional sampling problem, which allows us to leverage the power of diffusion models for modeling complex distributions. In particular, we propose a reward-directed conditional diffusion model, to be trained on the mixed data, for sampling a near-optimal solution conditioned on high predicted rewards. Theoretically, we establish sub-optimality error bounds for the generated designs. The sub-optimality gap nearly matches the optimal guarantee in off-policy bandits, demonstrating the efficiency of reward-directed diffusion models for black-box optimization. Moreover, when the data admits a low-dimensional latent subspace structure, our model efficiently generates high-fidelity designs that closely respect the latent structure. We provide empirical experiments validating our model in decision-making and content-creation tasks.
Reward-Directed Conditional Diffusion: Provable Distribution Estimation and Reward Improvement
Jul 13, 2023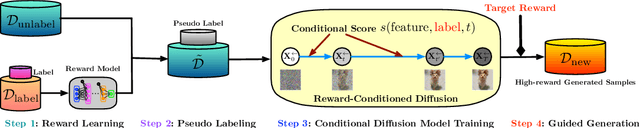
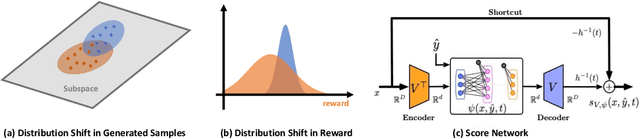
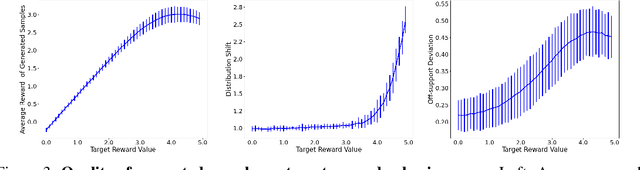
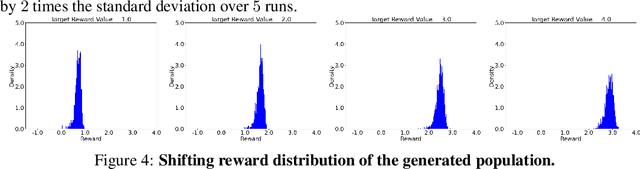
Abstract:We explore the methodology and theory of reward-directed generation via conditional diffusion models. Directed generation aims to generate samples with desired properties as measured by a reward function, which has broad applications in generative AI, reinforcement learning, and computational biology. We consider the common learning scenario where the data set consists of unlabeled data along with a smaller set of data with noisy reward labels. Our approach leverages a learned reward function on the smaller data set as a pseudolabeler. From a theoretical standpoint, we show that this directed generator can effectively learn and sample from the reward-conditioned data distribution. Additionally, our model is capable of recovering the latent subspace representation of data. Moreover, we establish that the model generates a new population that moves closer to a user-specified target reward value, where the optimality gap aligns with the off-policy bandit regret in the feature subspace. The improvement in rewards obtained is influenced by the interplay between the strength of the reward signal, the distribution shift, and the cost of off-support extrapolation. We provide empirical results to validate our theory and highlight the relationship between the strength of extrapolation and the quality of generated samples.
Representation Learning for General-sum Low-rank Markov Games
Oct 30, 2022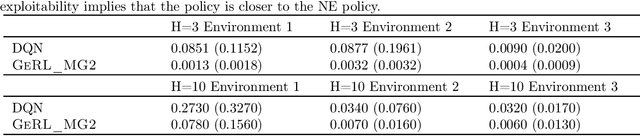
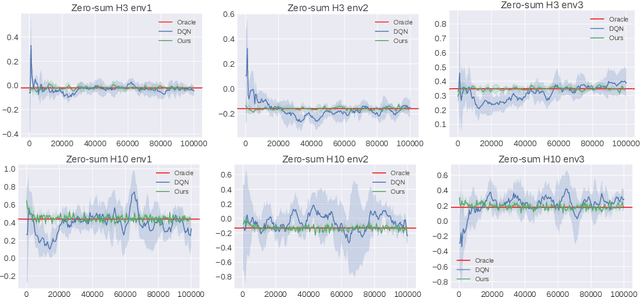
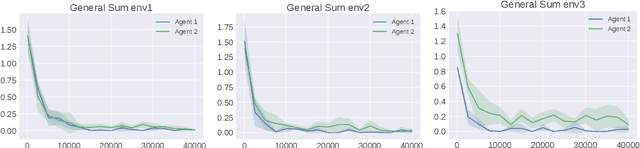

Abstract:We study multi-agent general-sum Markov games with nonlinear function approximation. We focus on low-rank Markov games whose transition matrix admits a hidden low-rank structure on top of an unknown non-linear representation. The goal is to design an algorithm that (1) finds an $\varepsilon$-equilibrium policy sample efficiently without prior knowledge of the environment or the representation, and (2) permits a deep-learning friendly implementation. We leverage representation learning and present a model-based and a model-free approach to construct an effective representation from the collected data. For both approaches, the algorithm achieves a sample complexity of poly$(H,d,A,1/\varepsilon)$, where $H$ is the game horizon, $d$ is the dimension of the feature vector, $A$ is the size of the joint action space and $\varepsilon$ is the optimality gap. When the number of players is large, the above sample complexity can scale exponentially with the number of players in the worst case. To address this challenge, we consider Markov games with a factorized transition structure and present an algorithm that escapes such exponential scaling. To our best knowledge, this is the first sample-efficient algorithm for multi-agent general-sum Markov games that incorporates (non-linear) function approximation. We accompany our theoretical result with a neural network-based implementation of our algorithm and evaluate it against the widely used deep RL baseline, DQN with fictitious play.
Bandit Theory and Thompson Sampling-Guided Directed Evolution for Sequence Optimization
Jun 05, 2022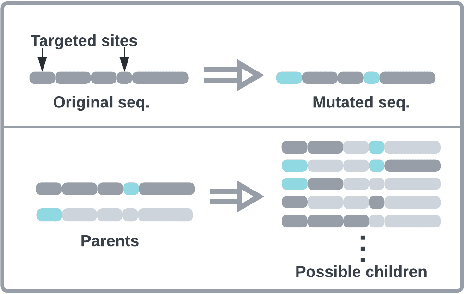
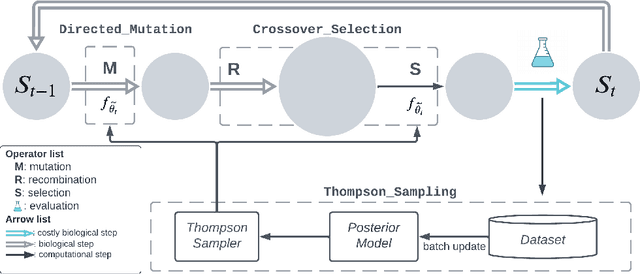
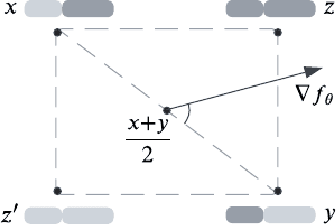
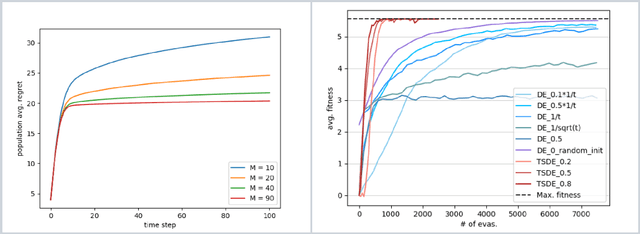
Abstract:Directed Evolution (DE), a landmark wet-lab method originated in 1960s, enables discovery of novel protein designs via evolving a population of candidate sequences. Recent advances in biotechnology has made it possible to collect high-throughput data, allowing the use of machine learning to map out a protein's sequence-to-function relation. There is a growing interest in machine learning-assisted DE for accelerating protein optimization. Yet the theoretical understanding of DE, as well as the use of machine learning in DE, remains limited. In this paper, we connect DE with the bandit learning theory and make a first attempt to study regret minimization in DE. We propose a Thompson Sampling-guided Directed Evolution (TS-DE) framework for sequence optimization, where the sequence-to-function mapping is unknown and querying a single value is subject to costly and noisy measurements. TS-DE updates a posterior of the function based on collected measurements. It uses a posterior-sampled function estimate to guide the crossover recombination and mutation steps in DE. In the case of a linear model, we show that TS-DE enjoys a Bayesian regret of order $\tilde O(d^{2}\sqrt{MT})$, where $d$ is feature dimension, $M$ is population size and $T$ is number of rounds. This regret bound is nearly optimal, confirming that bandit learning can provably accelerate DE. It may have implications for more general sequence optimization and evolutionary algorithms.
Off-Policy Fitted Q-Evaluation with Differentiable Function Approximators: Z-Estimation and Inference Theory
Feb 10, 2022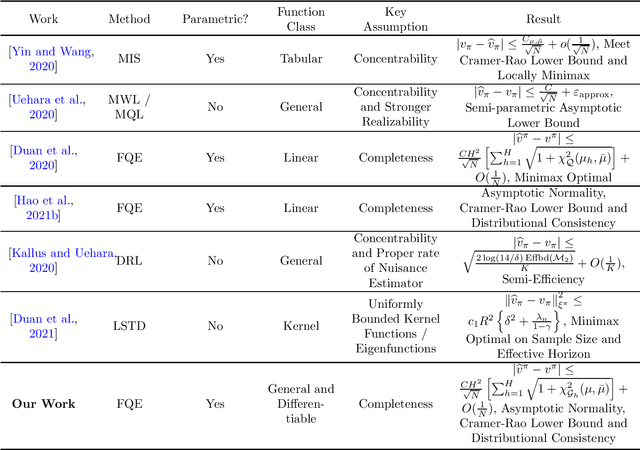
Abstract:Off-Policy Evaluation (OPE) serves as one of the cornerstones in Reinforcement Learning (RL). Fitted Q Evaluation (FQE) with various function approximators, especially deep neural networks, has gained practical success. While statistical analysis has proved FQE to be minimax-optimal with tabular, linear and several nonparametric function families, its practical performance with more general function approximator is less theoretically understood. We focus on FQE with general differentiable function approximators, making our theory applicable to neural function approximations. We approach this problem using the Z-estimation theory and establish the following results: The FQE estimation error is asymptotically normal with explicit variance determined jointly by the tangent space of the function class at the ground truth, the reward structure, and the distribution shift due to off-policy learning; The finite-sample FQE error bound is dominated by the same variance term, and it can also be bounded by function class-dependent divergence, which measures how the off-policy distribution shift intertwines with the function approximator. In addition, we study bootstrapping FQE estimators for error distribution inference and estimating confidence intervals, accompanied by a Cramer-Rao lower bound that matches our upper bounds. The Z-estimation analysis provides a generalizable theoretical framework for studying off-policy estimation in RL and provides sharp statistical theory for FQE with differentiable function approximators.
Optimal Estimation of Off-Policy Policy Gradient via Double Fitted Iteration
Jan 31, 2022
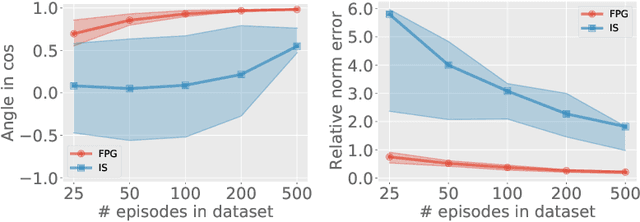
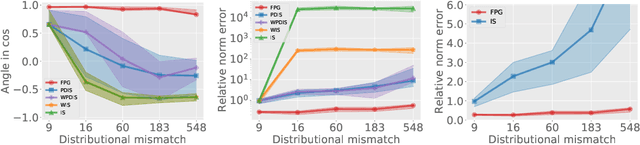
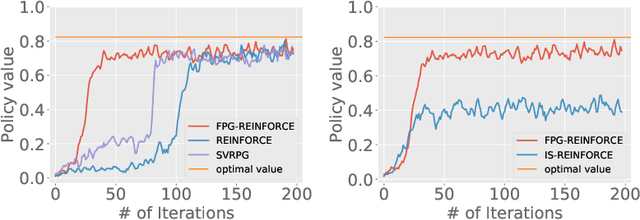
Abstract:Policy gradient (PG) estimation becomes a challenge when we are not allowed to sample with the target policy but only have access to a dataset generated by some unknown behavior policy. Conventional methods for off-policy PG estimation often suffer from either significant bias or exponentially large variance. In this paper, we propose the double Fitted PG estimation (FPG) algorithm. FPG can work with an arbitrary policy parameterization, assuming access to a Bellman-complete value function class. In the case of linear value function approximation, we provide a tight finite-sample upper bound on policy gradient estimation error, that is governed by the amount of distribution mismatch measured in feature space. We also establish the asymptotic normality of FPG estimation error with a precise covariance characterization, which is further shown to be statistically optimal with a matching Cramer-Rao lower bound. Empirically, we evaluate the performance of FPG on both policy gradient estimation and policy optimization, using either softmax tabular or ReLU policy networks. Under various metrics, our results show that FPG significantly outperforms existing off-policy PG estimation methods based on importance sampling and variance reduction techniques.
Learning Good State and Action Representations via Tensor Decomposition
May 03, 2021



Abstract:The transition kernel of a continuous-state-action Markov decision process (MDP) admits a natural tensor structure. This paper proposes a tensor-inspired unsupervised learning method to identify meaningful low-dimensional state and action representations from empirical trajectories. The method exploits the MDP's tensor structure by kernelization, importance sampling and low-Tucker-rank approximation. This method can be further used to cluster states and actions respectively and find the best discrete MDP abstraction. We provide sharp statistical error bounds for tensor concentration and the preservation of diffusion distance after embedding.
On the Convergence and Sample Efficiency of Variance-Reduced Policy Gradient Method
Feb 17, 2021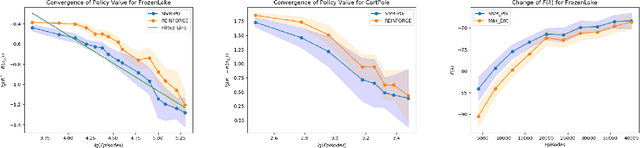
Abstract:Policy gradient gives rise to a rich class of reinforcement learning (RL) methods, for example the REINFORCE. Yet the best known sample complexity result for such methods to find an $\epsilon$-optimal policy is $\mathcal{O}(\epsilon^{-3})$, which is suboptimal. In this paper, we study the fundamental convergence properties and sample efficiency of first-order policy optimization method. We focus on a generalized variant of policy gradient method, which is able to maximize not only a cumulative sum of rewards but also a general utility function over a policy's long-term visiting distribution. By exploiting the problem's hidden convex nature and leveraging techniques from composition optimization, we propose a Stochastic Incremental Variance-Reduced Policy Gradient (SIVR-PG) approach that improves a sequence of policies to provably converge to the global optimal solution and finds an $\epsilon$-optimal policy using $\tilde{\mathcal{O}}(\epsilon^{-2})$ samples.
Learning to Control in Metric Space with Optimal Regret
May 05, 2019Abstract:We study online reinforcement learning for finite-horizon deterministic control systems with {\it arbitrary} state and action spaces. Suppose that the transition dynamics and reward function is unknown, but the state and action space is endowed with a metric that characterizes the proximity between different states and actions. We provide a surprisingly simple upper-confidence reinforcement learning algorithm that uses a function approximation oracle to estimate optimistic Q functions from experiences. We show that the regret of the algorithm after $K$ episodes is $O(HL(KH)^{\frac{d-1}{d}}) $ where $L$ is a smoothness parameter, and $d$ is the doubling dimension of the state-action space with respect to the given metric. We also establish a near-matching regret lower bound. The proposed method can be adapted to work for more structured transition systems, including the finite-state case and the case where value functions are linear combinations of features, where the method also achieve the optimal regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge