Csaba Szepesvári
Eluder dimension: localise it!
Jan 14, 2026Abstract:We establish a lower bound on the eluder dimension of generalised linear model classes, showing that standard eluder dimension-based analysis cannot lead to first-order regret bounds. To address this, we introduce a localisation method for the eluder dimension; our analysis immediately recovers and improves on classic results for Bernoulli bandits, and allows for the first genuine first-order bounds for finite-horizon reinforcement learning tasks with bounded cumulative returns.
Frontier LLMs Still Struggle with Simple Reasoning Tasks
Jul 09, 2025
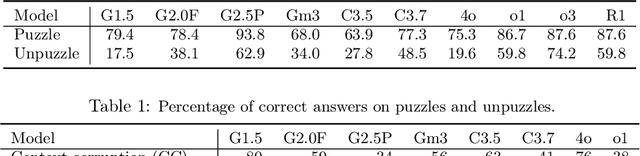
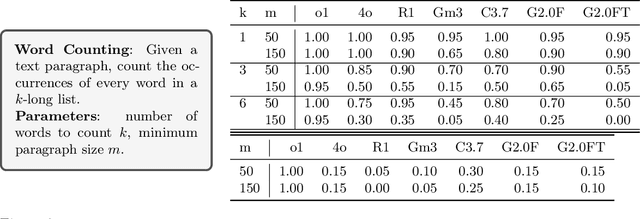
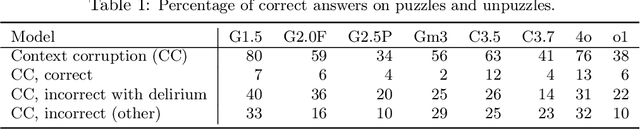
Abstract:While state-of-the-art large language models (LLMs) demonstrate advanced reasoning capabilities-achieving remarkable performance on challenging competitive math and coding benchmarks-they also frequently fail on tasks that are easy for humans. This work studies the performance of frontier LLMs on a broad set of such "easy" reasoning problems. By extending previous work in the literature, we create a suite of procedurally generated simple reasoning tasks, including counting, first-order logic, proof trees, and travel planning, with changeable parameters (such as document length. or the number of variables in a math problem) that can arbitrarily increase the amount of computation required to produce the answer while preserving the fundamental difficulty. While previous work showed that traditional, non-thinking models can be made to fail on such problems, we demonstrate that even state-of-the-art thinking models consistently fail on such problems and for similar reasons (e.g. statistical shortcuts, errors in intermediate steps, and difficulties in processing long contexts). To further understand the behavior of the models, we introduce the unpuzzles dataset, a different "easy" benchmark consisting of trivialized versions of well-known math and logic puzzles. Interestingly, while modern LLMs excel at solving the original puzzles, they tend to fail on the trivialized versions, exhibiting several systematic failure patterns related to memorizing the originals. We show that this happens even if the models are otherwise able to solve problems with different descriptions but requiring the same logic. Our results highlight that out-of-distribution generalization is still problematic for frontier language models and the new generation of thinking models, even for simple reasoning tasks, and making tasks easier does not necessarily imply improved performance.
Almost Free: Self-concordance in Natural Exponential Families and an Application to Bandits
Oct 01, 2024Abstract:We prove that single-parameter natural exponential families with subexponential tails are self-concordant with polynomial-sized parameters. For subgaussian natural exponential families we establish an exact characterization of the growth rate of the self-concordance parameter. Applying these findings to bandits allows us to fill gaps in the literature: We show that optimistic algorithms for generalized linear bandits enjoy regret bounds that are both second-order (scale with the variance of the optimal arm's reward distribution) and free of an exponential dependence on the bound of the problem parameter in the leading term. To the best of our knowledge, ours is the first regret bound for generalized linear bandits with subexponential tails, broadening the class of problems to include Poisson, exponential and gamma bandits.
Confident Natural Policy Gradient for Local Planning in $q_π$-realizable Constrained MDPs
Jun 26, 2024Abstract:The constrained Markov decision process (CMDP) framework emerges as an important reinforcement learning approach for imposing safety or other critical objectives while maximizing cumulative reward. However, the current understanding of how to learn efficiently in a CMDP environment with a potentially infinite number of states remains under investigation, particularly when function approximation is applied to the value functions. In this paper, we address the learning problem given linear function approximation with $q_{\pi}$-realizability, where the value functions of all policies are linearly representable with a known feature map, a setting known to be more general and challenging than other linear settings. Utilizing a local-access model, we propose a novel primal-dual algorithm that, after $\tilde{O}(\text{poly}(d) \epsilon^{-3})$ queries, outputs with high probability a policy that strictly satisfies the constraints while nearly optimizing the value with respect to a reward function. Here, $d$ is the feature dimension and $\epsilon > 0$ is a given error. The algorithm relies on a carefully crafted off-policy evaluation procedure to evaluate the policy using historical data, which informs policy updates through policy gradients and conserves samples. To our knowledge, this is the first result achieving polynomial sample complexity for CMDP in the $q_{\pi}$-realizable setting.
Trajectory Data Suffices for Statistically Efficient Learning in Offline RL with Linear $q^π$-Realizability and Concentrability
May 27, 2024Abstract:We consider offline reinforcement learning (RL) in $H$-horizon Markov decision processes (MDPs) under the linear $q^\pi$-realizability assumption, where the action-value function of every policy is linear with respect to a given $d$-dimensional feature function. The hope in this setting is that learning a good policy will be possible without requiring a sample size that scales with the number of states in the MDP. Foster et al. [2021] have shown this to be impossible even under $\textit{concentrability}$, a data coverage assumption where a coefficient $C_\text{conc}$ bounds the extent to which the state-action distribution of any policy can veer off the data distribution. However, the data in this previous work was in the form of a sequence of individual transitions. This leaves open the question of whether the negative result mentioned could be overcome if the data was composed of sequences of full trajectories. In this work we answer this question positively by proving that with trajectory data, a dataset of size $\text{poly}(d,H,C_\text{conc})/\epsilon^2$ is sufficient for deriving an $\epsilon$-optimal policy, regardless of the size of the state space. The main tool that makes this result possible is due to Weisz et al. [2023], who demonstrate that linear MDPs can be used to approximate linearly $q^\pi$-realizable MDPs. The connection to trajectory data is that the linear MDP approximation relies on "skipping" over certain states. The associated estimation problems are thus easy when working with trajectory data, while they remain nontrivial when working with individual transitions. The question of computational efficiency under our assumptions remains open.
Regret Minimization via Saddle Point Optimization
Mar 15, 2024Abstract:A long line of works characterizes the sample complexity of regret minimization in sequential decision-making by min-max programs. In the corresponding saddle-point game, the min-player optimizes the sampling distribution against an adversarial max-player that chooses confusing models leading to large regret. The most recent instantiation of this idea is the decision-estimation coefficient (DEC), which was shown to provide nearly tight lower and upper bounds on the worst-case expected regret in structured bandits and reinforcement learning. By re-parametrizing the offset DEC with the confidence radius and solving the corresponding min-max program, we derive an anytime variant of the Estimation-To-Decisions (E2D) algorithm. Importantly, the algorithm optimizes the exploration-exploitation trade-off online instead of via the analysis. Our formulation leads to a practical algorithm for finite model classes and linear feedback models. We further point out connections to the information ratio, decoupling coefficient and PAC-DEC, and numerically evaluate the performance of E2D on simple examples.
Switching the Loss Reduces the Cost in Batch Reinforcement Learning
Mar 12, 2024
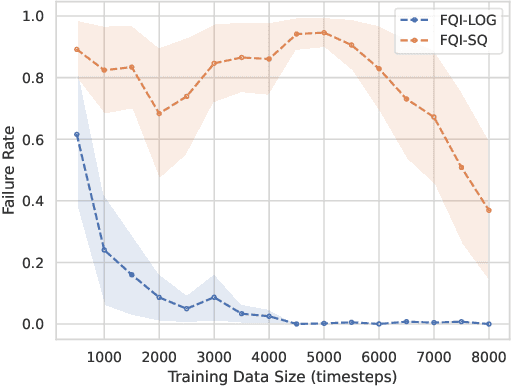
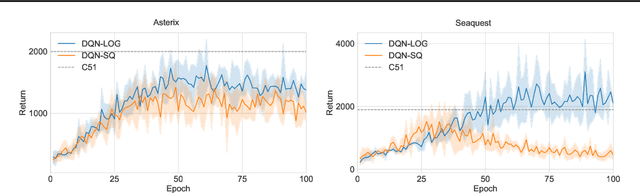
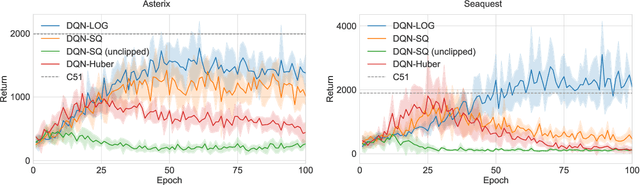
Abstract:We propose training fitted Q-iteration with log-loss (FQI-LOG) for batch reinforcement learning (RL). We show that the number of samples needed to learn a near-optimal policy with FQI-LOG scales with the accumulated cost of the optimal policy, which is zero in problems where acting optimally achieves the goal and incurs no cost. In doing so, we provide a general framework for proving $\textit{small-cost}$ bounds, i.e. bounds that scale with the optimal achievable cost, in batch RL. Moreover, we empirically verify that FQI-LOG uses fewer samples than FQI trained with squared loss on problems where the optimal policy reliably achieves the goal.
Ensemble sampling for linear bandits: small ensembles suffice
Nov 14, 2023Abstract:We provide the first useful, rigorous analysis of ensemble sampling for the stochastic linear bandit setting. In particular, we show that, under standard assumptions, for a $d$-dimensional stochastic linear bandit with an interaction horizon $T$, ensemble sampling with an ensemble of size $m$ on the order of $d \log T$ incurs regret bounded by order $(d \log T)^{5/2} \sqrt{T}$. Ours is the first result in any structured setting not to require the size of the ensemble to scale linearly with $T$ -- which defeats the purpose of ensemble sampling -- while obtaining near $\sqrt{T}$ order regret. Ours is also the first result that allows infinite action sets.
Exploration via linearly perturbed loss minimisation
Nov 13, 2023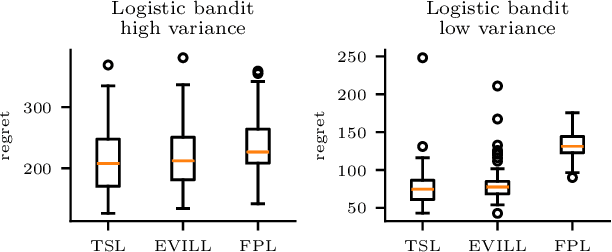
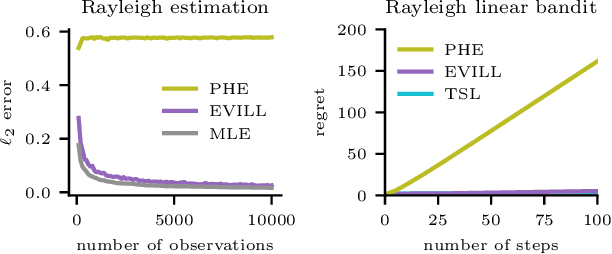
Abstract:We introduce exploration via linear loss perturbations (EVILL), a randomised exploration method for structured stochastic bandit problems that works by solving for the minimiser of a linearly perturbed regularised negative log-likelihood function. We show that, for the case of generalised linear bandits, EVILL reduces to perturbed history exploration (PHE), a method where exploration is done by training on randomly perturbed rewards. In doing so, we provide a simple and clean explanation of when and why random reward perturbations give rise to good bandit algorithms. With the data-dependent perturbations we propose, not present in previous PHE-type methods, EVILL is shown to match the performance of Thompson-sampling-style parameter-perturbation methods, both in theory and in practice. Moreover, we show an example outside of generalised linear bandits where PHE leads to inconsistent estimates, and thus linear regret, while EVILL remains performant. Like PHE, EVILL can be implemented in just a few lines of code.
Stochastic Gradient Descent for Gaussian Processes Done Right
Oct 31, 2023



Abstract:We study the optimisation problem associated with Gaussian process regression using squared loss. The most common approach to this problem is to apply an exact solver, such as conjugate gradient descent, either directly, or to a reduced-order version of the problem. Recently, driven by successes in deep learning, stochastic gradient descent has gained traction as an alternative. In this paper, we show that when done right$\unicode{x2014}$by which we mean using specific insights from the optimisation and kernel communities$\unicode{x2014}$this approach is highly effective. We thus introduce a particular stochastic dual gradient descent algorithm, that may be implemented with a few lines of code using any deep learning framework. We explain our design decisions by illustrating their advantage against alternatives with ablation studies and show that the new method is highly competitive. Our evaluations on standard regression benchmarks and a Bayesian optimisation task set our approach apart from preconditioned conjugate gradients, variational Gaussian process approximations, and a previous version of stochastic gradient descent for Gaussian processes. On a molecular binding affinity prediction task, our method places Gaussian process regression on par in terms of performance with state-of-the-art graph neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge