Confidence Estimation via Sequential Likelihood Mixing

We present a universal framework for constructing confidence sets based on sequential likelihood mixing. Building upon classical results from sequential analysis, we provide a unifying perspective on several recent lines of work, and establish fundamental connections between sequential mixing, Bayesian inference and regret inequalities from online estimation. The framework applies to any realizable family of likelihood functions and allows for non-i.i.d. data and anytime validity. Moreover, the framework seamlessly integrates standard approximate inference techniques, such as variational inference and sampling-based methods, and extends to misspecified model classes, while preserving provable coverage guarantees. We illustrate the power of the framework by deriving tighter confidence sequences for classical settings, including sequential linear regression and sparse estimation, with simplified proofs.

Regret Minimization via Saddle Point Optimization

A long line of works characterizes the sample complexity of regret minimization in sequential decision-making by min-max programs. In the corresponding saddle-point game, the min-player optimizes the sampling distribution against an adversarial max-player that chooses confusing models leading to large regret. The most recent instantiation of this idea is the decision-estimation coefficient (DEC), which was shown to provide nearly tight lower and upper bounds on the worst-case expected regret in structured bandits and reinforcement learning. By re-parametrizing the offset DEC with the confidence radius and solving the corresponding min-max program, we derive an anytime variant of the Estimation-To-Decisions (E2D) algorithm. Importantly, the algorithm optimizes the exploration-exploitation trade-off online instead of via the analysis. Our formulation leads to a practical algorithm for finite model classes and linear feedback models. We further point out connections to the information ratio, decoupling coefficient and PAC-DEC, and numerically evaluate the performance of E2D on simple examples.

Efficient Planning in Combinatorial Action Spaces with Applications to Cooperative Multi-Agent Reinforcement Learning

A practical challenge in reinforcement learning are combinatorial action spaces that make planning computationally demanding. For example, in cooperative multi-agent reinforcement learning, a potentially large number of agents jointly optimize a global reward function, which leads to a combinatorial blow-up in the action space by the number of agents. As a minimal requirement, we assume access to an argmax oracle that allows to efficiently compute the greedy policy for any Q-function in the model class. Building on recent work in planning with local access to a simulator and linear function approximation, we propose efficient algorithms for this setting that lead to polynomial compute and query complexity in all relevant problem parameters. For the special case where the feature decomposition is additive, we further improve the bounds and extend the results to the kernelized setting with an efficient algorithm.

Linear Partial Monitoring for Sequential Decision-Making: Algorithms, Regret Bounds and Applications

Partial monitoring is an expressive framework for sequential decision-making with an abundance of applications, including graph-structured and dueling bandits, dynamic pricing and transductive feedback models. We survey and extend recent results on the linear formulation of partial monitoring that naturally generalizes the standard linear bandit setting. The main result is that a single algorithm, information-directed sampling (IDS), is (nearly) worst-case rate optimal in all finite-action games. We present a simple and unified analysis of stochastic partial monitoring, and further extend the model to the contextual and kernelized setting.

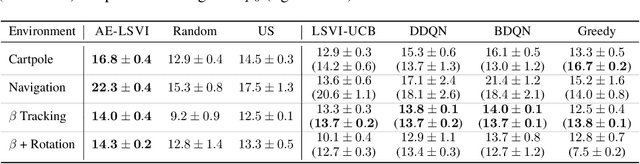
Near-optimal Policy Identification in Active Reinforcement Learning

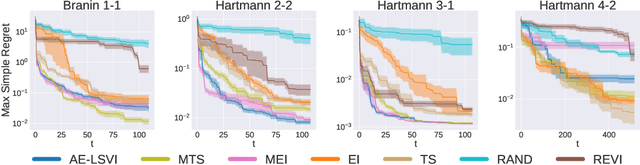
Many real-world reinforcement learning tasks require control of complex dynamical systems that involve both costly data acquisition processes and large state spaces. In cases where the transition dynamics can be readily evaluated at specified states (e.g., via a simulator), agents can operate in what is often referred to as planning with a \emph{generative model}. We propose the AE-LSVI algorithm for best-policy identification, a novel variant of the kernelized least-squares value iteration (LSVI) algorithm that combines optimism with pessimism for active exploration (AE). AE-LSVI provably identifies a near-optimal policy \emph{uniformly} over an entire state space and achieves polynomial sample complexity guarantees that are independent of the number of states. When specialized to the recently introduced offline contextual Bayesian optimization setting, our algorithm achieves improved sample complexity bounds. Experimentally, we demonstrate that AE-LSVI outperforms other RL algorithms in a variety of environments when robustness to the initial state is required.

Managing Temporal Resolution in Continuous Value Estimation: A Fundamental Trade-off

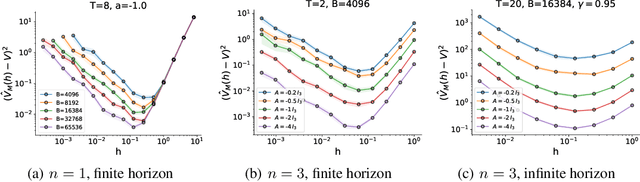
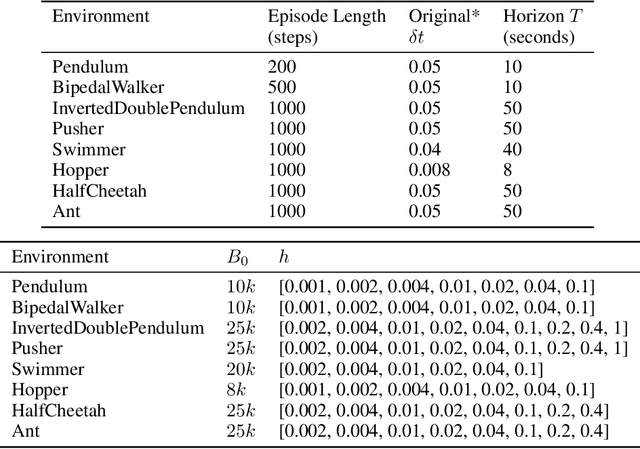
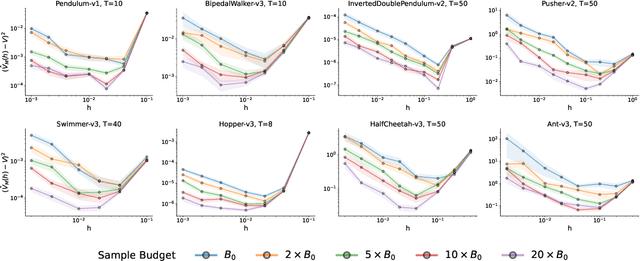
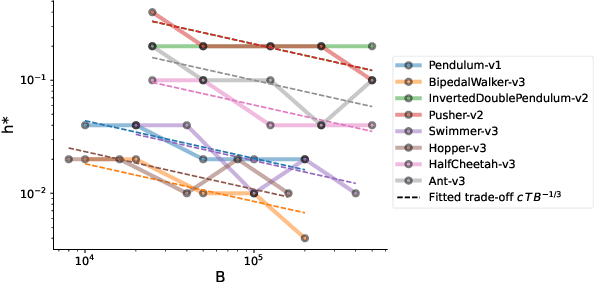
A default assumption in reinforcement learning and optimal control is that experience arrives at discrete time points on a fixed clock cycle. Many applications, however, involve continuous systems where the time discretization is not fixed but instead can be managed by a learning algorithm. By analyzing Monte-Carlo value estimation for LQR systems in both finite-horizon and infinite-horizon settings, we uncover a fundamental trade-off between approximation and statistical error in value estimation. Importantly, these two errors behave differently with respect to time discretization, which implies that there is an optimal choice for the temporal resolution that depends on the data budget. These findings show how adapting the temporal resolution can provably improve value estimation quality in LQR systems from finite data. Empirically, we demonstrate the trade-off in numerical simulations of LQR instances and several non-linear environments.

Tuning Particle Accelerators with Safety Constraints using Bayesian Optimization

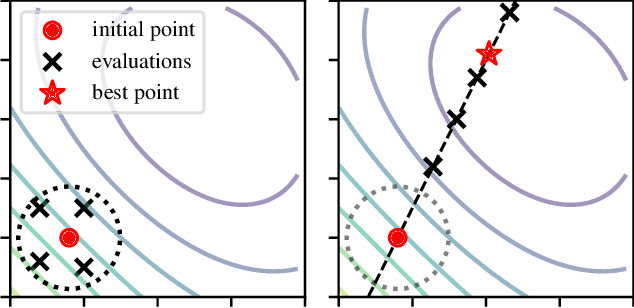
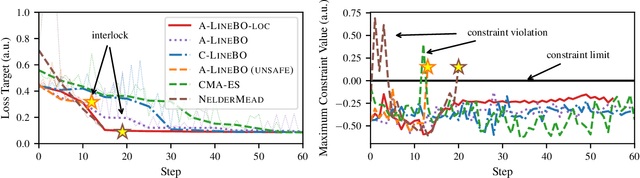
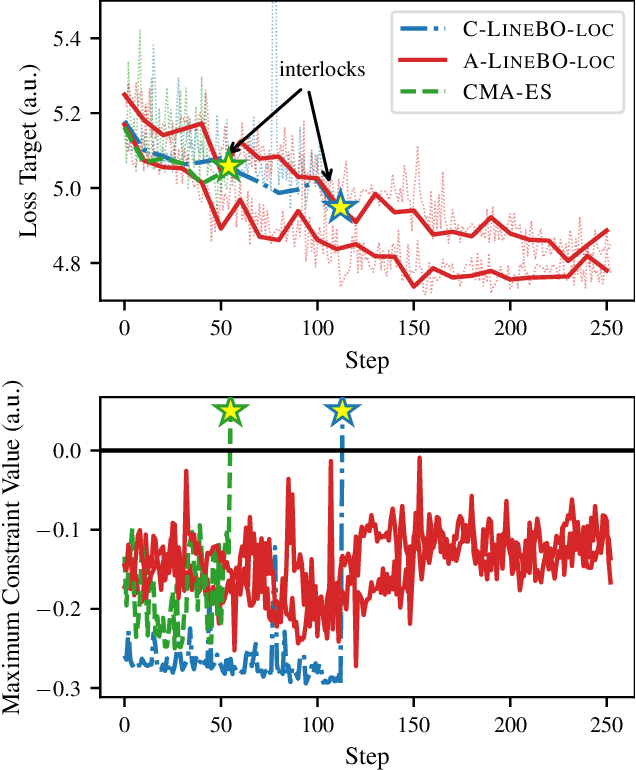
Tuning machine parameters of particle accelerators is a repetitive and time-consuming task, that is challenging to automate. While many off-the-shelf optimization algorithms are available, in practice their use is limited because most methods do not account for safety-critical constraints that apply to each iteration, including loss signals or step-size limitations. One notable exception is safe Bayesian optimization, which is a data-driven tuning approach for global optimization with noisy feedback. We propose and evaluate a step size-limited variant of safe Bayesian optimization on two research faculties of the Paul Scherrer Institut (PSI): a) the Swiss Free Electron Laser (SwissFEL) and b) the High-Intensity Proton Accelerator (HIPA). We report promising experimental results on both machines, tuning up to 16 parameters subject to more than 200 constraints.

Bias-Robust Bayesian Optimization via Dueling Bandits

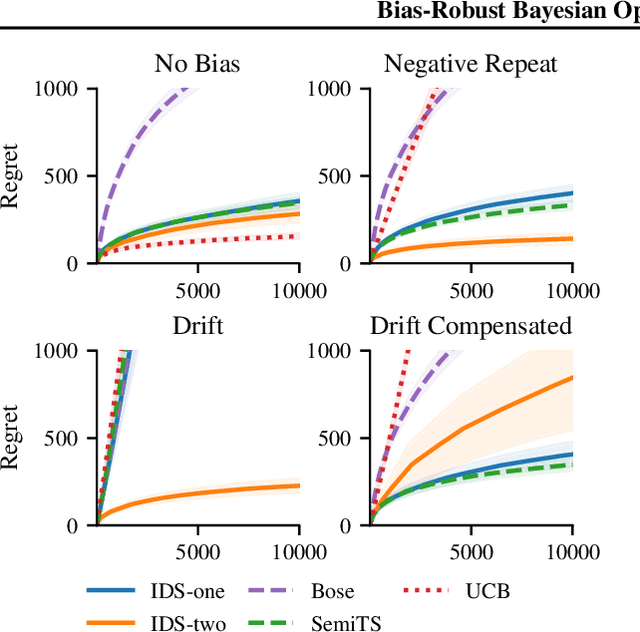
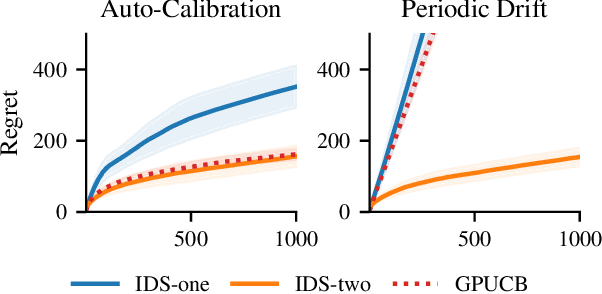
We consider Bayesian optimization in settings where observations can be adversarially biased, for example by an uncontrolled hidden confounder. Our first contribution is a reduction of the confounded setting to the dueling bandit model. Then we propose a novel approach for dueling bandits based on information-directed sampling (IDS). Thereby, we obtain the first efficient kernelized algorithm for dueling bandits that comes with cumulative regret guarantees. Our analysis further generalizes a previously proposed semi-parametric linear bandit model to non-linear reward functions, and uncovers interesting links to doubly-robust estimation.

Efficient Pure Exploration for Combinatorial Bandits with Semi-Bandit Feedback

Combinatorial bandits with semi-bandit feedback generalize multi-armed bandits, where the agent chooses sets of arms and observes a noisy reward for each arm contained in the chosen set. The action set satisfies a given structure such as forming a base of a matroid or a path in a graph. We focus on the pure-exploration problem of identifying the best arm with fixed confidence, as well as a more general setting, where the structure of the answer set differs from the one of the action set. Using the recently popularized game framework, we interpret this problem as a sequential zero-sum game and develop a CombGame meta-algorithm whose instances are asymptotically optimal algorithms with finite time guarantees. In addition to comparing two families of learners to instantiate our meta-algorithm, the main contribution of our work is a specific oracle efficient instance for best-arm identification with combinatorial actions. Based on a projection-free online learning algorithm for convex polytopes, it is the first computationally efficient algorithm which is asymptotically optimal and has competitive empirical performance.

Asymptotically Optimal Information-Directed Sampling

We introduce a computationally efficient algorithm for finite stochastic linear bandits. The approach is based on the frequentist information-directed sampling (IDS) framework, with an information gain potential that is derived directly from the asymptotic regret lower bound. We establish frequentist regret bounds, which show that the proposed algorithm is both asymptotically optimal and worst-case rate optimal in finite time. Our analysis sheds light on how IDS trades off regret and information to incrementally solve the semi-infinite concave program that defines the optimal asymptotic regret. Along the way, we uncover interesting connections towards a recently proposed two-player game approach and the Bayesian IDS algorithm.