Group Robust Preference Optimization in Reward-free RLHF

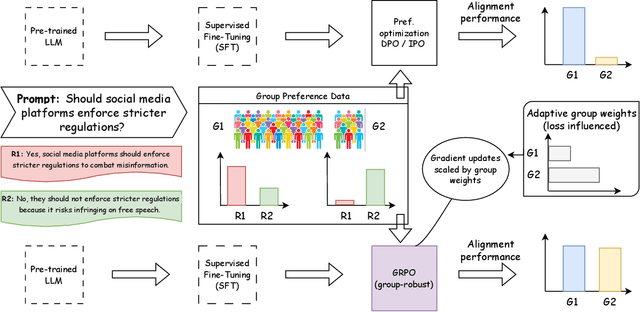
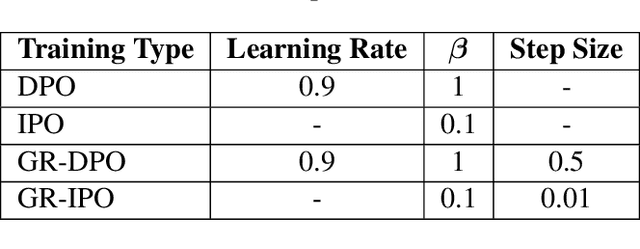
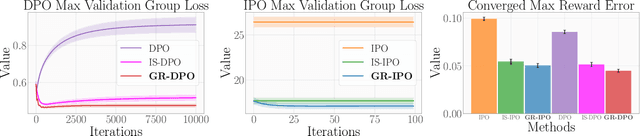
Adapting large language models (LLMs) for specific tasks usually involves fine-tuning through reinforcement learning with human feedback (RLHF) on preference data. While these data often come from diverse labelers' groups (e.g., different demographics, ethnicities, company teams, etc.), traditional RLHF approaches adopt a "one-size-fits-all" approach, i.e., they indiscriminately assume and optimize a single preference model, thus not being robust to unique characteristics and needs of the various groups. To address this limitation, we propose a novel Group Robust Preference Optimization (GRPO) method to align LLMs to individual groups' preferences robustly. Our approach builds upon reward-free direct preference optimization methods, but unlike previous approaches, it seeks a robust policy which maximizes the worst-case group performance. To achieve this, GRPO adaptively and sequentially weights the importance of different groups, prioritizing groups with worse cumulative loss. We theoretically study the feasibility of GRPO and analyze its convergence for the log-linear policy class. By fine-tuning LLMs with GRPO using diverse group-based global opinion data, we significantly improved performance for the worst-performing groups, reduced loss imbalances across groups, and improved probability accuracies compared to non-robust baselines.

Sample Efficient Reinforcement Learning from Human Feedback via Active Exploration

Preference-based feedback is important for many applications in reinforcement learning where direct evaluation of a reward function is not feasible. A notable recent example arises in reinforcement learning from human feedback (RLHF) on large language models. For many applications of RLHF, the cost of acquiring the human feedback can be substantial. In this work, we take advantage of the fact that one can often choose contexts at which to obtain human feedback in order to most efficiently identify a good policy, and formalize this as an offline contextual dueling bandit problem. We give an upper-confidence-bound style algorithm for this problem and prove a polynomial worst-case regret bound. We then provide empirical confirmation in a synthetic setting that our approach outperforms existing methods. After, we extend the setting and methodology for practical use in RLHF training of large language models. Here, our method is able to reach better performance with fewer samples of human preferences than multiple baselines on three real-world datasets.

Kernelized Offline Contextual Dueling Bandits

Preference-based feedback is important for many applications where direct evaluation of a reward function is not feasible. A notable recent example arises in reinforcement learning from human feedback on large language models. For many of these applications, the cost of acquiring the human feedback can be substantial or even prohibitive. In this work, we take advantage of the fact that often the agent can choose contexts at which to obtain human feedback in order to most efficiently identify a good policy, and introduce the offline contextual dueling bandit setting. We give an upper-confidence-bound style algorithm for this setting and prove a regret bound. We also give empirical confirmation that this method outperforms a similar strategy that uses uniformly sampled contexts.

Near-optimal Policy Identification in Active Reinforcement Learning

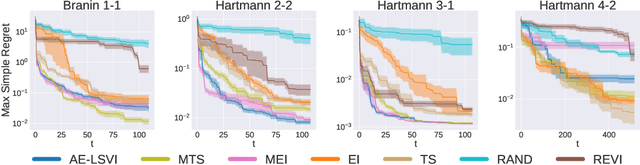
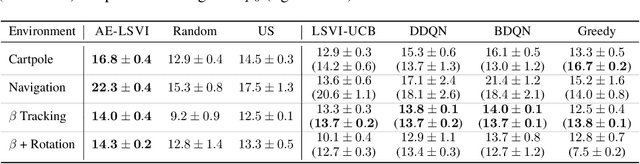
Many real-world reinforcement learning tasks require control of complex dynamical systems that involve both costly data acquisition processes and large state spaces. In cases where the transition dynamics can be readily evaluated at specified states (e.g., via a simulator), agents can operate in what is often referred to as planning with a \emph{generative model}. We propose the AE-LSVI algorithm for best-policy identification, a novel variant of the kernelized least-squares value iteration (LSVI) algorithm that combines optimism with pessimism for active exploration (AE). AE-LSVI provably identifies a near-optimal policy \emph{uniformly} over an entire state space and achieves polynomial sample complexity guarantees that are independent of the number of states. When specialized to the recently introduced offline contextual Bayesian optimization setting, our algorithm achieves improved sample complexity bounds. Experimentally, we demonstrate that AE-LSVI outperforms other RL algorithms in a variety of environments when robustness to the initial state is required.

Exploration via Planning for Information about the Optimal Trajectory

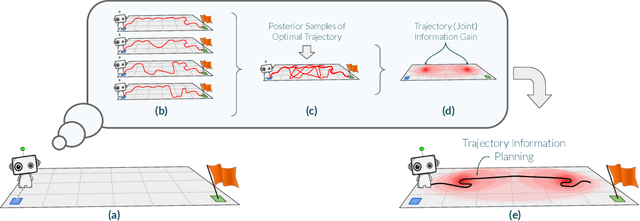
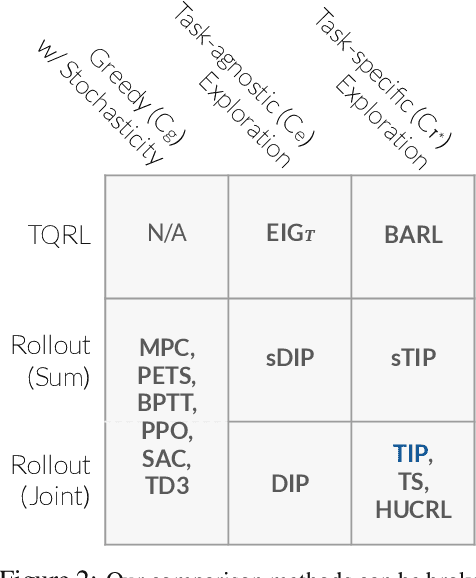
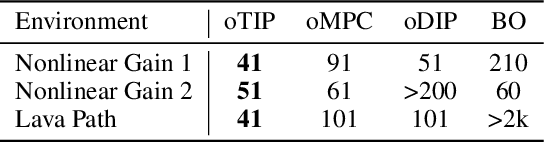
Many potential applications of reinforcement learning (RL) are stymied by the large numbers of samples required to learn an effective policy. This is especially true when applying RL to real-world control tasks, e.g. in the sciences or robotics, where executing a policy in the environment is costly. In popular RL algorithms, agents typically explore either by adding stochasticity to a reward-maximizing policy or by attempting to gather maximal information about environment dynamics without taking the given task into account. In this work, we develop a method that allows us to plan for exploration while taking both the task and the current knowledge about the dynamics into account. The key insight to our approach is to plan an action sequence that maximizes the expected information gain about the optimal trajectory for the task at hand. We demonstrate that our method learns strong policies with 2x fewer samples than strong exploration baselines and 200x fewer samples than model free methods on a diverse set of low-to-medium dimensional control tasks in both the open-loop and closed-loop control settings.

BATS: Best Action Trajectory Stitching

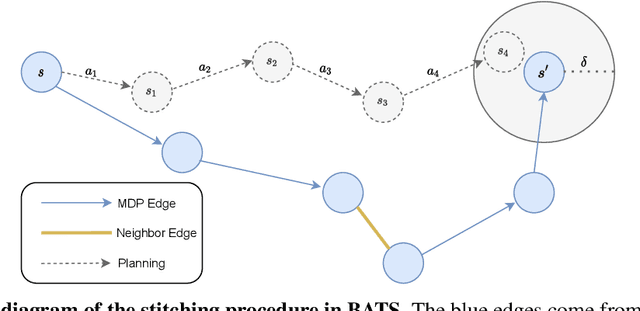
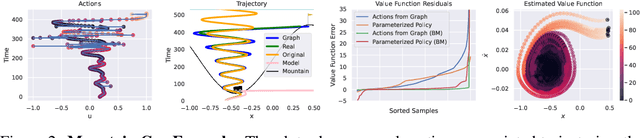
The problem of offline reinforcement learning focuses on learning a good policy from a log of environment interactions. Past efforts for developing algorithms in this area have revolved around introducing constraints to online reinforcement learning algorithms to ensure the actions of the learned policy are constrained to the logged data. In this work, we explore an alternative approach by planning on the fixed dataset directly. Specifically, we introduce an algorithm which forms a tabular Markov Decision Process (MDP) over the logged data by adding new transitions to the dataset. We do this by using learned dynamics models to plan short trajectories between states. Since exact value iteration can be performed on this constructed MDP, it becomes easy to identify which trajectories are advantageous to add to the MDP. Crucially, since most transitions in this MDP come from the logged data, trajectories from the MDP can be rolled out for long periods with confidence. We prove that this property allows one to make upper and lower bounds on the value function up to appropriate distance metrics. Finally, we demonstrate empirically how algorithms that uniformly constrain the learned policy to the entire dataset can result in unwanted behavior, and we show an example in which simply behavior cloning the optimal policy of the MDP created by our algorithm avoids this problem.

Variational autoencoders in the presence of low-dimensional data: landscape and implicit bias

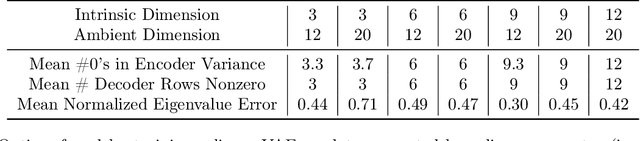
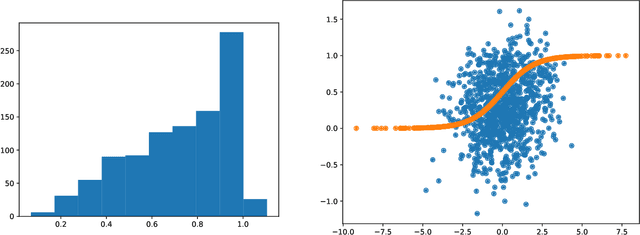
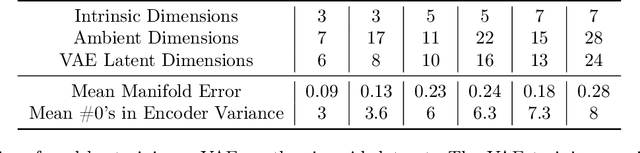
Variational Autoencoders (VAEs) are one of the most commonly used generative models, particularly for image data. A prominent difficulty in training VAEs is data that is supported on a lower dimensional manifold. Recent work by Dai and Wipf (2019) suggests that on low-dimensional data, the generator will converge to a solution with 0 variance which is correctly supported on the ground truth manifold. In this paper, via a combination of theoretical and empirical results, we show that the story is more subtle. Precisely, we show that for linear encoders/decoders, the story is mostly true and VAE training does recover a generator with support equal to the ground truth manifold, but this is due to the implicit bias of gradient descent rather than merely the VAE loss itself. In the nonlinear case, we show that the VAE training frequently learns a higher-dimensional manifold which is a superset of the ground truth manifold.

An Experimental Design Perspective on Model-Based Reinforcement Learning

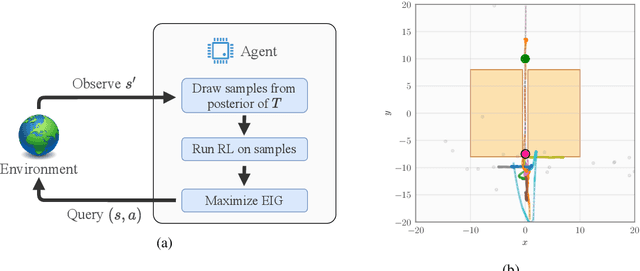
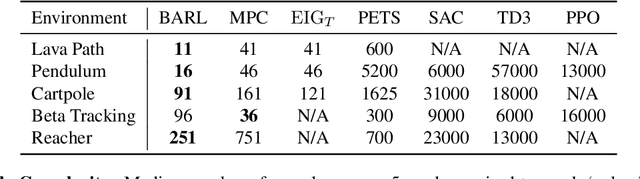
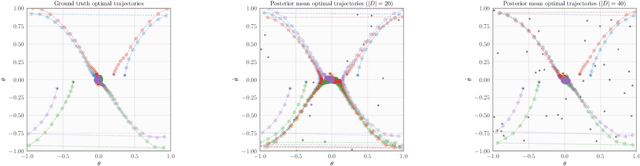
In many practical applications of RL, it is expensive to observe state transitions from the environment. For example, in the problem of plasma control for nuclear fusion, computing the next state for a given state-action pair requires querying an expensive transition function which can lead to many hours of computer simulation or dollars of scientific research. Such expensive data collection prohibits application of standard RL algorithms which usually require a large number of observations to learn. In this work, we address the problem of efficiently learning a policy while making a minimal number of state-action queries to the transition function. In particular, we leverage ideas from Bayesian optimal experimental design to guide the selection of state-action queries for efficient learning. We propose an acquisition function that quantifies how much information a state-action pair would provide about the optimal solution to a Markov decision process. At each iteration, our algorithm maximizes this acquisition function, to choose the most informative state-action pair to be queried, thus yielding a data-efficient RL approach. We experiment with a variety of simulated continuous control problems and show that our approach learns an optimal policy with up to $5$ -- $1,000\times$ less data than model-based RL baselines and $10^3$ -- $10^5\times$ less data than model-free RL baselines. We also provide several ablated comparisons which point to substantial improvements arising from the principled method of obtaining data.

Representational aspects of depth and conditioning in normalizing flows

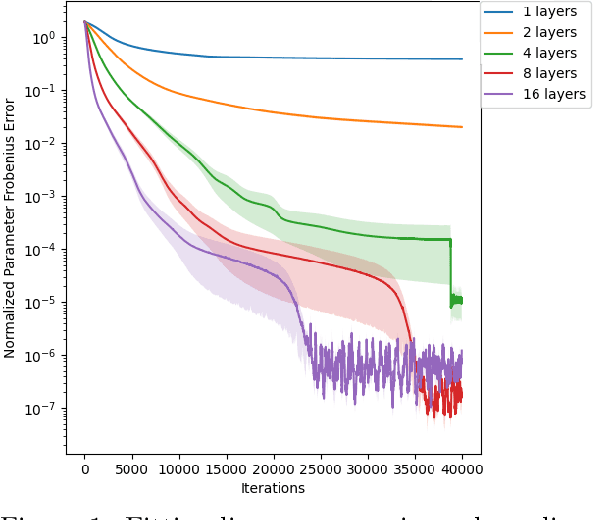
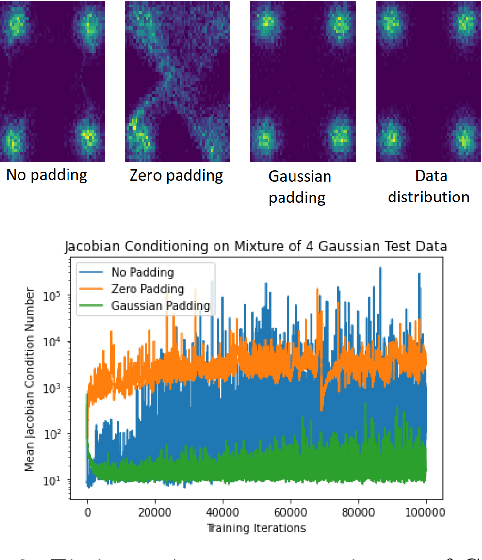
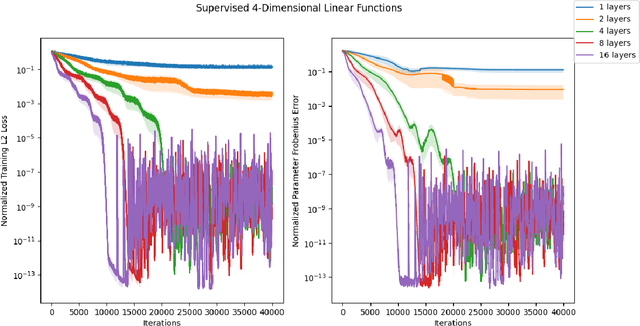
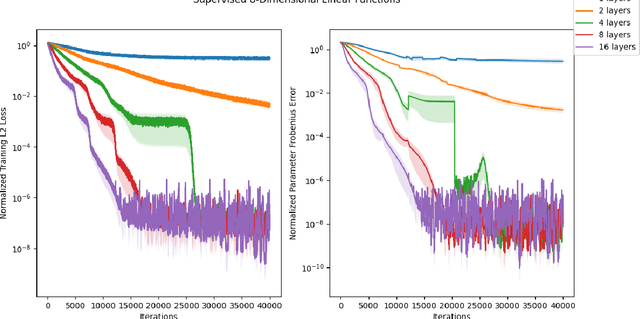
Normalizing flows are among the most popular paradigms in generative modeling, especially for images, primarily because we can efficiently evaluate the likelihood of a data point. Normalizing flows also come with difficulties: models which produce good samples typically need to be extremely deep -- which comes with accompanying vanishing/exploding gradient problems. Relatedly, they are often poorly conditioned since typical training data like images intuitively are lower-dimensional, and the learned maps often have Jacobians that are close to being singular. In our paper, we tackle representational aspects around depth and conditioning of normalizing flows -- both for general invertible architectures, and for a particular common architecture -- affine couplings. For general invertible architectures, we prove that invertibility comes at a cost in terms of depth: we show examples where a much deeper normalizing flow model may need to be used to match the performance of a non-invertible generator. For affine couplings, we first show that the choice of partitions isn't a likely bottleneck for depth: we show that any invertible linear map (and hence a permutation) can be simulated by a constant number of affine coupling layers, using a fixed partition. This shows that the extra flexibility conferred by 1x1 convolution layers, as in GLOW, can in principle be simulated by increasing the size by a constant factor. Next, in terms of conditioning, we show that affine couplings are universal approximators -- provided the Jacobian of the model is allowed to be close to singular. We furthermore empirically explore the benefit of different kinds of padding -- a common strategy for improving conditioning -- on both synthetic and real-life datasets.

Neural Dynamical Systems: Balancing Structure and Flexibility in Physical Prediction

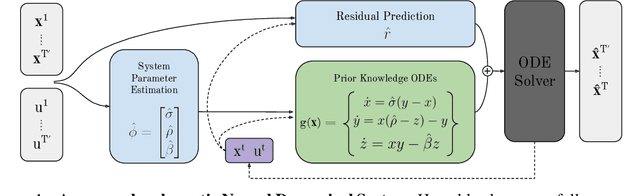
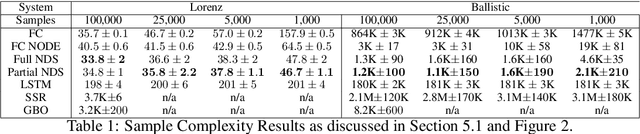
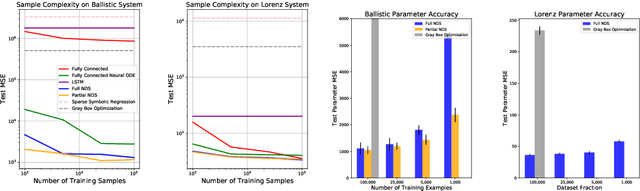
We introduce Neural Dynamical Systems (NDS), a method of learning dynamical models in various gray-box settings which incorporates prior knowledge in the form of systems of ordinary differential equations. NDS uses neural networks to estimate free parameters of the system, predicts residual terms, and numerically integrates over time to predict future states. A key insight is that many real dynamic systems of interest are hard to model because the dynamics may vary across rollouts. We mitigate this problem by taking a trajectory of prior states as the input to NDS and train it to re-estimate system parameters using the preceding trajectory. We find that NDS learns dynamics with higher accuracy and fewer samples than a variety of deep learning methods that do not incorporate the prior knowledge and methods from the system identification literature which do. We demonstrate these advantages first on synthetic dynamical systems and then on real data captured from deuterium shots from a nuclear fusion reactor.