Variational autoencoders in the presence of low-dimensional data: landscape and implicit bias

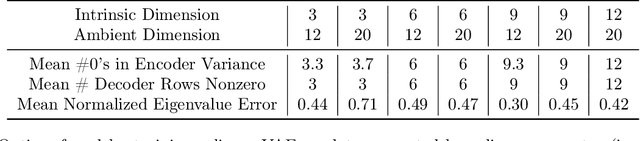
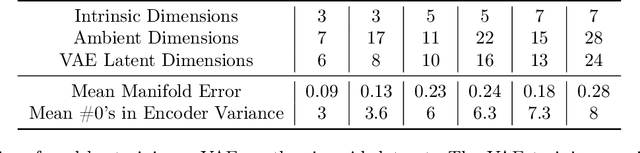
Variational Autoencoders (VAEs) are one of the most commonly used generative models, particularly for image data. A prominent difficulty in training VAEs is data that is supported on a lower dimensional manifold. Recent work by Dai and Wipf (2019) suggests that on low-dimensional data, the generator will converge to a solution with 0 variance which is correctly supported on the ground truth manifold. In this paper, via a combination of theoretical and empirical results, we show that the story is more subtle. Precisely, we show that for linear encoders/decoders, the story is mostly true and VAE training does recover a generator with support equal to the ground truth manifold, but this is due to the implicit bias of gradient descent rather than merely the VAE loss itself. In the nonlinear case, we show that the VAE training frequently learns a higher-dimensional manifold which is a superset of the ground truth manifold.