Full Shot Predictions for the DIII-D Tokamak via Deep Recurrent Networks

Although tokamaks are one of the most promising devices for realizing nuclear fusion as an energy source, there are still key obstacles when it comes to understanding the dynamics of the plasma and controlling it. As such, it is crucial that high quality models are developed to assist in overcoming these obstacles. In this work, we take an entirely data driven approach to learn such a model. In particular, we use historical data from the DIII-D tokamak to train a deep recurrent network that is able to predict the full time evolution of plasma discharges (or "shots"). Following this, we investigate how different training and inference procedures affect the quality and calibration of the shot predictions.

PID-Inspired Inductive Biases for Deep Reinforcement Learning in Partially Observable Control Tasks

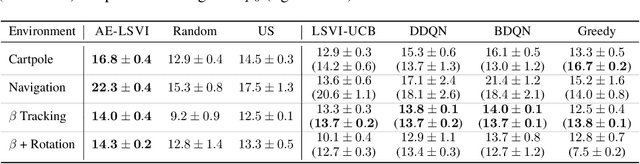
Deep reinforcement learning (RL) has shown immense potential for learning to control systems through data alone. However, one challenge deep RL faces is that the full state of the system is often not observable. When this is the case, the policy needs to leverage the history of observations to infer the current state. At the same time, differences between the training and testing environments makes it critical for the policy not to overfit to the sequence of observations it sees at training time. As such, there is an important balancing act between having the history encoder be flexible enough to extract relevant information, yet be robust to changes in the environment. To strike this balance, we look to the PID controller for inspiration. We assert the PID controller's success shows that only summing and differencing are needed to accumulate information over time for many control tasks. Following this principle, we propose two architectures for encoding history: one that directly uses PID features and another that extends these core ideas and can be used in arbitrary control tasks. When compared with prior approaches, our encoders produce policies that are often more robust and achieve better performance on a variety of tracking tasks. Going beyond tracking tasks, our policies achieve 1.7x better performance on average over previous state-of-the-art methods on a suite of high dimensional control tasks.

Near-optimal Policy Identification in Active Reinforcement Learning

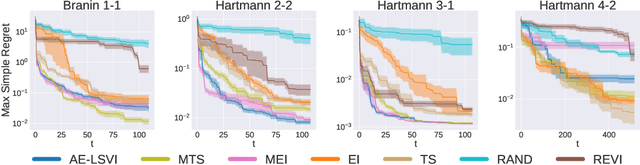
Many real-world reinforcement learning tasks require control of complex dynamical systems that involve both costly data acquisition processes and large state spaces. In cases where the transition dynamics can be readily evaluated at specified states (e.g., via a simulator), agents can operate in what is often referred to as planning with a \emph{generative model}. We propose the AE-LSVI algorithm for best-policy identification, a novel variant of the kernelized least-squares value iteration (LSVI) algorithm that combines optimism with pessimism for active exploration (AE). AE-LSVI provably identifies a near-optimal policy \emph{uniformly} over an entire state space and achieves polynomial sample complexity guarantees that are independent of the number of states. When specialized to the recently introduced offline contextual Bayesian optimization setting, our algorithm achieves improved sample complexity bounds. Experimentally, we demonstrate that AE-LSVI outperforms other RL algorithms in a variety of environments when robustness to the initial state is required.

Exploration via Planning for Information about the Optimal Trajectory

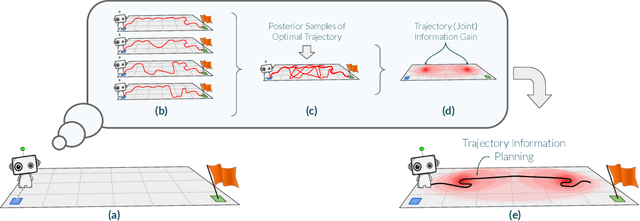
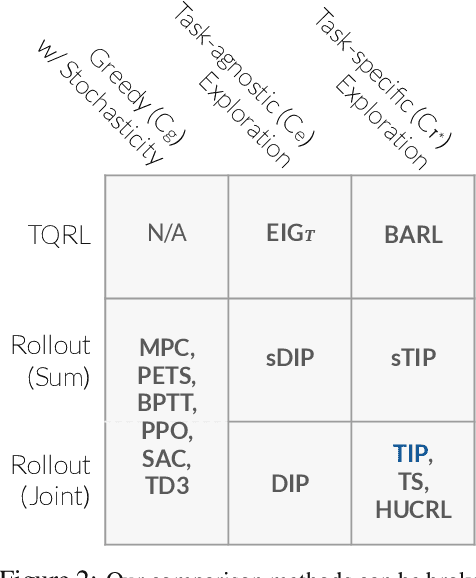
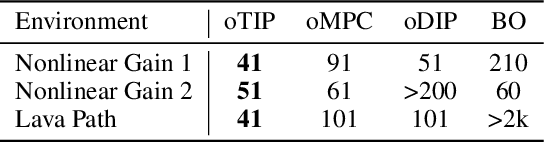
Many potential applications of reinforcement learning (RL) are stymied by the large numbers of samples required to learn an effective policy. This is especially true when applying RL to real-world control tasks, e.g. in the sciences or robotics, where executing a policy in the environment is costly. In popular RL algorithms, agents typically explore either by adding stochasticity to a reward-maximizing policy or by attempting to gather maximal information about environment dynamics without taking the given task into account. In this work, we develop a method that allows us to plan for exploration while taking both the task and the current knowledge about the dynamics into account. The key insight to our approach is to plan an action sequence that maximizes the expected information gain about the optimal trajectory for the task at hand. We demonstrate that our method learns strong policies with 2x fewer samples than strong exploration baselines and 200x fewer samples than model free methods on a diverse set of low-to-medium dimensional control tasks in both the open-loop and closed-loop control settings.

How Useful are Gradients for OOD Detection Really?

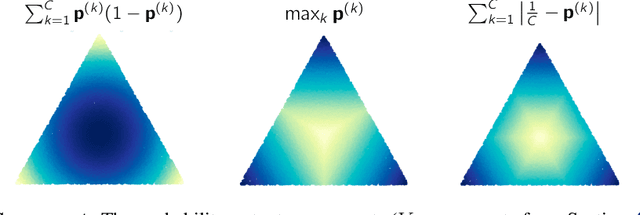
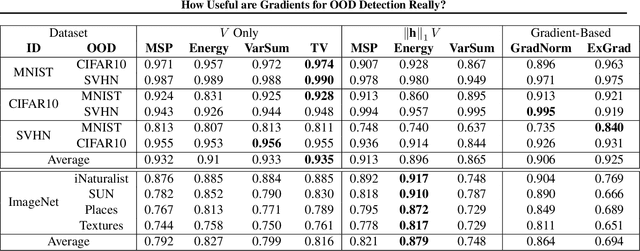
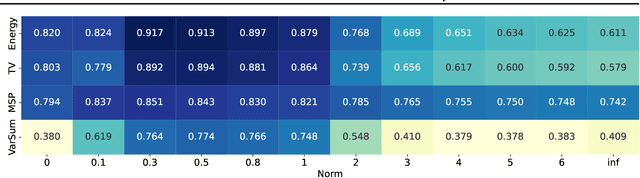
One critical challenge in deploying highly performant machine learning models in real-life applications is out of distribution (OOD) detection. Given a predictive model which is accurate on in distribution (ID) data, an OOD detection system will further equip the model with the option to defer prediction when the input is novel and the model has little confidence in prediction. There has been some recent interest in utilizing the gradient information in pre-trained models for OOD detection. While these methods have shown competitive performance, there are misconceptions about the true mechanism underlying them, which conflate their performance with the necessity of gradients. In this work, we provide an in-depth analysis and comparison of gradient based methods and elucidate the key components that warrant their OOD detection performance. We further propose a general, non-gradient based method of OOD detection which improves over previous baselines in both performance and computational efficiency.

BATS: Best Action Trajectory Stitching

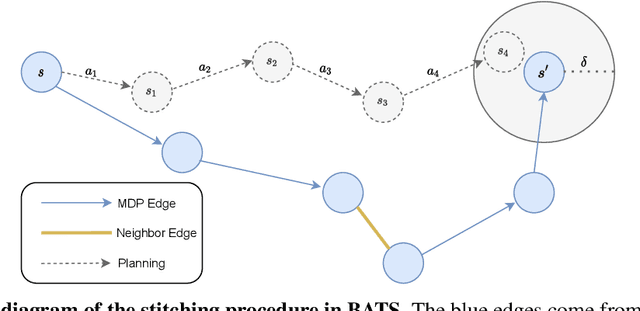
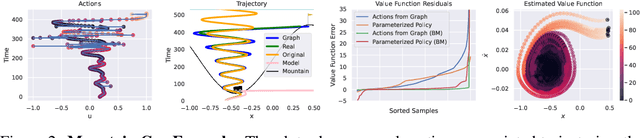
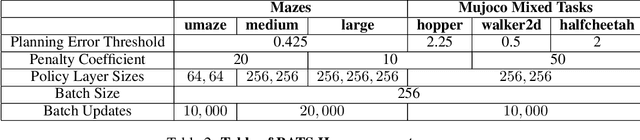
The problem of offline reinforcement learning focuses on learning a good policy from a log of environment interactions. Past efforts for developing algorithms in this area have revolved around introducing constraints to online reinforcement learning algorithms to ensure the actions of the learned policy are constrained to the logged data. In this work, we explore an alternative approach by planning on the fixed dataset directly. Specifically, we introduce an algorithm which forms a tabular Markov Decision Process (MDP) over the logged data by adding new transitions to the dataset. We do this by using learned dynamics models to plan short trajectories between states. Since exact value iteration can be performed on this constructed MDP, it becomes easy to identify which trajectories are advantageous to add to the MDP. Crucially, since most transitions in this MDP come from the logged data, trajectories from the MDP can be rolled out for long periods with confidence. We prove that this property allows one to make upper and lower bounds on the value function up to appropriate distance metrics. Finally, we demonstrate empirically how algorithms that uniformly constrain the learned policy to the entire dataset can result in unwanted behavior, and we show an example in which simply behavior cloning the optimal policy of the MDP created by our algorithm avoids this problem.

Uncertainty Toolbox: an Open-Source Library for Assessing, Visualizing, and Improving Uncertainty Quantification

With increasing deployment of machine learning systems in various real-world tasks, there is a greater need for accurate quantification of predictive uncertainty. While the common goal in uncertainty quantification (UQ) in machine learning is to approximate the true distribution of the target data, many works in UQ tend to be disjoint in the evaluation metrics utilized, and disparate implementations for each metric lead to numerical results that are not directly comparable across different works. To address this, we introduce Uncertainty Toolbox, an open-source python library that helps to assess, visualize, and improve UQ. Uncertainty Toolbox additionally provides pedagogical resources, such as a glossary of key terms and an organized collection of key paper references. We hope that this toolbox is useful for accelerating and uniting research efforts in uncertainty in machine learning.

Beyond Pinball Loss: Quantile Methods for Calibrated Uncertainty Quantification

Among the many ways of quantifying uncertainty in a regression setting, specifying the full quantile function is attractive, as quantiles are amenable to interpretation and evaluation. A model that predicts the true conditional quantiles for each input, at all quantile levels, presents a correct and efficient representation of the underlying uncertainty. To achieve this, many current quantile-based methods focus on optimizing the so-called pinball loss. However, this loss restricts the scope of applicable regression models, limits the ability to target many desirable properties (e.g. calibration, sharpness, centered intervals), and may produce poor conditional quantiles. In this work, we develop new quantile methods that address these shortcomings. In particular, we propose methods that can apply to any class of regression model, allow for selecting a Pareto-optimal trade-off between calibration and sharpness, optimize for calibration of centered intervals, and produce more accurate conditional quantiles. We provide a thorough experimental evaluation of our methods, which includes a high dimensional uncertainty quantification task in nuclear fusion.

Neural Dynamical Systems: Balancing Structure and Flexibility in Physical Prediction

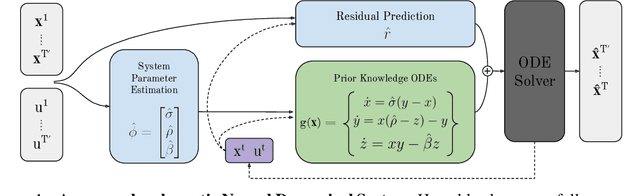
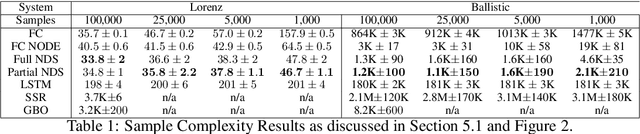
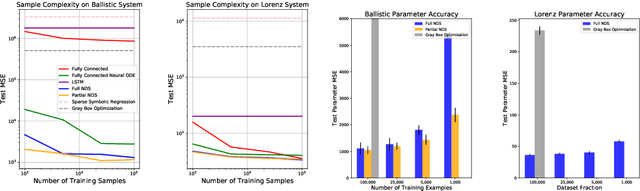
We introduce Neural Dynamical Systems (NDS), a method of learning dynamical models in various gray-box settings which incorporates prior knowledge in the form of systems of ordinary differential equations. NDS uses neural networks to estimate free parameters of the system, predicts residual terms, and numerically integrates over time to predict future states. A key insight is that many real dynamic systems of interest are hard to model because the dynamics may vary across rollouts. We mitigate this problem by taking a trajectory of prior states as the input to NDS and train it to re-estimate system parameters using the preceding trajectory. We find that NDS learns dynamics with higher accuracy and fewer samples than a variety of deep learning methods that do not incorporate the prior knowledge and methods from the system identification literature which do. We demonstrate these advantages first on synthetic dynamical systems and then on real data captured from deuterium shots from a nuclear fusion reactor.

Offline Contextual Bayesian Optimization for Nuclear Fusion

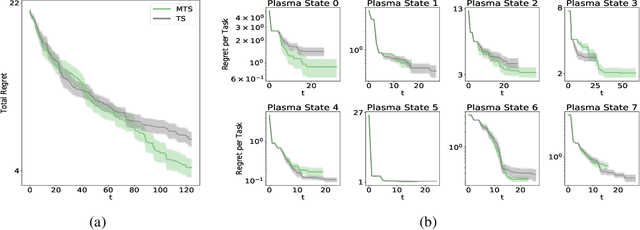
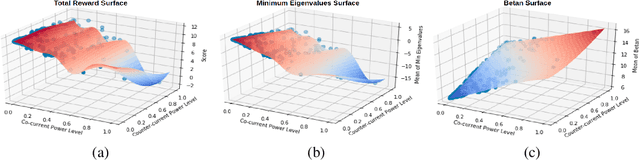
Nuclear fusion is regarded as the energy of the future since it presents the possibility of unlimited clean energy. One obstacle in utilizing fusion as a feasible energy source is the stability of the reaction. Ideally, one would have a controller for the reactor that makes actions in response to the current state of the plasma in order to prolong the reaction as long as possible. In this work, we make preliminary steps to learning such a controller. Since learning on a real world reactor is infeasible, we tackle this problem by attempting to learn optimal controls offline via a simulator, where the state of the plasma can be explicitly set. In particular, we introduce a theoretically grounded Bayesian optimization algorithm that recommends a state and action pair to evaluate at every iteration and show that this results in more efficient use of the simulator.