Near-optimal Policy Identification in Active Reinforcement Learning
Paper and Code
Dec 19, 2022
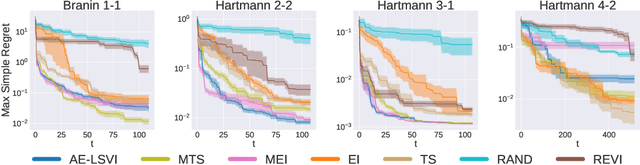
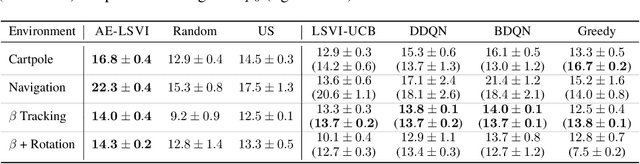

Many real-world reinforcement learning tasks require control of complex dynamical systems that involve both costly data acquisition processes and large state spaces. In cases where the transition dynamics can be readily evaluated at specified states (e.g., via a simulator), agents can operate in what is often referred to as planning with a \emph{generative model}. We propose the AE-LSVI algorithm for best-policy identification, a novel variant of the kernelized least-squares value iteration (LSVI) algorithm that combines optimism with pessimism for active exploration (AE). AE-LSVI provably identifies a near-optimal policy \emph{uniformly} over an entire state space and achieves polynomial sample complexity guarantees that are independent of the number of states. When specialized to the recently introduced offline contextual Bayesian optimization setting, our algorithm achieves improved sample complexity bounds. Experimentally, we demonstrate that AE-LSVI outperforms other RL algorithms in a variety of environments when robustness to the initial state is required.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge