How does ion temperature gradient turbulence depend on magnetic geometry? Insights from data and machine learning

Magnetic geometry has a significant effect on the level of turbulent transport in fusion plasmas. Here, we model and analyze this dependence using multiple machine learning methods and a dataset of > 200,000 nonlinear simulations of ion-temperature-gradient turbulence in diverse non-axisymmetric geometries. The dataset is generated using a large collection of both optimized and randomly generated stellarator equilibria. At fixed gradients, the turbulent heat flux varies between geometries by several orders of magnitude. Trends are apparent among the configurations with particularly high or low heat flux. Regression and classification techniques from machine learning are then applied to extract patterns in the dataset. Due to a symmetry of the gyrokinetic equation, the heat flux and regressions thereof should be invariant to translations of the raw features in the parallel coordinate, similar to translation invariance in computer vision applications. Multiple regression models including convolutional neural networks (CNNs) and decision trees can achieve reasonable predictive power for the heat flux in held-out test configurations, with highest accuracy for the CNNs. Using Spearman correlation, sequential feature selection, and Shapley values to measure feature importance, it is consistently found that the most important geometric lever on the heat flux is the flux surface compression in regions of bad curvature. The second most important feature relates to the magnitude of geodesic curvature. These two features align remarkably with surrogates that have been proposed based on theory, while the methods here allow a natural extension to more features for increased accuracy. The dataset, released with this publication, may also be used to test other proposed surrogates, and we find many previously published proxies do correlate well with both the heat flux and stability boundary.

Exploration via Planning for Information about the Optimal Trajectory

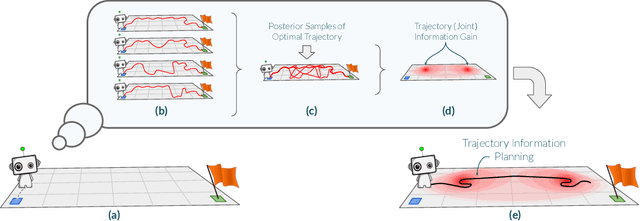
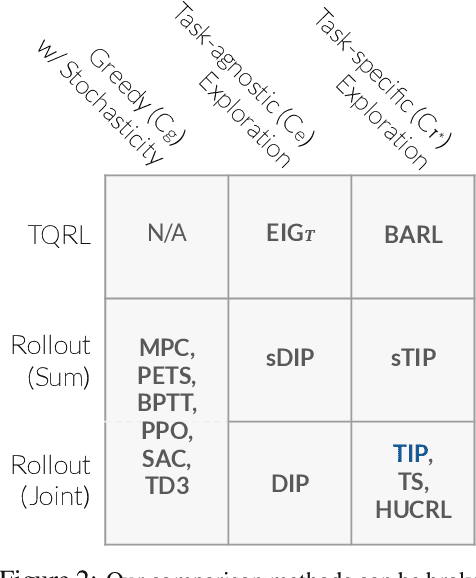
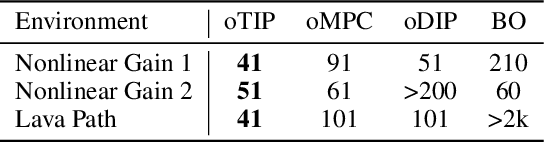
Many potential applications of reinforcement learning (RL) are stymied by the large numbers of samples required to learn an effective policy. This is especially true when applying RL to real-world control tasks, e.g. in the sciences or robotics, where executing a policy in the environment is costly. In popular RL algorithms, agents typically explore either by adding stochasticity to a reward-maximizing policy or by attempting to gather maximal information about environment dynamics without taking the given task into account. In this work, we develop a method that allows us to plan for exploration while taking both the task and the current knowledge about the dynamics into account. The key insight to our approach is to plan an action sequence that maximizes the expected information gain about the optimal trajectory for the task at hand. We demonstrate that our method learns strong policies with 2x fewer samples than strong exploration baselines and 200x fewer samples than model free methods on a diverse set of low-to-medium dimensional control tasks in both the open-loop and closed-loop control settings.