Neural Dynamical Systems: Balancing Structure and Flexibility in Physical Prediction

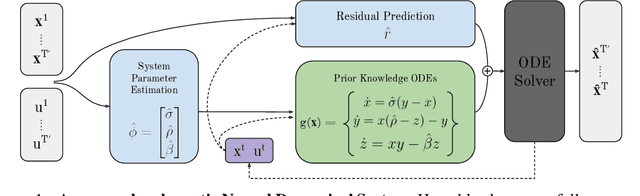
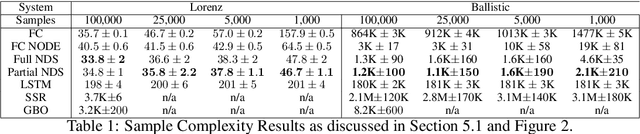
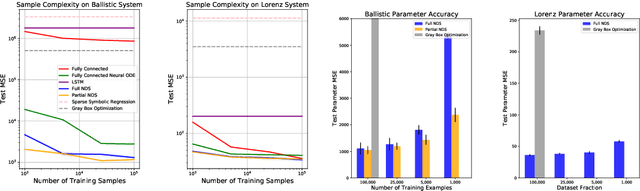
We introduce Neural Dynamical Systems (NDS), a method of learning dynamical models in various gray-box settings which incorporates prior knowledge in the form of systems of ordinary differential equations. NDS uses neural networks to estimate free parameters of the system, predicts residual terms, and numerically integrates over time to predict future states. A key insight is that many real dynamic systems of interest are hard to model because the dynamics may vary across rollouts. We mitigate this problem by taking a trajectory of prior states as the input to NDS and train it to re-estimate system parameters using the preceding trajectory. We find that NDS learns dynamics with higher accuracy and fewer samples than a variety of deep learning methods that do not incorporate the prior knowledge and methods from the system identification literature which do. We demonstrate these advantages first on synthetic dynamical systems and then on real data captured from deuterium shots from a nuclear fusion reactor.