An Experimental Design Perspective on Model-Based Reinforcement Learning
Paper and Code
Dec 09, 2021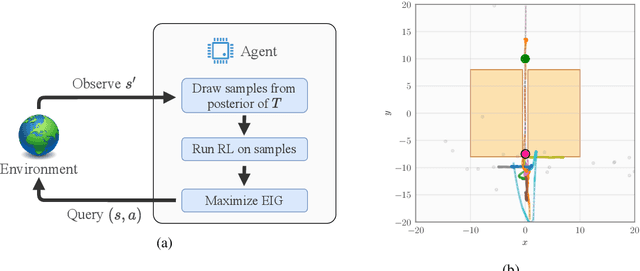
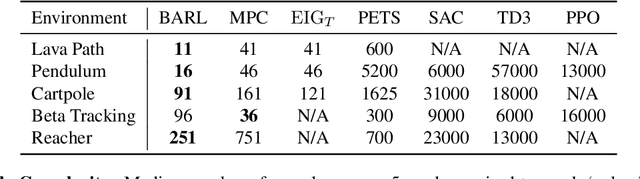
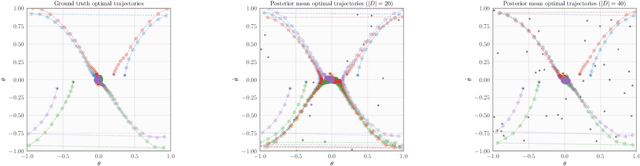

In many practical applications of RL, it is expensive to observe state transitions from the environment. For example, in the problem of plasma control for nuclear fusion, computing the next state for a given state-action pair requires querying an expensive transition function which can lead to many hours of computer simulation or dollars of scientific research. Such expensive data collection prohibits application of standard RL algorithms which usually require a large number of observations to learn. In this work, we address the problem of efficiently learning a policy while making a minimal number of state-action queries to the transition function. In particular, we leverage ideas from Bayesian optimal experimental design to guide the selection of state-action queries for efficient learning. We propose an acquisition function that quantifies how much information a state-action pair would provide about the optimal solution to a Markov decision process. At each iteration, our algorithm maximizes this acquisition function, to choose the most informative state-action pair to be queried, thus yielding a data-efficient RL approach. We experiment with a variety of simulated continuous control problems and show that our approach learns an optimal policy with up to $5$ -- $1,000\times$ less data than model-based RL baselines and $10^3$ -- $10^5\times$ less data than model-free RL baselines. We also provide several ablated comparisons which point to substantial improvements arising from the principled method of obtaining data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge