Representational aspects of depth and conditioning in normalizing flows

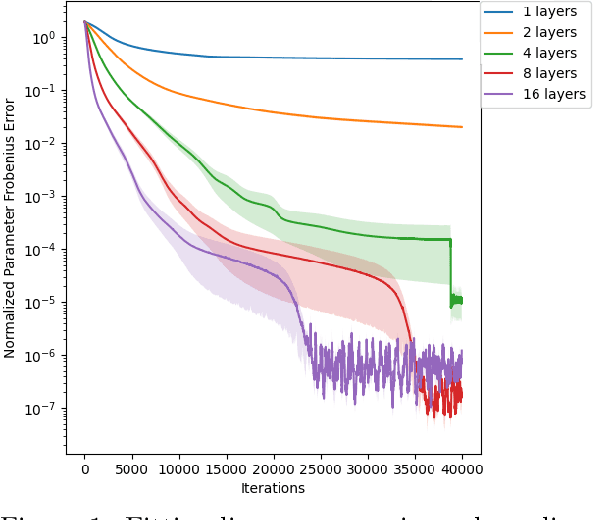
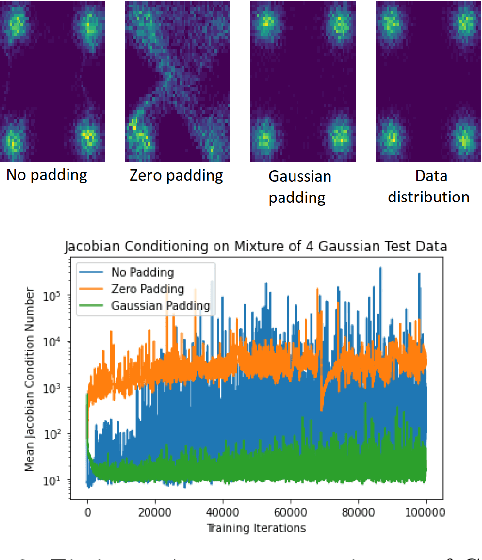
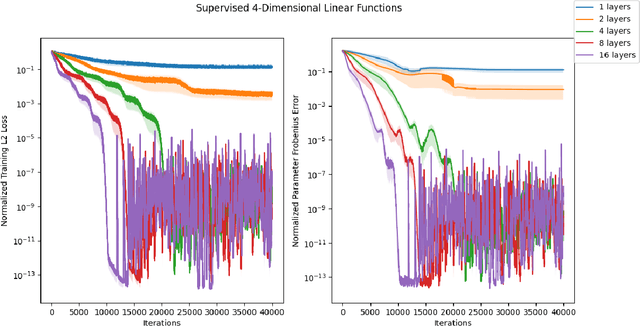
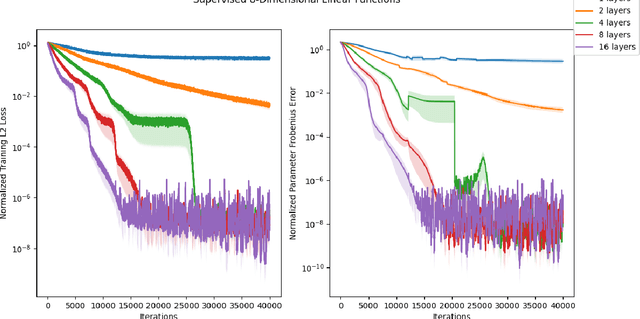
Normalizing flows are among the most popular paradigms in generative modeling, especially for images, primarily because we can efficiently evaluate the likelihood of a data point. Normalizing flows also come with difficulties: models which produce good samples typically need to be extremely deep -- which comes with accompanying vanishing/exploding gradient problems. Relatedly, they are often poorly conditioned since typical training data like images intuitively are lower-dimensional, and the learned maps often have Jacobians that are close to being singular. In our paper, we tackle representational aspects around depth and conditioning of normalizing flows -- both for general invertible architectures, and for a particular common architecture -- affine couplings. For general invertible architectures, we prove that invertibility comes at a cost in terms of depth: we show examples where a much deeper normalizing flow model may need to be used to match the performance of a non-invertible generator. For affine couplings, we first show that the choice of partitions isn't a likely bottleneck for depth: we show that any invertible linear map (and hence a permutation) can be simulated by a constant number of affine coupling layers, using a fixed partition. This shows that the extra flexibility conferred by 1x1 convolution layers, as in GLOW, can in principle be simulated by increasing the size by a constant factor. Next, in terms of conditioning, we show that affine couplings are universal approximators -- provided the Jacobian of the model is allowed to be close to singular. We furthermore empirically explore the benefit of different kinds of padding -- a common strategy for improving conditioning -- on both synthetic and real-life datasets.