Autoregressive Large Language Models are Computationally Universal

We show that autoregressive decoding of a transformer-based language model can realize universal computation, without external intervention or modification of the model's weights. Establishing this result requires understanding how a language model can process arbitrarily long inputs using a bounded context. For this purpose, we consider a generalization of autoregressive decoding where, given a long input, emitted tokens are appended to the end of the sequence as the context window advances. We first show that the resulting system corresponds to a classical model of computation, a Lag system, that has long been known to be computationally universal. By leveraging a new proof, we show that a universal Turing machine can be simulated by a Lag system with 2027 production rules. We then investigate whether an existing large language model can simulate the behaviour of such a universal Lag system. We give an affirmative answer by showing that a single system-prompt can be developed for gemini-1.5-pro-001 that drives the model, under deterministic (greedy) decoding, to correctly apply each of the 2027 production rules. We conclude that, by the Church-Turing thesis, prompted gemini-1.5-pro-001 with extended autoregressive (greedy) decoding is a general purpose computer.

Managing Temporal Resolution in Continuous Value Estimation: A Fundamental Trade-off

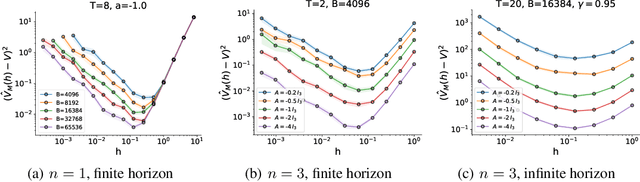
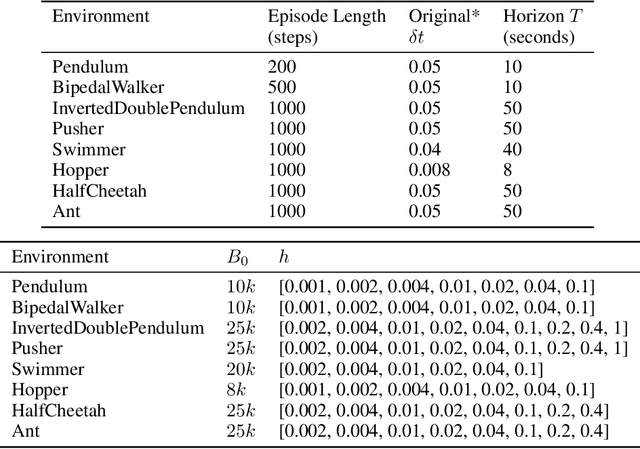
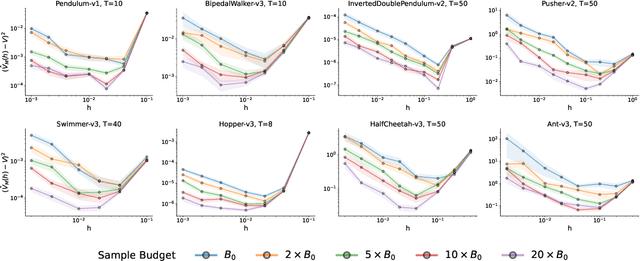
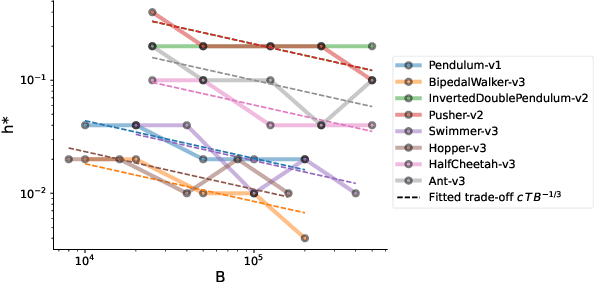
A default assumption in reinforcement learning and optimal control is that experience arrives at discrete time points on a fixed clock cycle. Many applications, however, involve continuous systems where the time discretization is not fixed but instead can be managed by a learning algorithm. By analyzing Monte-Carlo value estimation for LQR systems in both finite-horizon and infinite-horizon settings, we uncover a fundamental trade-off between approximation and statistical error in value estimation. Importantly, these two errors behave differently with respect to time discretization, which implies that there is an optimal choice for the temporal resolution that depends on the data budget. These findings show how adapting the temporal resolution can provably improve value estimation quality in LQR systems from finite data. Empirically, we demonstrate the trade-off in numerical simulations of LQR instances and several non-linear environments.

To Compute or not to Compute? Adaptive Smart Sensing in Resource-Constrained Edge Computing

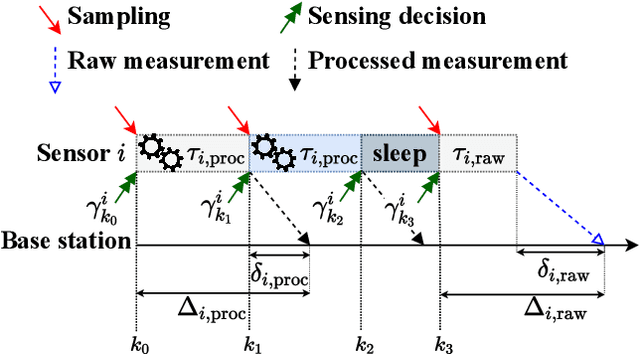
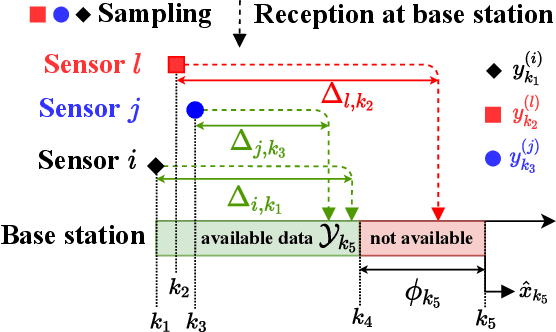
We consider a network of smart sensors for edge computing application that sample a signal of interest and send updates to a base station for remote global monitoring. Sensors are equipped with sensing and compute, and can either send raw data or process them on-board before transmission. Limited hardware resources at the edge generate a fundamental latency-accuracy trade-off: raw measurements are inaccurate but timely, whereas accurate processed updates are available after computational delay. Also, if sensor on-board processing entails data compression, latency caused by wireless communication might be higher for raw measurements. Hence, one needs to decide when sensors should transmit raw measurements or rely on local processing to maximize overall network performance. To tackle this sensing design problem, we model an estimation-theoretic optimization framework that embeds computation and communication delays, and propose a Reinforcement Learning-based approach to dynamically allocate computational resources at each sensor. Effectiveness of our proposed approach is validated through numerical simulations with case studies motivated by the Internet of Drones and self-driving vehicles.

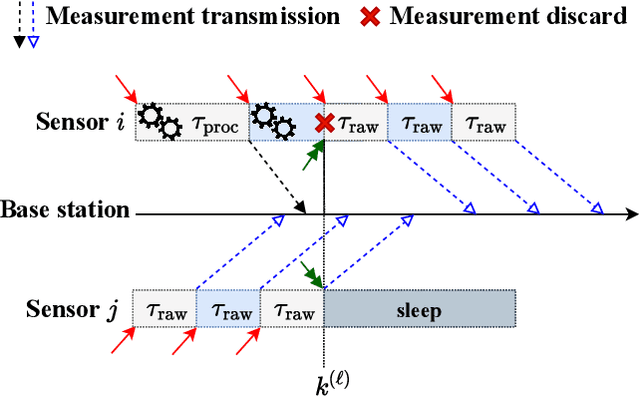
A Reinforcement Learning Approach to Sensing Design in Resource-Constrained Wireless Networked Control Systems

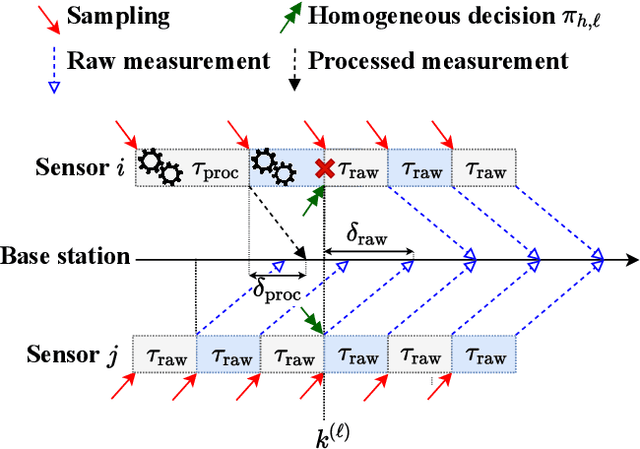
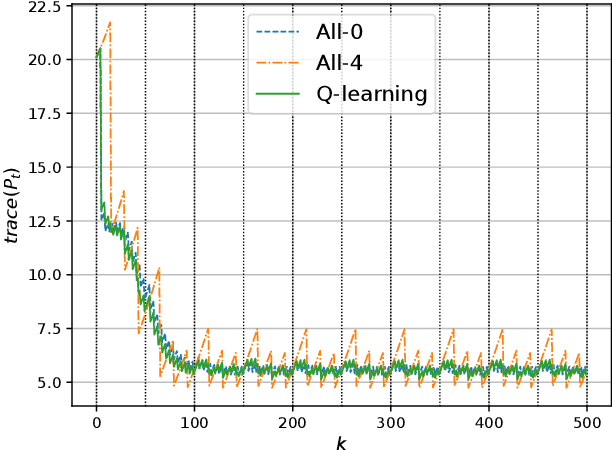
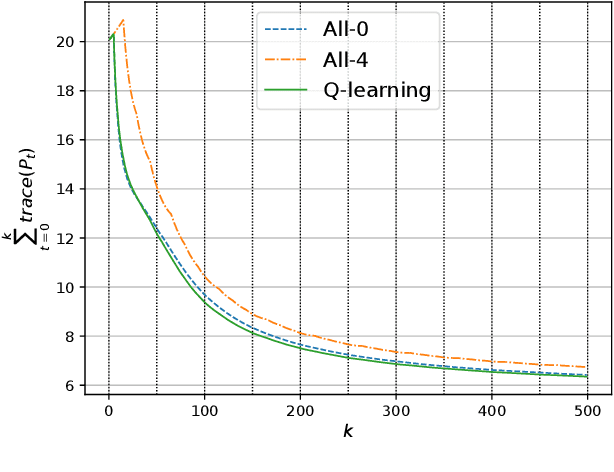
In this paper, we consider a wireless network of smart sensors (agents) that monitor a dynamical process and send measurements to a base station that performs global monitoring and decision-making. Smart sensors are equipped with both sensing and computation, and can either send raw measurements or process them prior to transmission. Constrained agent resources raise a fundamental latency-accuracy trade-off. On the one hand, raw measurements are inaccurate but fast to produce. On the other hand, data processing on resource-constrained platforms generates accurate measurements at the cost of non-negligible computation latency. Further, if processed data are also compressed, latency caused by wireless communication might be higher for raw measurements. Hence, it is challenging to decide when and where sensors in the network should transmit raw measurements or leverage time-consuming local processing. To tackle this design problem, we propose a Reinforcement Learning approach to learn an efficient policy that dynamically decides when measurements are to be processed at each sensor. Effectiveness of our proposed approach is validated through a numerical simulation with case study on smart sensing motivated by the Internet of Drones.

Estimating Koopman operators for nonlinear dynamical systems: a nonparametric approach

The Koopman operator is a mathematical tool that allows for a linear description of non-linear systems, but working in infinite dimensional spaces. Dynamic Mode Decomposition and Extended Dynamic Mode Decomposition are amongst the most popular finite dimensional approximation. In this paper we capture their core essence as a dual version of the same framework, incorporating them into the Kernel framework. To do so, we leverage the RKHS as a suitable space for learning the Koopman dynamics, thanks to its intrinsic finite-dimensional nature, shaped by data. We finally establish a strong link between kernel methods and Koopman operators, leading to the estimation of the latter through Kernel functions. We provide also simulations for comparison with standard procedures.