Almost Free: Self-concordance in Natural Exponential Families and an Application to Bandits

We prove that single-parameter natural exponential families with subexponential tails are self-concordant with polynomial-sized parameters. For subgaussian natural exponential families we establish an exact characterization of the growth rate of the self-concordance parameter. Applying these findings to bandits allows us to fill gaps in the literature: We show that optimistic algorithms for generalized linear bandits enjoy regret bounds that are both second-order (scale with the variance of the optimal arm's reward distribution) and free of an exponential dependence on the bound of the problem parameter in the leading term. To the best of our knowledge, ours is the first regret bound for generalized linear bandits with subexponential tails, broadening the class of problems to include Poisson, exponential and gamma bandits.

Switching the Loss Reduces the Cost in Batch Reinforcement Learning

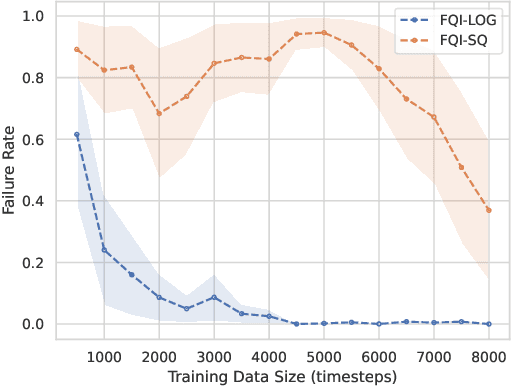
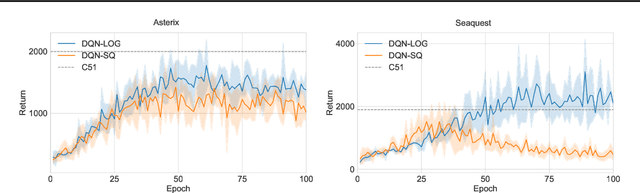
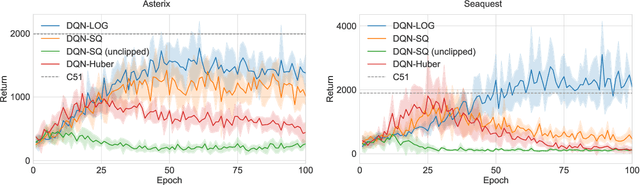
We propose training fitted Q-iteration with log-loss (FQI-LOG) for batch reinforcement learning (RL). We show that the number of samples needed to learn a near-optimal policy with FQI-LOG scales with the accumulated cost of the optimal policy, which is zero in problems where acting optimally achieves the goal and incurs no cost. In doing so, we provide a general framework for proving $\textit{small-cost}$ bounds, i.e. bounds that scale with the optimal achievable cost, in batch RL. Moreover, we empirically verify that FQI-LOG uses fewer samples than FQI trained with squared loss on problems where the optimal policy reliably achieves the goal.

Exploration via linearly perturbed loss minimisation

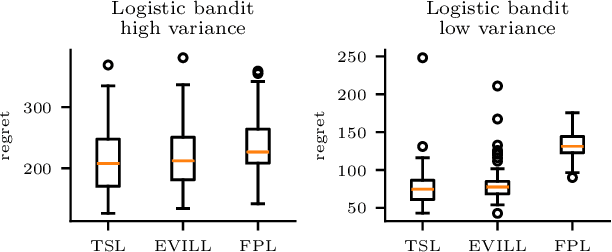
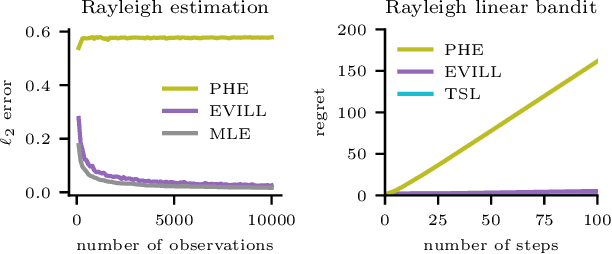
We introduce exploration via linear loss perturbations (EVILL), a randomised exploration method for structured stochastic bandit problems that works by solving for the minimiser of a linearly perturbed regularised negative log-likelihood function. We show that, for the case of generalised linear bandits, EVILL reduces to perturbed history exploration (PHE), a method where exploration is done by training on randomly perturbed rewards. In doing so, we provide a simple and clean explanation of when and why random reward perturbations give rise to good bandit algorithms. With the data-dependent perturbations we propose, not present in previous PHE-type methods, EVILL is shown to match the performance of Thompson-sampling-style parameter-perturbation methods, both in theory and in practice. Moreover, we show an example outside of generalised linear bandits where PHE leads to inconsistent estimates, and thus linear regret, while EVILL remains performant. Like PHE, EVILL can be implemented in just a few lines of code.

Managing Temporal Resolution in Continuous Value Estimation: A Fundamental Trade-off

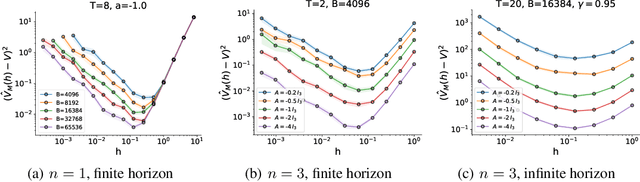
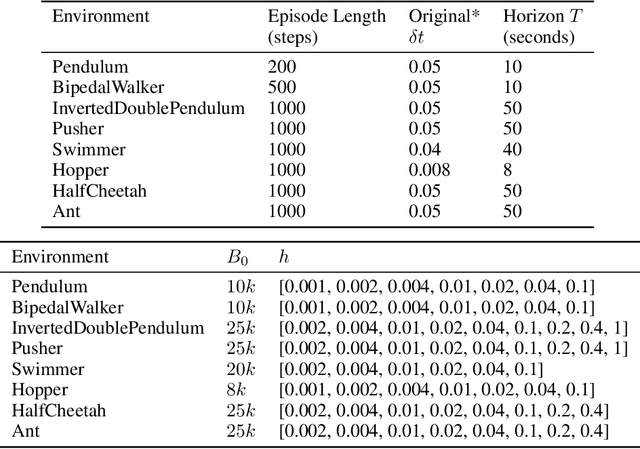
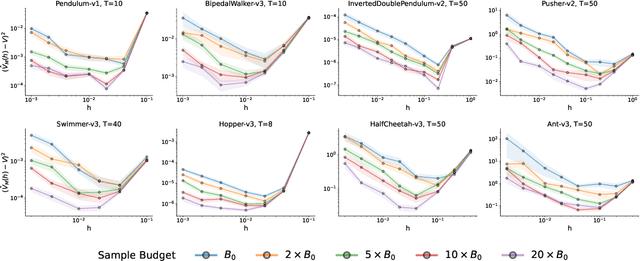
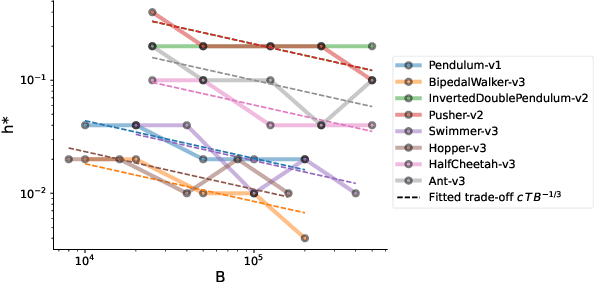
A default assumption in reinforcement learning and optimal control is that experience arrives at discrete time points on a fixed clock cycle. Many applications, however, involve continuous systems where the time discretization is not fixed but instead can be managed by a learning algorithm. By analyzing Monte-Carlo value estimation for LQR systems in both finite-horizon and infinite-horizon settings, we uncover a fundamental trade-off between approximation and statistical error in value estimation. Importantly, these two errors behave differently with respect to time discretization, which implies that there is an optimal choice for the temporal resolution that depends on the data budget. These findings show how adapting the temporal resolution can provably improve value estimation quality in LQR systems from finite data. Empirically, we demonstrate the trade-off in numerical simulations of LQR instances and several non-linear environments.

An Elementary Proof that Q-learning Converges Almost Surely

Watkins' and Dayan's Q-learning is a model-free reinforcement learning algorithm that iteratively refines an estimate for the optimal action-value function of an MDP by stochastically "visiting" many state-ation pairs [Watkins and Dayan, 1992]. Variants of the algorithm lie at the heart of numerous recent state-of-the-art achievements in reinforcement learning, including the superhuman Atari-playing deep Q-network [Mnih et al., 2015]. The goal of this paper is to reproduce a precise and (nearly) self-contained proof that Q-learning converges. Much of the available literature leverages powerful theory to obtain highly generalizable results in this vein. However, this approach requires the reader to be familiar with and make many deep connections to different research areas. A student seeking to deepen their understand of Q-learning risks becoming caught in a vicious cycle of "RL-learning Hell". For this reason, we give a complete proof from start to finish using only one external result from the field of stochastic approximation, despite the fact that this minimal dependence on other results comes at the expense of some "shininess".

Randomized Exploration for Reinforcement Learning with General Value Function Approximation

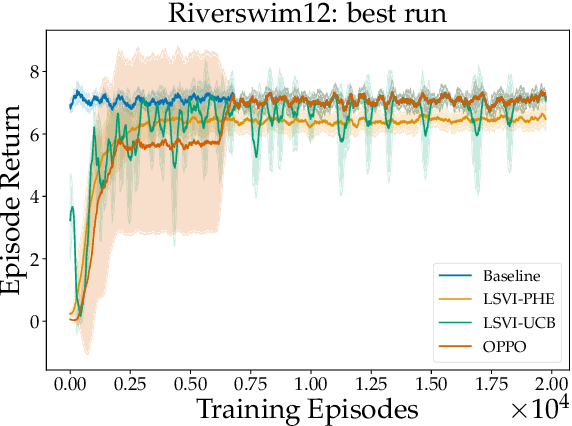
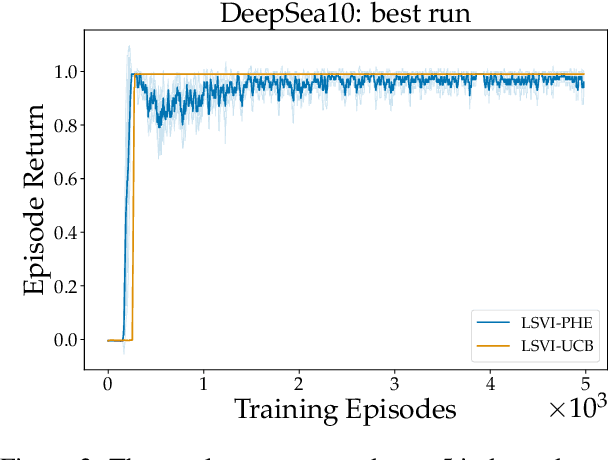
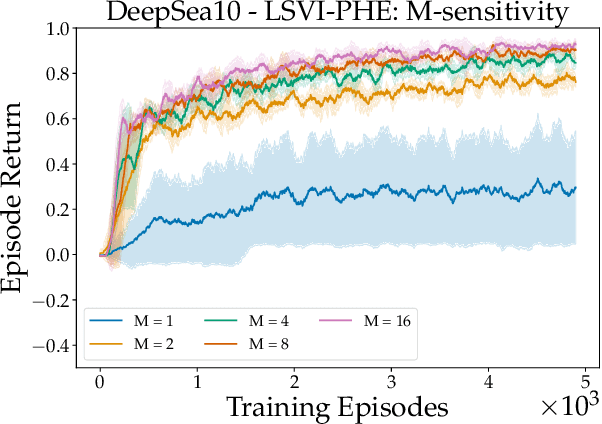
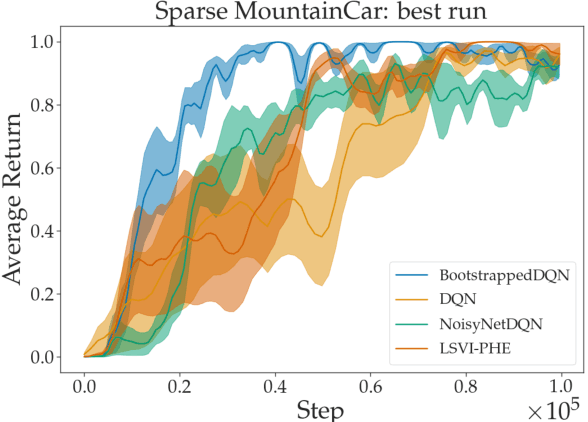
We propose a model-free reinforcement learning algorithm inspired by the popular randomized least squares value iteration (RLSVI) algorithm as well as the optimism principle. Unlike existing upper-confidence-bound (UCB) based approaches, which are often computationally intractable, our algorithm drives exploration by simply perturbing the training data with judiciously chosen i.i.d. scalar noises. To attain optimistic value function estimation without resorting to a UCB-style bonus, we introduce an optimistic reward sampling procedure. When the value functions can be represented by a function class $\mathcal{F}$, our algorithm achieves a worst-case regret bound of $\widetilde{O}(\mathrm{poly}(d_EH)\sqrt{T})$ where $T$ is the time elapsed, $H$ is the planning horizon and $d_E$ is the $\textit{eluder dimension}$ of $\mathcal{F}$. In the linear setting, our algorithm reduces to LSVI-PHE, a variant of RLSVI, that enjoys an $\widetilde{\mathcal{O}}(\sqrt{d^3H^3T})$ regret. We complement the theory with an empirical evaluation across known difficult exploration tasks.

Model-Based Reinforcement Learning with Value-Targeted Regression

This paper studies model-based reinforcement learning (RL) for regret minimization. We focus on finite-horizon episodic RL where the transition model $P$ belongs to a known family of models $\mathcal{P}$, a special case of which is when models in $\mathcal{P}$ take the form of linear mixtures: $P_{\theta} = \sum_{i=1}^{d} \theta_{i}P_{i}$. We propose a model based RL algorithm that is based on optimism principle: In each episode, the set of models that are `consistent' with the data collected is constructed. The criterion of consistency is based on the total squared error of that the model incurs on the task of predicting \emph{values} as determined by the last value estimate along the transitions. The next value function is then chosen by solving the optimistic planning problem with the constructed set of models. We derive a bound on the regret, which, in the special case of linear mixtures, the regret bound takes the form $\tilde{\mathcal{O}}(d\sqrt{H^{3}T})$, where $H$, $T$ and $d$ are the horizon, total number of steps and dimension of $\theta$, respectively. In particular, this regret bound is independent of the total number of states or actions, and is close to a lower bound $\Omega(\sqrt{HdT})$. For a general model family $\mathcal{P}$, the regret bound is derived using the notion of the so-called Eluder dimension proposed by Russo & Van Roy (2014).