Exploration via linearly perturbed loss minimisation
Paper and Code
Nov 13, 2023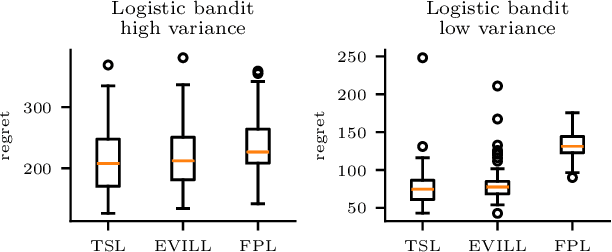
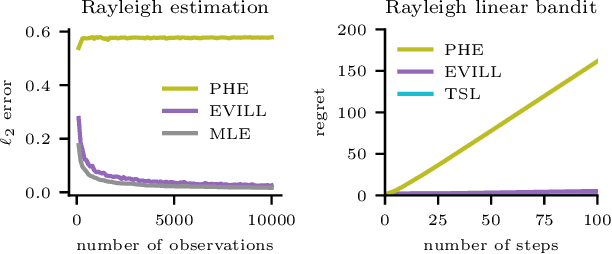
We introduce exploration via linear loss perturbations (EVILL), a randomised exploration method for structured stochastic bandit problems that works by solving for the minimiser of a linearly perturbed regularised negative log-likelihood function. We show that, for the case of generalised linear bandits, EVILL reduces to perturbed history exploration (PHE), a method where exploration is done by training on randomly perturbed rewards. In doing so, we provide a simple and clean explanation of when and why random reward perturbations give rise to good bandit algorithms. With the data-dependent perturbations we propose, not present in previous PHE-type methods, EVILL is shown to match the performance of Thompson-sampling-style parameter-perturbation methods, both in theory and in practice. Moreover, we show an example outside of generalised linear bandits where PHE leads to inconsistent estimates, and thus linear regret, while EVILL remains performant. Like PHE, EVILL can be implemented in just a few lines of code.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge