David Janz
Eluder dimension: localise it!
Jan 14, 2026Abstract:We establish a lower bound on the eluder dimension of generalised linear model classes, showing that standard eluder dimension-based analysis cannot lead to first-order regret bounds. To address this, we introduce a localisation method for the eluder dimension; our analysis immediately recovers and improves on classic results for Bernoulli bandits, and allows for the first genuine first-order bounds for finite-horizon reinforcement learning tasks with bounded cumulative returns.
When and why randomised exploration works (in linear bandits)
Feb 13, 2025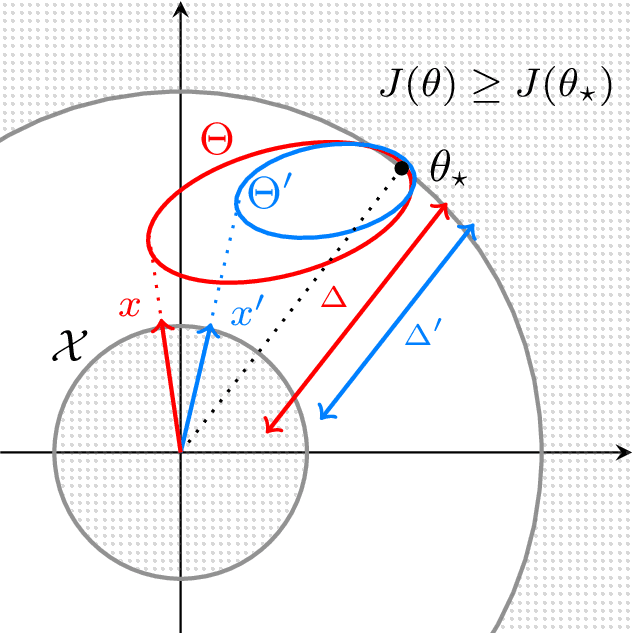
Abstract:We provide an approach for the analysis of randomised exploration algorithms like Thompson sampling that does not rely on forced optimism or posterior inflation. With this, we demonstrate that in the $d$-dimensional linear bandit setting, when the action space is smooth and strongly convex, randomised exploration algorithms enjoy an $n$-step regret bound of the order $O(d\sqrt{n} \log(n))$. Notably, this shows for the first time that there exist non-trivial linear bandit settings where Thompson sampling can achieve optimal dimension dependence in the regret.
Ensemble sampling for linear bandits: small ensembles suffice
Nov 14, 2023Abstract:We provide the first useful, rigorous analysis of ensemble sampling for the stochastic linear bandit setting. In particular, we show that, under standard assumptions, for a $d$-dimensional stochastic linear bandit with an interaction horizon $T$, ensemble sampling with an ensemble of size $m$ on the order of $d \log T$ incurs regret bounded by order $(d \log T)^{5/2} \sqrt{T}$. Ours is the first result in any structured setting not to require the size of the ensemble to scale linearly with $T$ -- which defeats the purpose of ensemble sampling -- while obtaining near $\sqrt{T}$ order regret. Ours is also the first result that allows infinite action sets.
Exploration via linearly perturbed loss minimisation
Nov 13, 2023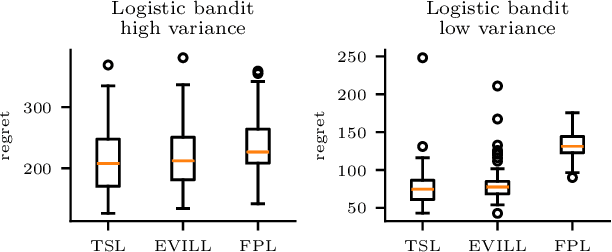
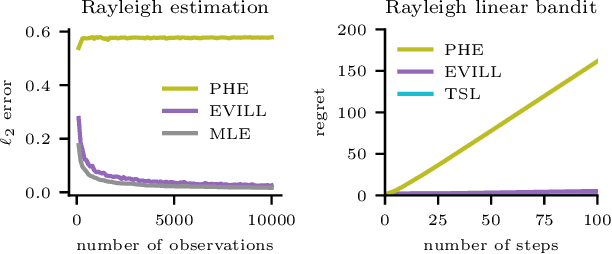
Abstract:We introduce exploration via linear loss perturbations (EVILL), a randomised exploration method for structured stochastic bandit problems that works by solving for the minimiser of a linearly perturbed regularised negative log-likelihood function. We show that, for the case of generalised linear bandits, EVILL reduces to perturbed history exploration (PHE), a method where exploration is done by training on randomly perturbed rewards. In doing so, we provide a simple and clean explanation of when and why random reward perturbations give rise to good bandit algorithms. With the data-dependent perturbations we propose, not present in previous PHE-type methods, EVILL is shown to match the performance of Thompson-sampling-style parameter-perturbation methods, both in theory and in practice. Moreover, we show an example outside of generalised linear bandits where PHE leads to inconsistent estimates, and thus linear regret, while EVILL remains performant. Like PHE, EVILL can be implemented in just a few lines of code.
Stochastic Gradient Descent for Gaussian Processes Done Right
Oct 31, 2023



Abstract:We study the optimisation problem associated with Gaussian process regression using squared loss. The most common approach to this problem is to apply an exact solver, such as conjugate gradient descent, either directly, or to a reduced-order version of the problem. Recently, driven by successes in deep learning, stochastic gradient descent has gained traction as an alternative. In this paper, we show that when done right$\unicode{x2014}$by which we mean using specific insights from the optimisation and kernel communities$\unicode{x2014}$this approach is highly effective. We thus introduce a particular stochastic dual gradient descent algorithm, that may be implemented with a few lines of code using any deep learning framework. We explain our design decisions by illustrating their advantage against alternatives with ablation studies and show that the new method is highly competitive. Our evaluations on standard regression benchmarks and a Bayesian optimisation task set our approach apart from preconditioned conjugate gradients, variational Gaussian process approximations, and a previous version of stochastic gradient descent for Gaussian processes. On a molecular binding affinity prediction task, our method places Gaussian process regression on par in terms of performance with state-of-the-art graph neural networks.
Sampling from Gaussian Process Posteriors using Stochastic Gradient Descent
Jun 20, 2023Abstract:Gaussian processes are a powerful framework for quantifying uncertainty and for sequential decision-making but are limited by the requirement of solving linear systems. In general, this has a cubic cost in dataset size and is sensitive to conditioning. We explore stochastic gradient algorithms as a computationally efficient method of approximately solving these linear systems: we develop low-variance optimization objectives for sampling from the posterior and extend these to inducing points. Counterintuitively, stochastic gradient descent often produces accurate predictions, even in cases where it does not converge quickly to the optimum. We explain this through a spectral characterization of the implicit bias from non-convergence. We show that stochastic gradient descent produces predictive distributions close to the true posterior both in regions with sufficient data coverage, and in regions sufficiently far away from the data. Experimentally, stochastic gradient descent achieves state-of-the-art performance on sufficiently large-scale or ill-conditioned regression tasks. Its uncertainty estimates match the performance of significantly more expensive baselines on a large-scale Bayesian~optimization~task.
Sampling-based inference for large linear models, with application to linearised Laplace
Oct 10, 2022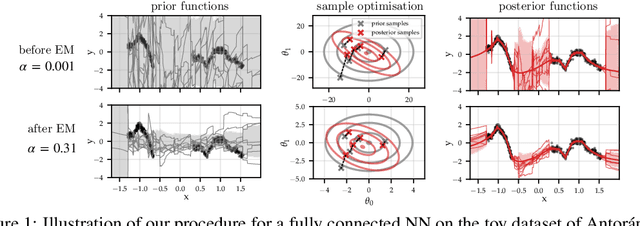
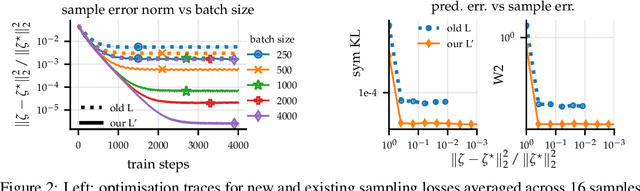

Abstract:Large-scale linear models are ubiquitous throughout machine learning, with contemporary application as surrogate models for neural network uncertainty quantification; that is, the linearised Laplace method. Alas, the computational cost associated with Bayesian linear models constrains this method's application to small networks, small output spaces and small datasets. We address this limitation by introducing a scalable sample-based Bayesian inference method for conjugate Gaussian multi-output linear models, together with a matching method for hyperparameter (regularisation) selection. Furthermore, we use a classic feature normalisation method (the g-prior) to resolve a previously highlighted pathology of the linearised Laplace method. Together, these contributions allow us to perform linearised neural network inference with ResNet-18 on CIFAR100 (11M parameters, 100 output dimensions x 50k datapoints) and with a U-Net on a high-resolution tomographic reconstruction task (2M parameters, 251k output dimensions).
Adapting the Linearised Laplace Model Evidence for Modern Deep Learning
Jun 17, 2022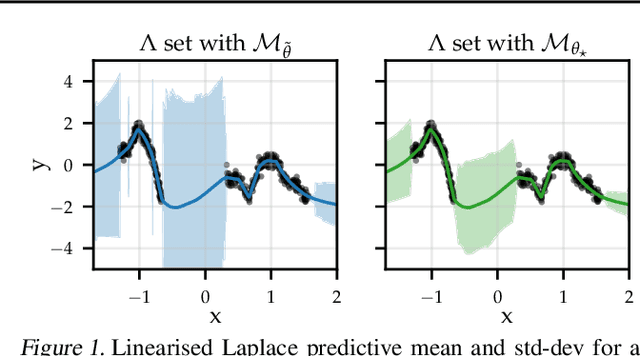

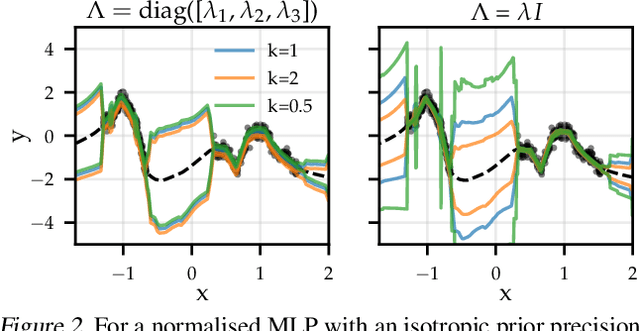

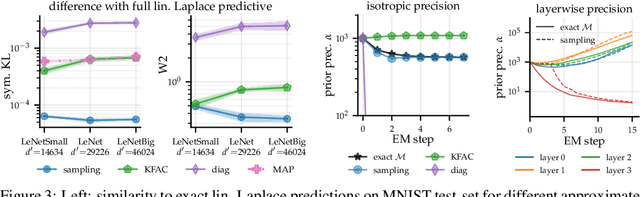
Abstract:The linearised Laplace method for estimating model uncertainty has received renewed attention in the Bayesian deep learning community. The method provides reliable error bars and admits a closed-form expression for the model evidence, allowing for scalable selection of model hyperparameters. In this work, we examine the assumptions behind this method, particularly in conjunction with model selection. We show that these interact poorly with some now-standard tools of deep learning--stochastic approximation methods and normalisation layers--and make recommendations for how to better adapt this classic method to the modern setting. We provide theoretical support for our recommendations and validate them empirically on MLPs, classic CNNs, residual networks with and without normalisation layers, generative autoencoders and transformers.
Bandit optimisation of functions in the Matérn kernel RKHS
Mar 02, 2020

Abstract:We consider the problem of optimising functions in the reproducing kernel Hilbert space (RKHS) of a Mat\'ern kernel with smoothness parameter $\nu$ over the domain $[0,1]^d$ under noisy bandit feedback. Our contribution, the $\pi$-GP-UCB algorithm, is the first practical approach with guaranteed sublinear regret for all $\nu>1$ and $d \geq 1$. Empirical validation suggests better performance and drastically improved computational scalablity compared with its predecessor, Improved GP-UCB.
Learning a Generative Model for Validity in Complex Discrete Structures
Nov 02, 2018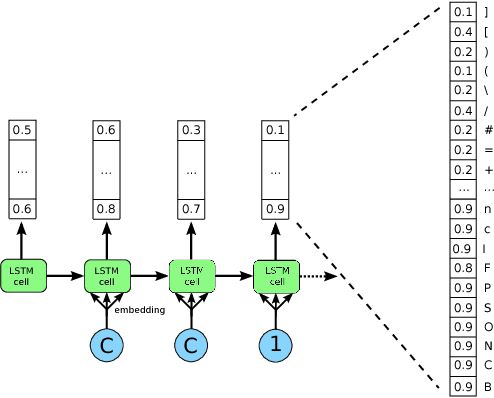
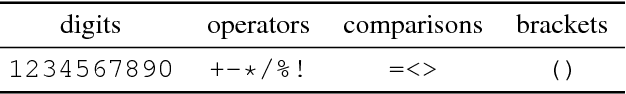
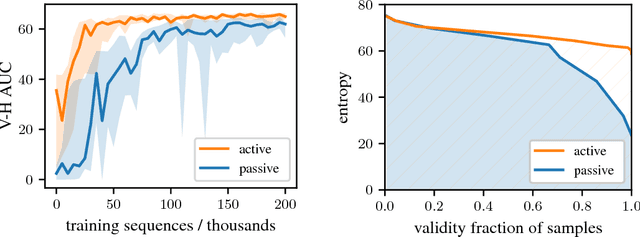

Abstract:Deep generative models have been successfully used to learn representations for high-dimensional discrete spaces by representing discrete objects as sequences and employing powerful sequence-based deep models. Unfortunately, these sequence-based models often produce invalid sequences: sequences which do not represent any underlying discrete structure; invalid sequences hinder the utility of such models. As a step towards solving this problem, we propose to learn a deep recurrent validator model, which can estimate whether a partial sequence can function as the beginning of a full, valid sequence. This validator provides insight as to how individual sequence elements influence the validity of the overall sequence, and can be used to constrain sequence based models to generate valid sequences -- and thus faithfully model discrete objects. Our approach is inspired by reinforcement learning, where an oracle which can evaluate validity of complete sequences provides a sparse reward signal. We demonstrate its effectiveness as a generative model of Python 3 source code for mathematical expressions, and in improving the ability of a variational autoencoder trained on SMILES strings to decode valid molecular structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge