Best Practices for Multi-Fidelity Bayesian Optimization in Materials and Molecular Research

Multi-fidelity Bayesian Optimization (MFBO) is a promising framework to speed up materials and molecular discovery as sources of information of different accuracies are at hand at increasing cost. Despite its potential use in chemical tasks, there is a lack of systematic evaluation of the many parameters playing a role in MFBO. In this work, we provide guidelines and recommendations to decide when to use MFBO in experimental settings. We investigate MFBO methods applied to molecules and materials problems. First, we test two different families of acquisition functions in two synthetic problems and study the effect of the informativeness and cost of the approximate function. We use our implementation and guidelines to benchmark three real discovery problems and compare them against their single-fidelity counterparts. Our results may help guide future efforts to implement MFBO as a routine tool in the chemical sciences.

DEFT: Efficient Finetuning of Conditional Diffusion Models by Learning the Generalised $h$-transform

Generative modelling paradigms based on denoising diffusion processes have emerged as a leading candidate for conditional sampling in inverse problems. In many real-world applications, we often have access to large, expensively trained unconditional diffusion models, which we aim to exploit for improving conditional sampling. Most recent approaches are motivated heuristically and lack a unifying framework, obscuring connections between them. Further, they often suffer from issues such as being very sensitive to hyperparameters, being expensive to train or needing access to weights hidden behind a closed API. In this work, we unify conditional training and sampling using the mathematically well-understood Doob's h-transform. This new perspective allows us to unify many existing methods under a common umbrella. Under this framework, we propose DEFT (Doob's h-transform Efficient FineTuning), a new approach for conditional generation that simply fine-tunes a very small network to quickly learn the conditional $h$-transform, while keeping the larger unconditional network unchanged. DEFT is much faster than existing baselines while achieving state-of-the-art performance across a variety of linear and non-linear benchmarks. On image reconstruction tasks, we achieve speedups of up to 1.6$\times$, while having the best perceptual quality on natural images and reconstruction performance on medical images.

Steerable Conditional Diffusion for Out-of-Distribution Adaptation in Imaging Inverse Problems

Denoising diffusion models have emerged as the go-to framework for solving inverse problems in imaging. A critical concern regarding these models is their performance on out-of-distribution (OOD) tasks, which remains an under-explored challenge. Realistic reconstructions inconsistent with the measured data can be generated, hallucinating image features that are uniquely present in the training dataset. To simultaneously enforce data-consistency and leverage data-driven priors, we introduce a novel sampling framework called Steerable Conditional Diffusion. This framework adapts the denoising network specifically to the available measured data. Utilising our proposed method, we achieve substantial enhancements in OOD performance across diverse imaging modalities, advancing the robust deployment of denoising diffusion models in real-world applications.

Score-Based Generative Models for PET Image Reconstruction

Score-based generative models have demonstrated highly promising results for medical image reconstruction tasks in magnetic resonance imaging or computed tomography. However, their application to Positron Emission Tomography (PET) is still largely unexplored. PET image reconstruction involves a variety of challenges, including Poisson noise with high variance and a wide dynamic range. To address these challenges, we propose several PET-specific adaptations of score-based generative models. The proposed framework is developed for both 2D and 3D PET. In addition, we provide an extension to guided reconstruction using magnetic resonance images. We validate the approach through extensive 2D and 3D $\textit{in-silico}$ experiments with a model trained on patient-realistic data without lesions, and evaluate on data without lesions as well as out-of-distribution data with lesions. This demonstrates the proposed method's robustness and significant potential for improved PET reconstruction.

SVD-DIP: Overcoming the Overfitting Problem in DIP-based CT Reconstruction

The deep image prior (DIP) is a well-established unsupervised deep learning method for image reconstruction; yet it is far from being flawless. The DIP overfits to noise if not early stopped, or optimized via a regularized objective. We build on the regularized fine-tuning of a pretrained DIP, by adopting a novel strategy that restricts the learning to the adaptation of singular values. The proposed SVD-DIP uses ad hoc convolutional layers whose pretrained parameters are decomposed via the singular value decomposition. Optimizing the DIP then solely consists in the fine-tuning of the singular values, while keeping the left and right singular vectors fixed. We thoroughly validate the proposed method on real-measured $\mu$CT data of a lotus root as well as two medical datasets (LoDoPaB and Mayo). We report significantly improved stability of the DIP optimization, by overcoming the overfitting to noise.

Fast and Painless Image Reconstruction in Deep Image Prior Subspaces

The deep image prior (DIP) is a state-of-the-art unsupervised approach for solving linear inverse problems in imaging. We address two key issues that have held back practical deployment of the DIP: the long computing time needed to train a separate deep network per reconstruction, and the susceptibility to overfitting due to a lack of robust early stopping strategies in the unsupervised setting. To this end, we restrict DIP optimisation to a sparse linear subspace of the full parameter space. We construct the subspace from the principal eigenspace of a set of parameter vectors sampled at equally spaced intervals during DIP pre-training on synthetic task-agnostic data. The low-dimensionality of the resulting subspace reduces DIP's capacity to fit noise and allows the use of fast second order optimisation methods, e.g., natural gradient descent or L-BFGS. Experiments across tomographic tasks of different geometry, ill-posedness and stopping criteria consistently show that second order optimisation in a subspace is Pareto-optimal in terms of optimisation time to reconstruction fidelity trade-off.

Sampling-based inference for large linear models, with application to linearised Laplace

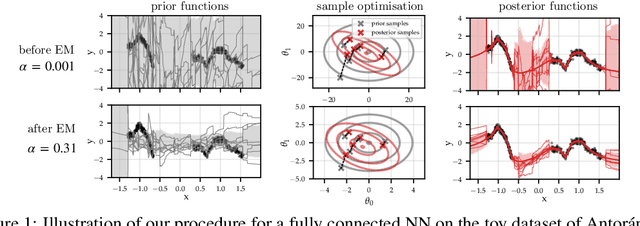
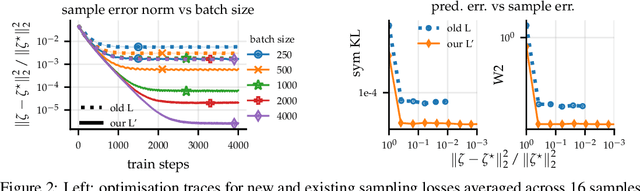
Large-scale linear models are ubiquitous throughout machine learning, with contemporary application as surrogate models for neural network uncertainty quantification; that is, the linearised Laplace method. Alas, the computational cost associated with Bayesian linear models constrains this method's application to small networks, small output spaces and small datasets. We address this limitation by introducing a scalable sample-based Bayesian inference method for conjugate Gaussian multi-output linear models, together with a matching method for hyperparameter (regularisation) selection. Furthermore, we use a classic feature normalisation method (the g-prior) to resolve a previously highlighted pathology of the linearised Laplace method. Together, these contributions allow us to perform linearised neural network inference with ResNet-18 on CIFAR100 (11M parameters, 100 output dimensions x 50k datapoints) and with a U-Net on a high-resolution tomographic reconstruction task (2M parameters, 251k output dimensions).

Bayesian Experimental Design for Computed Tomography with the Linearised Deep Image Prior

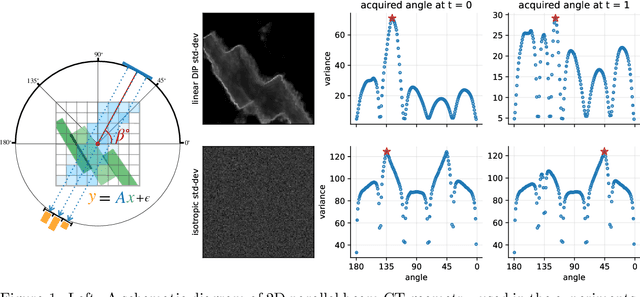
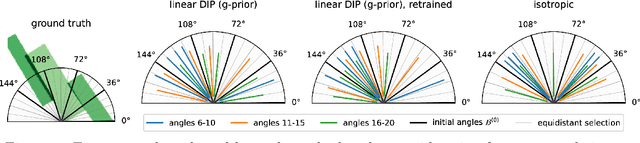
We investigate adaptive design based on a single sparse pilot scan for generating effective scanning strategies for computed tomography reconstruction. We propose a novel approach using the linearised deep image prior. It allows incorporating information from the pilot measurements into the angle selection criteria, while maintaining the tractability of a conjugate Gaussian-linear model. On a synthetically generated dataset with preferential directions, linearised DIP design allows reducing the number of scans by up to 30% relative to an equidistant angle baseline.

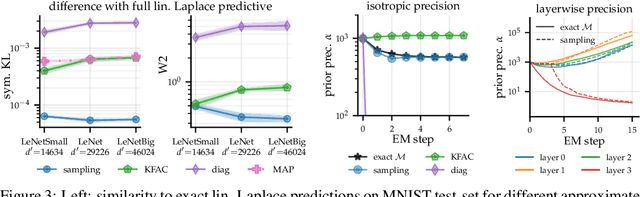
Adapting the Linearised Laplace Model Evidence for Modern Deep Learning

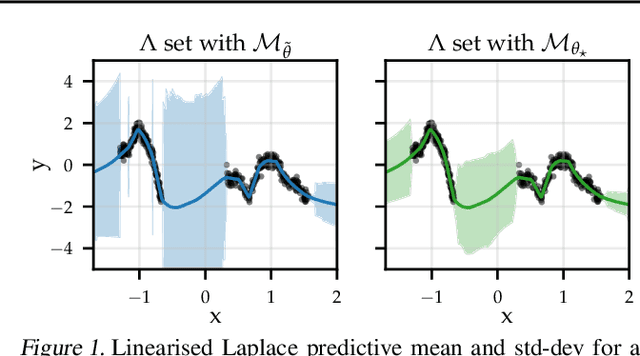
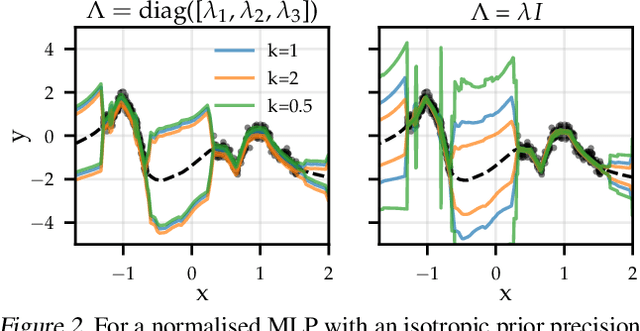
The linearised Laplace method for estimating model uncertainty has received renewed attention in the Bayesian deep learning community. The method provides reliable error bars and admits a closed-form expression for the model evidence, allowing for scalable selection of model hyperparameters. In this work, we examine the assumptions behind this method, particularly in conjunction with model selection. We show that these interact poorly with some now-standard tools of deep learning--stochastic approximation methods and normalisation layers--and make recommendations for how to better adapt this classic method to the modern setting. We provide theoretical support for our recommendations and validate them empirically on MLPs, classic CNNs, residual networks with and without normalisation layers, generative autoencoders and transformers.

A Probabilistic Deep Image Prior for Computational Tomography

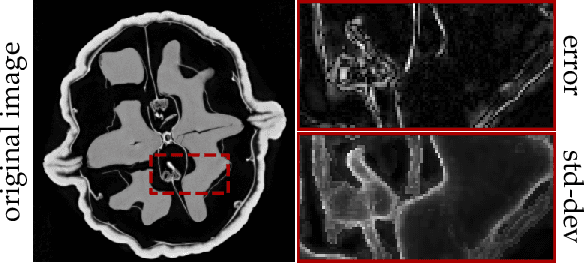
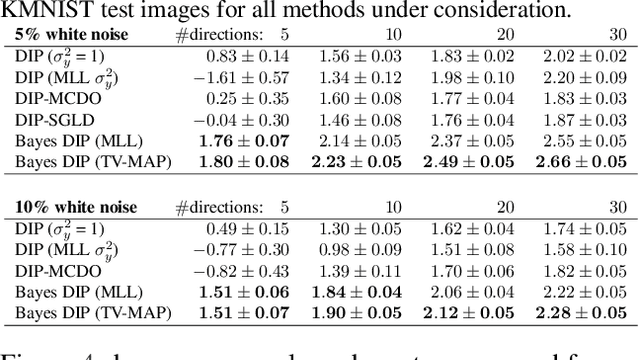
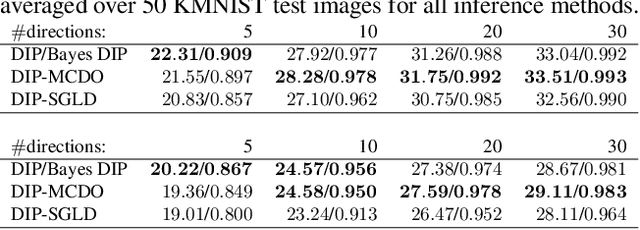
Existing deep-learning based tomographic image reconstruction methods do not provide accurate estimates of reconstruction uncertainty, hindering their real-world deployment. To address this limitation, we construct a Bayesian prior for tomographic reconstruction, which combines the classical total variation (TV) regulariser with the modern deep image prior (DIP). Specifically, we use a change of variables to connect our prior beliefs on the image TV semi-norm with the hyper-parameters of the DIP network. For the inference, we develop an approach based on the linearised Laplace method, which is scalable to high-dimensional settings. The resulting framework provides pixel-wise uncertainty estimates and a marginal likelihood objective for hyperparameter optimisation. We demonstrate the method on synthetic and real-measured high-resolution $\mu$CT data, and show that it provides superior calibration of uncertainty estimates relative to previous probabilistic formulations of the DIP.