Convergence Properties of Score-Based Models using Graduated Optimisation for Linear Inverse Problems

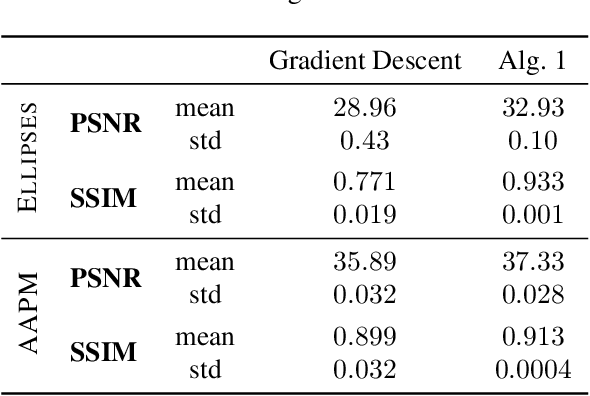
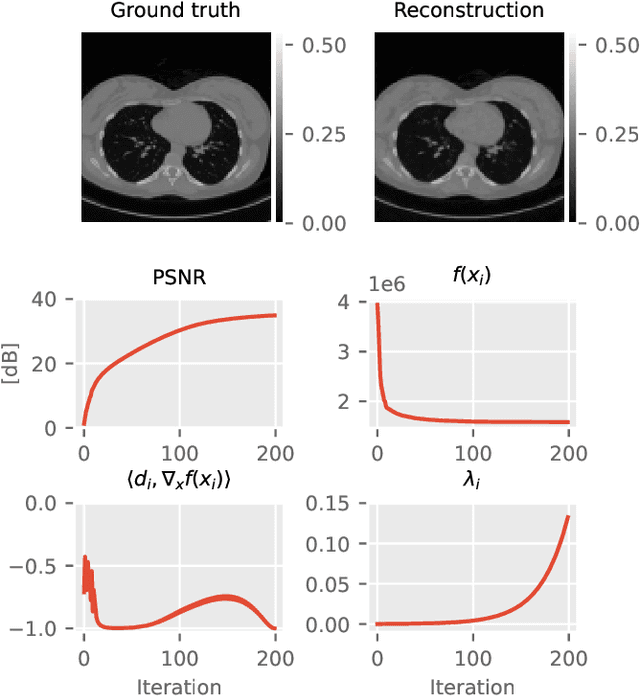
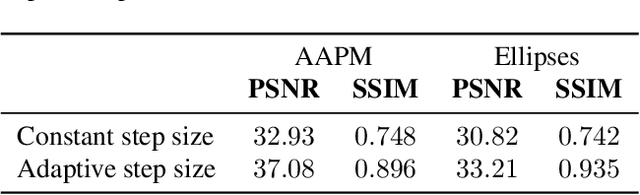
The incorporation of generative models as regularisers within variational formulations for inverse problems has proven effective across numerous image reconstruction tasks. However, the resulting optimisation problem is often non-convex and challenging to solve. In this work, we show that score-based generative models (SGMs) can be used in a graduated optimisation framework to solve inverse problems. We show that the resulting graduated non-convexity flow converge to stationary points of the original problem and provide a numerical convergence analysis of a 2D toy example. We further provide experiments on computed tomography image reconstruction, where we show that this framework is able to recover high-quality images, independent of the initial value. The experiments highlight the potential of using SGMs in graduated optimisation frameworks.

Score-Based Generative Models for PET Image Reconstruction

Score-based generative models have demonstrated highly promising results for medical image reconstruction tasks in magnetic resonance imaging or computed tomography. However, their application to Positron Emission Tomography (PET) is still largely unexplored. PET image reconstruction involves a variety of challenges, including Poisson noise with high variance and a wide dynamic range. To address these challenges, we propose several PET-specific adaptations of score-based generative models. The proposed framework is developed for both 2D and 3D PET. In addition, we provide an extension to guided reconstruction using magnetic resonance images. We validate the approach through extensive 2D and 3D $\textit{in-silico}$ experiments with a model trained on patient-realistic data without lesions, and evaluate on data without lesions as well as out-of-distribution data with lesions. This demonstrates the proposed method's robustness and significant potential for improved PET reconstruction.

Fast and Painless Image Reconstruction in Deep Image Prior Subspaces

The deep image prior (DIP) is a state-of-the-art unsupervised approach for solving linear inverse problems in imaging. We address two key issues that have held back practical deployment of the DIP: the long computing time needed to train a separate deep network per reconstruction, and the susceptibility to overfitting due to a lack of robust early stopping strategies in the unsupervised setting. To this end, we restrict DIP optimisation to a sparse linear subspace of the full parameter space. We construct the subspace from the principal eigenspace of a set of parameter vectors sampled at equally spaced intervals during DIP pre-training on synthetic task-agnostic data. The low-dimensionality of the resulting subspace reduces DIP's capacity to fit noise and allows the use of fast second order optimisation methods, e.g., natural gradient descent or L-BFGS. Experiments across tomographic tasks of different geometry, ill-posedness and stopping criteria consistently show that second order optimisation in a subspace is Pareto-optimal in terms of optimisation time to reconstruction fidelity trade-off.

Quantifying Sources of Uncertainty in Deep Learning-Based Image Reconstruction

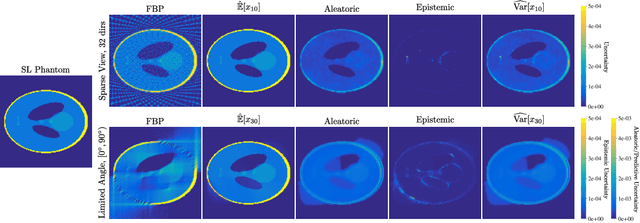
Image reconstruction methods based on deep neural networks have shown outstanding performance, equalling or exceeding the state-of-the-art results of conventional approaches, but often do not provide uncertainty information about the reconstruction. In this work we propose a scalable and efficient framework to simultaneously quantify aleatoric and epistemic uncertainties in learned iterative image reconstruction. We build on a Bayesian deep gradient descent method for quantifying epistemic uncertainty, and incorporate the heteroscedastic variance of the noise to account for the aleatoric uncertainty. We show that our method exhibits competitive performance against conventional benchmarks for computed tomography with both sparse view and limited angle data. The estimated uncertainty captures the variability in the reconstructions, caused by the restricted measurement model, and by missing information, due to the limited angle geometry.