Efficient and Unbiased Sampling of Boltzmann Distributions via Consistency Models

Diffusion models have shown promising potential for advancing Boltzmann Generators. However, two critical challenges persist: (1) inherent errors in samples due to model imperfections, and (2) the requirement of hundreds of functional evaluations (NFEs) to achieve high-quality samples. While existing solutions like importance sampling and distillation address these issues separately, they are often incompatible, as most distillation models lack the necessary density information for importance sampling. This paper introduces a novel sampling method that effectively combines Consistency Models (CMs) with importance sampling. We evaluate our approach on both synthetic energy functions and equivariant n-body particle systems. Our method produces unbiased samples using only 6-25 NFEs while achieving a comparable Effective Sample Size (ESS) to Denoising Diffusion Probabilistic Models (DDPMs) that require approximately 100 NFEs.

Improving Linear System Solvers for Hyperparameter Optimisation in Iterative Gaussian Processes

Scaling hyperparameter optimisation to very large datasets remains an open problem in the Gaussian process community. This paper focuses on iterative methods, which use linear system solvers, like conjugate gradients, alternating projections or stochastic gradient descent, to construct an estimate of the marginal likelihood gradient. We discuss three key improvements which are applicable across solvers: (i) a pathwise gradient estimator, which reduces the required number of solver iterations and amortises the computational cost of making predictions, (ii) warm starting linear system solvers with the solution from the previous step, which leads to faster solver convergence at the cost of negligible bias, (iii) early stopping linear system solvers after a limited computational budget, which synergises with warm starting, allowing solver progress to accumulate over multiple marginal likelihood steps. These techniques provide speed-ups of up to $72\times$ when solving to tolerance, and decrease the average residual norm by up to $7\times$ when stopping early.

A Generative Model of Symmetry Transformations

Correctly capturing the symmetry transformations of data can lead to efficient models with strong generalization capabilities, though methods incorporating symmetries often require prior knowledge. While recent advancements have been made in learning those symmetries directly from the dataset, most of this work has focused on the discriminative setting. In this paper, we construct a generative model that explicitly aims to capture symmetries in the data, resulting in a model that learns which symmetries are present in an interpretable way. We provide a simple algorithm for efficiently learning our generative model and demonstrate its ability to capture symmetries under affine and color transformations. Combining our symmetry model with existing generative models results in higher marginal test-log-likelihoods and robustness to data sparsification.

Stochastic Gradient Descent for Gaussian Processes Done Right

We study the optimisation problem associated with Gaussian process regression using squared loss. The most common approach to this problem is to apply an exact solver, such as conjugate gradient descent, either directly, or to a reduced-order version of the problem. Recently, driven by successes in deep learning, stochastic gradient descent has gained traction as an alternative. In this paper, we show that when done right$\unicode{x2014}$by which we mean using specific insights from the optimisation and kernel communities$\unicode{x2014}$this approach is highly effective. We thus introduce a particular stochastic dual gradient descent algorithm, that may be implemented with a few lines of code using any deep learning framework. We explain our design decisions by illustrating their advantage against alternatives with ablation studies and show that the new method is highly competitive. Our evaluations on standard regression benchmarks and a Bayesian optimisation task set our approach apart from preconditioned conjugate gradients, variational Gaussian process approximations, and a previous version of stochastic gradient descent for Gaussian processes. On a molecular binding affinity prediction task, our method places Gaussian process regression on par in terms of performance with state-of-the-art graph neural networks.

SE(3) Equivariant Augmented Coupling Flows

Coupling normalizing flows allow for fast sampling and density evaluation, making them the tool of choice for probabilistic modeling of physical systems. However, the standard coupling architecture precludes endowing flows that operate on the Cartesian coordinates of atoms with the SE(3) and permutation invariances of physical systems. This work proposes a coupling flow that preserves SE(3) and permutation equivariance by performing coordinate splits along additional augmented dimensions. At each layer, the flow maps atoms' positions into learned SE(3) invariant bases, where we apply standard flow transformations, such as monotonic rational-quadratic splines, before returning to the original basis. Crucially, our flow preserves fast sampling and density evaluation, and may be used to produce unbiased estimates of expectations with respect to the target distribution via importance sampling. When trained on the DW4, LJ13 and QM9-positional datasets, our flow is competitive with equivariant continuous normalizing flows, while allowing sampling two orders of magnitude faster. Moreover, to the best of our knowledge, we are the first to learn the full Boltzmann distribution of alanine dipeptide by only modeling the Cartesian positions of its atoms. Lastly, we demonstrate that our flow can be trained to approximately sample from the Boltzmann distribution of the DW4 and LJ13 particle systems using only their energy functions.

Online Laplace Model Selection Revisited

The Laplace approximation provides a closed-form model selection objective for neural networks (NN). Online variants, which optimise NN parameters jointly with hyperparameters, like weight decay strength, have seen renewed interest in the Bayesian deep learning community. However, these methods violate Laplace's method's critical assumption that the approximation is performed around a mode of the loss, calling into question their soundness. This work re-derives online Laplace methods, showing them to target a variational bound on a mode-corrected variant of the Laplace evidence which does not make stationarity assumptions. Online Laplace and its mode-corrected counterpart share stationary points where 1. the NN parameters are a maximum a posteriori, satisfying the Laplace method's assumption, and 2. the hyperparameters maximise the Laplace evidence, motivating online methods. We demonstrate that these optima are roughly attained in practise by online algorithms using full-batch gradient descent on UCI regression datasets. The optimised hyperparameters prevent overfitting and outperform validation-based early stopping.

Sampling from Gaussian Process Posteriors using Stochastic Gradient Descent

Gaussian processes are a powerful framework for quantifying uncertainty and for sequential decision-making but are limited by the requirement of solving linear systems. In general, this has a cubic cost in dataset size and is sensitive to conditioning. We explore stochastic gradient algorithms as a computationally efficient method of approximately solving these linear systems: we develop low-variance optimization objectives for sampling from the posterior and extend these to inducing points. Counterintuitively, stochastic gradient descent often produces accurate predictions, even in cases where it does not converge quickly to the optimum. We explain this through a spectral characterization of the implicit bias from non-convergence. We show that stochastic gradient descent produces predictive distributions close to the true posterior both in regions with sufficient data coverage, and in regions sufficiently far away from the data. Experimentally, stochastic gradient descent achieves state-of-the-art performance on sufficiently large-scale or ill-conditioned regression tasks. Its uncertainty estimates match the performance of significantly more expensive baselines on a large-scale Bayesian~optimization~task.

Fast and Painless Image Reconstruction in Deep Image Prior Subspaces

The deep image prior (DIP) is a state-of-the-art unsupervised approach for solving linear inverse problems in imaging. We address two key issues that have held back practical deployment of the DIP: the long computing time needed to train a separate deep network per reconstruction, and the susceptibility to overfitting due to a lack of robust early stopping strategies in the unsupervised setting. To this end, we restrict DIP optimisation to a sparse linear subspace of the full parameter space. We construct the subspace from the principal eigenspace of a set of parameter vectors sampled at equally spaced intervals during DIP pre-training on synthetic task-agnostic data. The low-dimensionality of the resulting subspace reduces DIP's capacity to fit noise and allows the use of fast second order optimisation methods, e.g., natural gradient descent or L-BFGS. Experiments across tomographic tasks of different geometry, ill-posedness and stopping criteria consistently show that second order optimisation in a subspace is Pareto-optimal in terms of optimisation time to reconstruction fidelity trade-off.

Sampling-based inference for large linear models, with application to linearised Laplace

Large-scale linear models are ubiquitous throughout machine learning, with contemporary application as surrogate models for neural network uncertainty quantification; that is, the linearised Laplace method. Alas, the computational cost associated with Bayesian linear models constrains this method's application to small networks, small output spaces and small datasets. We address this limitation by introducing a scalable sample-based Bayesian inference method for conjugate Gaussian multi-output linear models, together with a matching method for hyperparameter (regularisation) selection. Furthermore, we use a classic feature normalisation method (the g-prior) to resolve a previously highlighted pathology of the linearised Laplace method. Together, these contributions allow us to perform linearised neural network inference with ResNet-18 on CIFAR100 (11M parameters, 100 output dimensions x 50k datapoints) and with a U-Net on a high-resolution tomographic reconstruction task (2M parameters, 251k output dimensions).

Bayesian Experimental Design for Computed Tomography with the Linearised Deep Image Prior

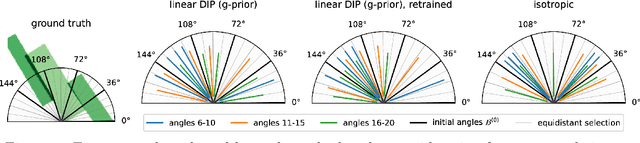
We investigate adaptive design based on a single sparse pilot scan for generating effective scanning strategies for computed tomography reconstruction. We propose a novel approach using the linearised deep image prior. It allows incorporating information from the pilot measurements into the angle selection criteria, while maintaining the tractability of a conjugate Gaussian-linear model. On a synthetically generated dataset with preferential directions, linearised DIP design allows reducing the number of scans by up to 30% relative to an equidistant angle baseline.