SE(3) Equivariant Augmented Coupling Flows

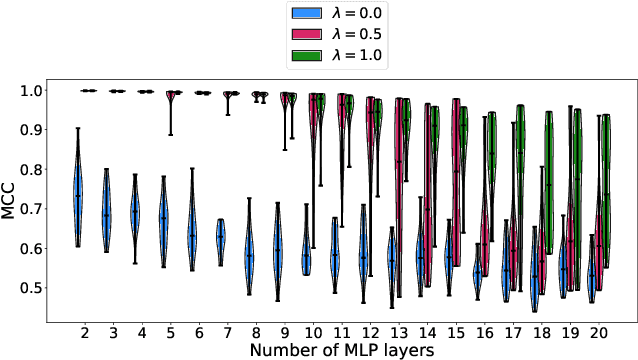
Coupling normalizing flows allow for fast sampling and density evaluation, making them the tool of choice for probabilistic modeling of physical systems. However, the standard coupling architecture precludes endowing flows that operate on the Cartesian coordinates of atoms with the SE(3) and permutation invariances of physical systems. This work proposes a coupling flow that preserves SE(3) and permutation equivariance by performing coordinate splits along additional augmented dimensions. At each layer, the flow maps atoms' positions into learned SE(3) invariant bases, where we apply standard flow transformations, such as monotonic rational-quadratic splines, before returning to the original basis. Crucially, our flow preserves fast sampling and density evaluation, and may be used to produce unbiased estimates of expectations with respect to the target distribution via importance sampling. When trained on the DW4, LJ13 and QM9-positional datasets, our flow is competitive with equivariant continuous normalizing flows, while allowing sampling two orders of magnitude faster. Moreover, to the best of our knowledge, we are the first to learn the full Boltzmann distribution of alanine dipeptide by only modeling the Cartesian positions of its atoms. Lastly, we demonstrate that our flow can be trained to approximately sample from the Boltzmann distribution of the DW4 and LJ13 particle systems using only their energy functions.

Flow Annealed Importance Sampling Bootstrap

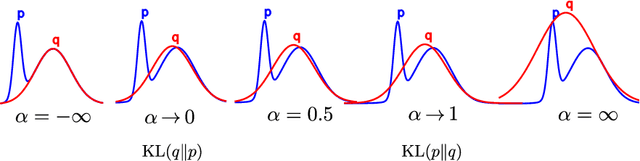
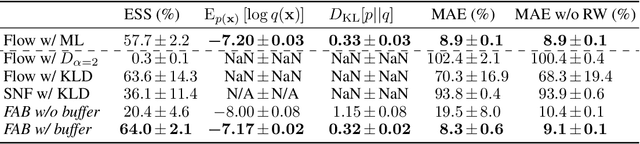
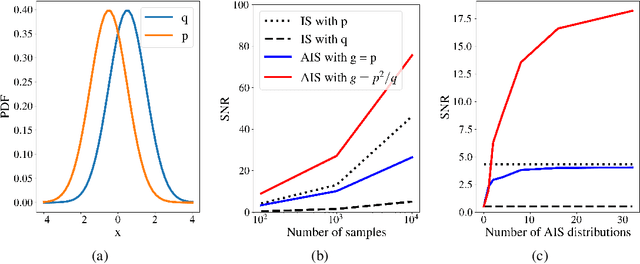
Normalizing flows are tractable density models that can approximate complicated target distributions, e.g. Boltzmann distributions of physical systems. However, current methods for training flows either suffer from mode-seeking behavior, use samples from the target generated beforehand by expensive MCMC simulations, or use stochastic losses that have very high variance. To avoid these problems, we augment flows with annealed importance sampling (AIS) and minimize the mass covering $\alpha$-divergence with $\alpha=2$, which minimizes importance weight variance. Our method, Flow AIS Bootstrap (FAB), uses AIS to generate samples in regions where the flow is a poor approximation of the target, facilitating the discovery of new modes. We target with AIS the minimum variance distribution for the estimation of the $\alpha$-divergence via importance sampling. We also use a prioritized buffer to store and reuse AIS samples. These two features significantly improve FAB's performance. We apply FAB to complex multimodal targets and show that we can approximate them very accurately where previous methods fail. To the best of our knowledge, we are the first to learn the Boltzmann distribution of the alanine dipeptide molecule using only the unnormalized target density and without access to samples generated via Molecular Dynamics (MD) simulations: FAB produces better results than training via maximum likelihood on MD samples while using 100 times fewer target evaluations. After reweighting samples with importance weights, we obtain unbiased histograms of dihedral angles that are almost identical to the ground truth ones.

Probing the Robustness of Independent Mechanism Analysis for Representation Learning

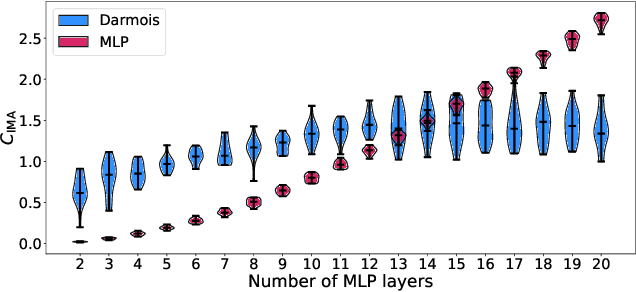
One aim of representation learning is to recover the original latent code that generated the data, a task which requires additional information or inductive biases. A recently proposed approach termed Independent Mechanism Analysis (IMA) postulates that each latent source should influence the observed mixtures independently, complementing standard nonlinear independent component analysis, and taking inspiration from the principle of independent causal mechanisms. While it was shown in theory and experiments that IMA helps recovering the true latents, the method's performance was so far only characterized when the modeling assumptions are exactly satisfied. Here, we test the method's robustness to violations of the underlying assumptions. We find that the benefits of IMA-based regularization for recovering the true sources extend to mixing functions with various degrees of violation of the IMA principle, while standard regularizers do not provide the same merits. Moreover, we show that unregularized maximum likelihood recovers mixing functions which systematically deviate from the IMA principle, and provide an argument elucidating the benefits of IMA-based regularization.

AutoML Two-Sample Test

Two-sample tests are important in statistics and machine learning, both as tools for scientific discovery as well as to detect distribution shifts. This led to the development of many sophisticated test procedures going beyond the standard supervised learning frameworks, whose usage can require specialized knowledge about two-sample testing. We use a simple test that takes the mean discrepancy of a witness function as the test statistic and prove that minimizing a squared loss leads to a witness with optimal testing power. This allows us to leverage recent advancements in AutoML. Without any user input about the problems at hand, and using the same method for all our experiments, our AutoML two-sample test achieves competitive performance on a diverse distribution shift benchmark as well as on challenging two-sample testing problems. We provide an implementation of the AutoML two-sample test in the Python package autotst.

Bootstrap Your Flow

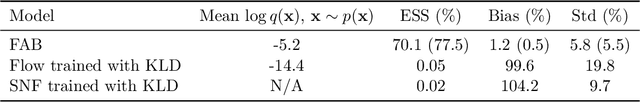
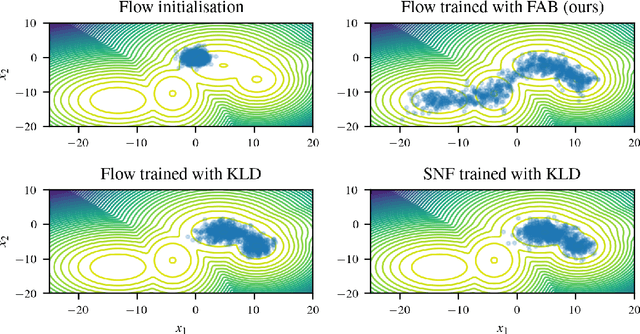
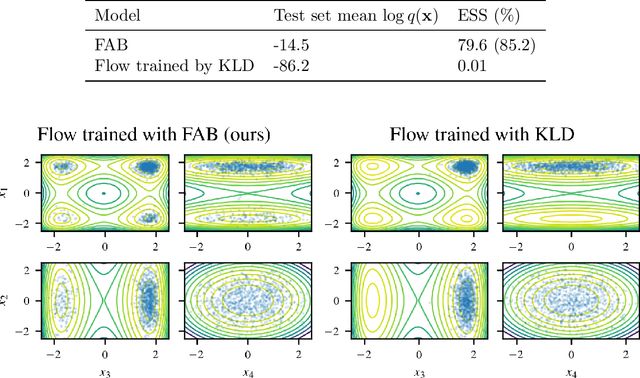
Normalising flows are flexible, parameterized distributions that can be used to approximate expectations from intractable distributions via importance sampling. However, current flow-based approaches are limited on challenging targets where they either suffer from mode seeking behaviour or high variance in the training loss, or rely on samples from the target distribution, which may not be available. To address these challenges, we combine flows with annealed importance sampling (AIS), while using the $\alpha$-divergence as our objective, in a novel training procedure, FAB (Flow AIS Bootstrap). Thereby, the flow and AIS to improve each other in a bootstrapping manner. We demonstrate that FAB can be used to produce accurate approximations to complex target distributions, including Boltzmann distributions, in problems where previous flow-based methods fail.

Resampling Base Distributions of Normalizing Flows

Normalizing flows are a popular class of models for approximating probability distributions. However, their invertible nature limits their ability to model target distributions with a complex topological structure, such as Boltzmann distributions. Several procedures have been proposed to solve this problem but many of them sacrifice invertibility and, thereby, tractability of the log-likelihood as well as other desirable properties. To address these limitations, we introduce a base distribution for normalizing flows based on learned rejection sampling, allowing the resulting normalizing flow to model complex topologies without giving up bijectivity. Furthermore, we develop suitable learning algorithms using both maximizing the log-likelihood and the optimization of the reverse Kullback-Leibler divergence, and apply them to various sample problems, i.e.\ approximating 2D densities, density estimation of tabular data, image generation, and modeling Boltzmann distributions. In these experiments our method is competitive with or outperforms the baselines.

Independent mechanism analysis, a new concept?

Independent component analysis provides a principled framework for unsupervised representation learning, with solid theory on the identifiability of the latent code that generated the data, given only observations of mixtures thereof. Unfortunately, when the mixing is nonlinear, the model is provably nonidentifiable, since statistical independence alone does not sufficiently constrain the problem. Identifiability can be recovered in settings where additional, typically observed variables are included in the generative process. We investigate an alternative path and consider instead including assumptions reflecting the principle of independent causal mechanisms exploited in the field of causality. Specifically, our approach is motivated by thinking of each source as independently influencing the mixing process. This gives rise to a framework which we term independent mechanism analysis. We provide theoretical and empirical evidence that our approach circumvents a number of nonidentifiability issues arising in nonlinear blind source separation.