Independent Mechanism Analysis and the Manifold Hypothesis

Independent Mechanism Analysis (IMA) seeks to address non-identifiability in nonlinear Independent Component Analysis (ICA) by assuming that the Jacobian of the mixing function has orthogonal columns. As typical in ICA, previous work focused on the case with an equal number of latent components and observed mixtures. Here, we extend IMA to settings with a larger number of mixtures that reside on a manifold embedded in a higher-dimensional than the latent space -- in line with the manifold hypothesis in representation learning. For this setting, we show that IMA still circumvents several non-identifiability issues, suggesting that it can also be a beneficial principle for higher-dimensional observations when the manifold hypothesis holds. Further, we prove that the IMA principle is approximately satisfied with high probability (increasing with the number of observed mixtures) when the directions along which the latent components influence the observations are chosen independently at random. This provides a new and rigorous statistical interpretation of IMA.

Probing the Robustness of Independent Mechanism Analysis for Representation Learning

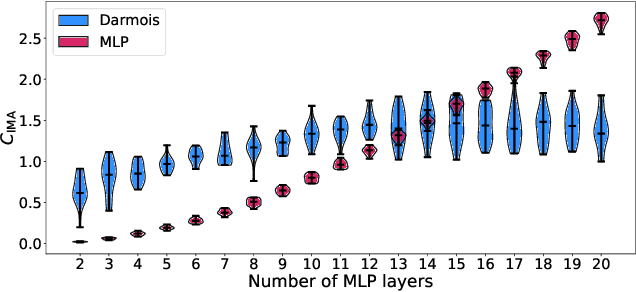
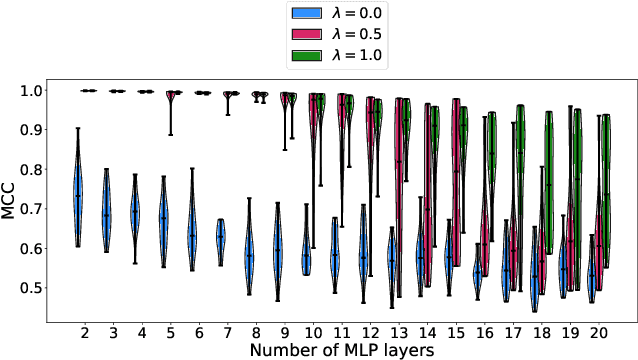
One aim of representation learning is to recover the original latent code that generated the data, a task which requires additional information or inductive biases. A recently proposed approach termed Independent Mechanism Analysis (IMA) postulates that each latent source should influence the observed mixtures independently, complementing standard nonlinear independent component analysis, and taking inspiration from the principle of independent causal mechanisms. While it was shown in theory and experiments that IMA helps recovering the true latents, the method's performance was so far only characterized when the modeling assumptions are exactly satisfied. Here, we test the method's robustness to violations of the underlying assumptions. We find that the benefits of IMA-based regularization for recovering the true sources extend to mixing functions with various degrees of violation of the IMA principle, while standard regularizers do not provide the same merits. Moreover, we show that unregularized maximum likelihood recovers mixing functions which systematically deviate from the IMA principle, and provide an argument elucidating the benefits of IMA-based regularization.

On Pitfalls of Identifiability in Unsupervised Learning. A Note on: "Desiderata for Representation Learning: A Causal Perspective"

Model identifiability is a desirable property in the context of unsupervised representation learning. In absence thereof, different models may be observationally indistinguishable while yielding representations that are nontrivially related to one another, thus making the recovery of a ground truth generative model fundamentally impossible, as often shown through suitably constructed counterexamples. In this note, we discuss one such construction, illustrating a potential failure case of an identifiability result presented in "Desiderata for Representation Learning: A Causal Perspective" by Wang & Jordan (2021). The construction is based on the theory of nonlinear independent component analysis. We comment on implications of this and other counterexamples for identifiable representation learning.