Controlling for discrete unmeasured confounding in nonlinear causal models

Unmeasured confounding is a major challenge for identifying causal relationships from non-experimental data. Here, we propose a method that can accommodate unmeasured discrete confounding. Extending recent identifiability results in deep latent variable models, we show theoretically that confounding can be detected and corrected under the assumption that the observed data is a piecewise affine transformation of a latent Gaussian mixture model and that the identity of the mixture components is confounded. We provide a flow-based algorithm to estimate this model and perform deconfounding. Experimental results on synthetic and real-world data provide support for the effectiveness of our approach.

Independent Mechanism Analysis and the Manifold Hypothesis

Independent Mechanism Analysis (IMA) seeks to address non-identifiability in nonlinear Independent Component Analysis (ICA) by assuming that the Jacobian of the mixing function has orthogonal columns. As typical in ICA, previous work focused on the case with an equal number of latent components and observed mixtures. Here, we extend IMA to settings with a larger number of mixtures that reside on a manifold embedded in a higher-dimensional than the latent space -- in line with the manifold hypothesis in representation learning. For this setting, we show that IMA still circumvents several non-identifiability issues, suggesting that it can also be a beneficial principle for higher-dimensional observations when the manifold hypothesis holds. Further, we prove that the IMA principle is approximately satisfied with high probability (increasing with the number of observed mixtures) when the directions along which the latent components influence the observations are chosen independently at random. This provides a new and rigorous statistical interpretation of IMA.

Targeted Reduction of Causal Models

Why does a phenomenon occur? Addressing this question is central to most scientific inquiries based on empirical observations, and often heavily relies on simulations of scientific models. As models become more intricate, deciphering the causes behind these phenomena in high-dimensional spaces of interconnected variables becomes increasingly challenging. Causal machine learning may assist scientists in the discovery of relevant and interpretable patterns of causation in simulations. We introduce Targeted Causal Reduction (TCR), a method for turning complex models into a concise set of causal factors that explain a specific target phenomenon. We derive an information theoretic objective to learn TCR from interventional data or simulations and propose algorithms to optimize this objective efficiently. TCR's ability to generate interpretable high-level explanations from complex models is demonstrated on toy and mechanical systems, illustrating its potential to assist scientists in the study of complex phenomena in a broad range of disciplines.

Nonparametric Identifiability of Causal Representations from Unknown Interventions

We study causal representation learning, the task of inferring latent causal variables and their causal relations from high-dimensional functions ("mixtures") of the variables. Prior work relies on weak supervision, in the form of counterfactual pre- and post-intervention views or temporal structure; places restrictive assumptions, such as linearity, on the mixing function or latent causal model; or requires partial knowledge of the generative process, such as the causal graph or the intervention targets. We instead consider the general setting in which both the causal model and the mixing function are nonparametric. The learning signal takes the form of multiple datasets, or environments, arising from unknown interventions in the underlying causal model. Our goal is to identify both the ground truth latents and their causal graph up to a set of ambiguities which we show to be irresolvable from interventional data. We study the fundamental setting of two causal variables and prove that the observational distribution and one perfect intervention per node suffice for identifiability, subject to a genericity condition. This condition rules out spurious solutions that involve fine-tuning of the intervened and observational distributions, mirroring similar conditions for nonlinear cause-effect inference. For an arbitrary number of variables, we show that two distinct paired perfect interventions per node guarantee identifiability. Further, we demonstrate that the strengths of causal influences among the latent variables are preserved by all equivalent solutions, rendering the inferred representation appropriate for drawing causal conclusions from new data. Our study provides the first identifiability results for the general nonparametric setting with unknown interventions, and elucidates what is possible and impossible for causal representation learning without more direct supervision.

Causal Component Analysis

Independent Component Analysis (ICA) aims to recover independent latent variables from observed mixtures thereof. Causal Representation Learning (CRL) aims instead to infer causally related (thus often statistically dependent) latent variables, together with the unknown graph encoding their causal relationships. We introduce an intermediate problem termed Causal Component Analysis (CauCA). CauCA can be viewed as a generalization of ICA, modelling the causal dependence among the latent components, and as a special case of CRL. In contrast to CRL, it presupposes knowledge of the causal graph, focusing solely on learning the unmixing function and the causal mechanisms. Any impossibility results regarding the recovery of the ground truth in CauCA also apply for CRL, while possibility results may serve as a stepping stone for extensions to CRL. We characterize CauCA identifiability from multiple datasets generated through different types of interventions on the latent causal variables. As a corollary, this interventional perspective also leads to new identifiability results for nonlinear ICA -- a special case of CauCA with an empty graph -- requiring strictly fewer datasets than previous results. We introduce a likelihood-based approach using normalizing flows to estimate both the unmixing function and the causal mechanisms, and demonstrate its effectiveness through extensive synthetic experiments in the CauCA and ICA setting.

Information Theoretic Measures of Causal Influences during Transient Neural Events

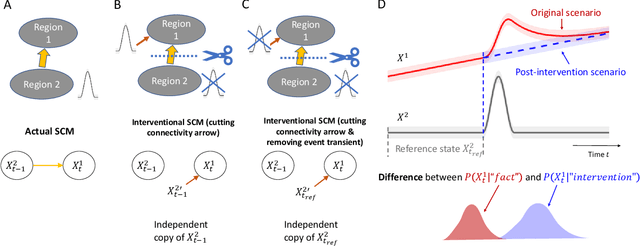
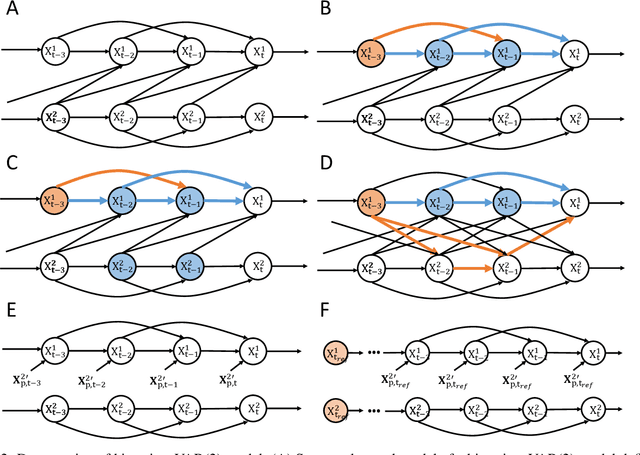
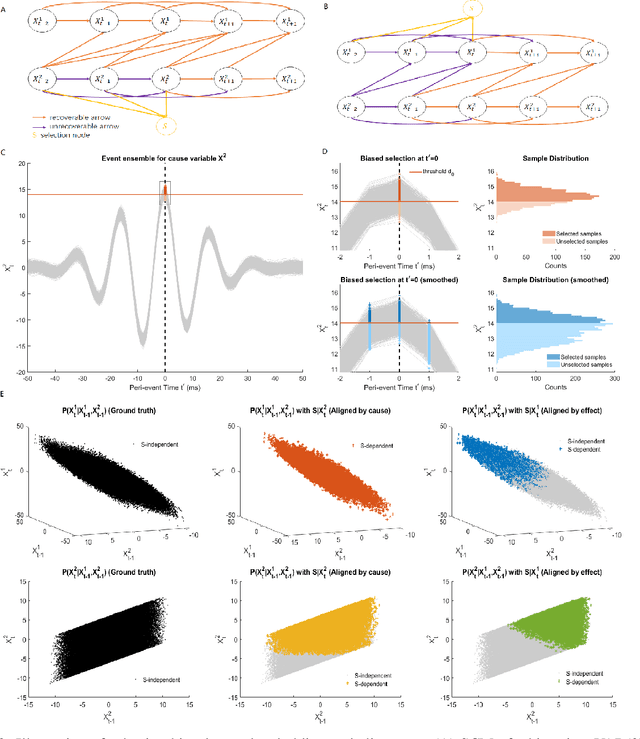
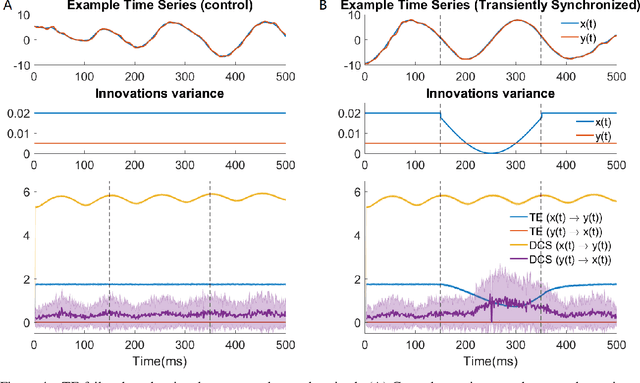
Transient phenomena play a key role in coordinating brain activity at multiple scales, however,their underlying mechanisms remain largely unknown. A key challenge for neural data science is thus to characterize the network interactions at play during these events. Using the formalism of Structural Causal Models and their graphical representation, we investigate the theoretical and empirical properties of Information Theory based causal strength measures in the context of recurring spontaneous transient events. After showing the limitations of Transfer Entropy and Dynamic Causal Strength in such a setting, we introduce a novel measure, relative Dynamic Causal Strength, and provide theoretical and empirical support for its benefits. These methods are applied to simulated and experimentally recorded neural time series, and provide results in agreement with our current understanding of the underlying brain circuits.

Function Classes for Identifiable Nonlinear Independent Component Analysis

Unsupervised learning of latent variable models (LVMs) is widely used to represent data in machine learning. When such models reflect the ground truth factors and the mechanisms mapping them to observations, there is reason to expect that they allow generalization in downstream tasks. It is however well known that such identifiability guaranties are typically not achievable without putting constraints on the model class. This is notably the case for nonlinear Independent Component Analysis, in which the LVM maps statistically independent variables to observations via a deterministic nonlinear function. Several families of spurious solutions fitting perfectly the data, but that do not correspond to the ground truth factors can be constructed in generic settings. However, recent work suggests that constraining the function class of such models may promote identifiability. Specifically, function classes with constraints on their partial derivatives, gathered in the Jacobian matrix, have been proposed, such as orthogonal coordinate transformations (OCT), which impose orthogonality of the Jacobian columns. In the present work, we prove that a subclass of these transformations, conformal maps, is identifiable and provide novel theoretical results suggesting that OCTs have properties that prevent families of spurious solutions to spoil identifiability in a generic setting.

Homomorphism Autoencoder -- Learning Group Structured Representations from Observed Transitions

How can we acquire world models that veridically represent the outside world both in terms of what is there and in terms of how our actions affect it? Can we acquire such models by interacting with the world, and can we state mathematical desiderata for their relationship with a hypothetical reality existing outside our heads? As machine learning is moving towards representations containing not just observational but also interventional knowledge, we study these problems using tools from representation learning and group theory. Under the assumption that our actuators act upon the world, we propose methods to learn internal representations of not just sensory information but also of actions that modify our sensory representations in a way that is consistent with the actions and transitions in the world. We use an autoencoder equipped with a group representation linearly acting on its latent space, trained on 2-step reconstruction such as to enforce a suitable homomorphism property on the group representation. Compared to existing work, our approach makes fewer assumptions on the group representation and on which transformations the agent can sample from the group. We motivate our method theoretically, and demonstrate empirically that it can learn the correct representation of the groups and the topology of the environment. We also compare its performance in trajectory prediction with previous methods.

Embrace the Gap: VAEs Perform Independent Mechanism Analysis

Variational autoencoders (VAEs) are a popular framework for modeling complex data distributions; they can be efficiently trained via variational inference by maximizing the evidence lower bound (ELBO), at the expense of a gap to the exact (log-)marginal likelihood. While VAEs are commonly used for representation learning, it is unclear why ELBO maximization would yield useful representations, since unregularized maximum likelihood estimation cannot invert the data-generating process. Yet, VAEs often succeed at this task. We seek to elucidate this apparent paradox by studying nonlinear VAEs in the limit of near-deterministic decoders. We first prove that, in this regime, the optimal encoder approximately inverts the decoder -- a commonly used but unproven conjecture -- which we refer to as {\em self-consistency}. Leveraging self-consistency, we show that the ELBO converges to a regularized log-likelihood. This allows VAEs to perform what has recently been termed independent mechanism analysis (IMA): it adds an inductive bias towards decoders with column-orthogonal Jacobians, which helps recovering the true latent factors. The gap between ELBO and log-likelihood is therefore welcome, since it bears unanticipated benefits for nonlinear representation learning. In experiments on synthetic and image data, we show that VAEs uncover the true latent factors when the data generating process satisfies the IMA assumption.

Bayesian Information Criterion for Event-based Multi-trial Ensemble data

Transient recurring phenomena are ubiquitous in many scientific fields like neuroscience and meteorology. Time inhomogenous Vector Autoregressive Models (VAR) may be used to characterize peri-event system dynamics associated with such phenomena, and can be learned by exploiting multi-dimensional data gathering samples of the evolution of the system in multiple time windows comprising, each associated with one occurrence of the transient phenomenon, that we will call "trial". However, optimal VAR model order selection methods, commonly relying on the Akaike or Bayesian Information Criteria (AIC/BIC), are typically not designed for multi-trial data. Here we derive the BIC methods for multi-trial ensemble data which are gathered after the detection of the events. We show using simulated bivariate AR models that the multi-trial BIC is able to recover the real model order. We also demonstrate with simulated transient events and real data that the multi-trial BIC is able to estimate a sufficiently small model order for dynamic system modeling.