NN-ResDMD: Learning Koopman Representations for Complex Dynamics with Spectral Residuals

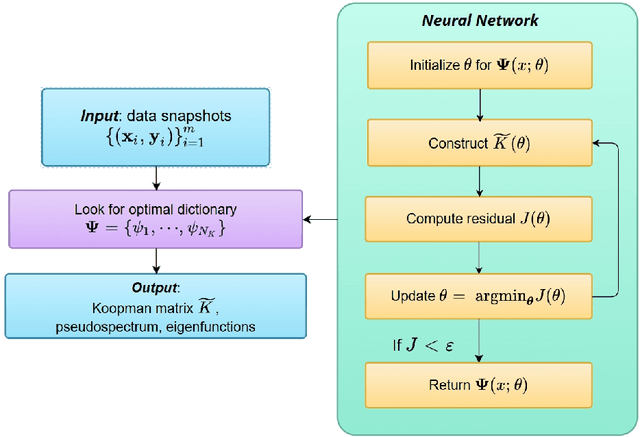
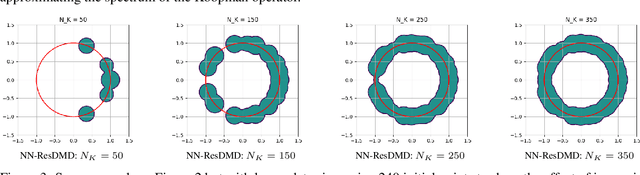
Analyzing long-term behaviors in high-dimensional nonlinear dynamical systems remains a significant challenge. The Koopman operator framework has emerged as a powerful tool to address this issue by providing a globally linear perspective on nonlinear dynamics. However, existing methods for approximating the Koopman operator and its spectral components, particularly in large-scale systems, often lack robust theoretical guarantees. Residual Dynamic Mode Decomposition (ResDMD) introduces a spectral residual measure to assess the convergence of the estimated Koopman spectrum, which helps filter out spurious spectral components. Nevertheless, it depends on pre-computed spectra, thereby inheriting their inaccuracies. To overcome its limitations, we introduce the Neural Network-ResDMD (NN-ResDMD), a method that directly estimates Koopman spectral components by minimizing the spectral residual. By leveraging neural networks, NN-ResDMD automatically identifies the optimal basis functions of the Koopman invariant subspace, eliminating the need for manual selection and improving the reliability of the analysis. Experiments on physical and biological systems demonstrate that NN-ResDMD significantly improves both accuracy and scalability, making it an effective tool for analyzing complex dynamical systems.

Information Theoretic Measures of Causal Influences during Transient Neural Events

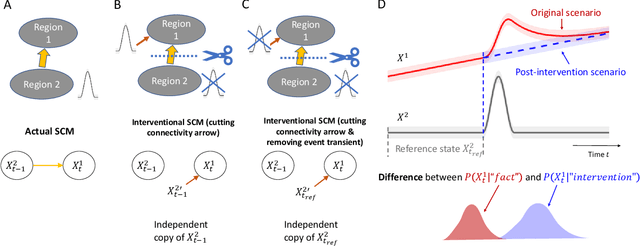
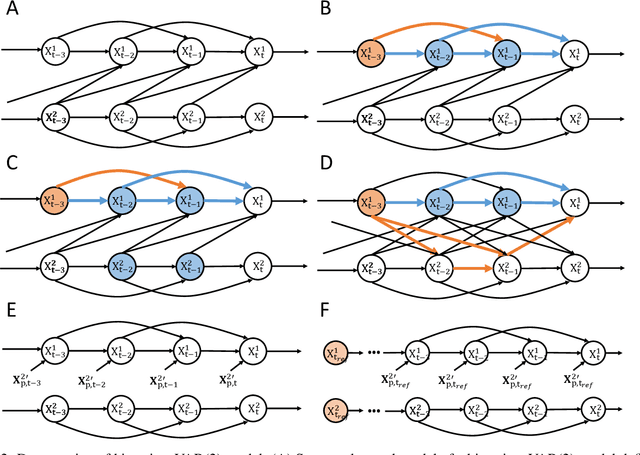
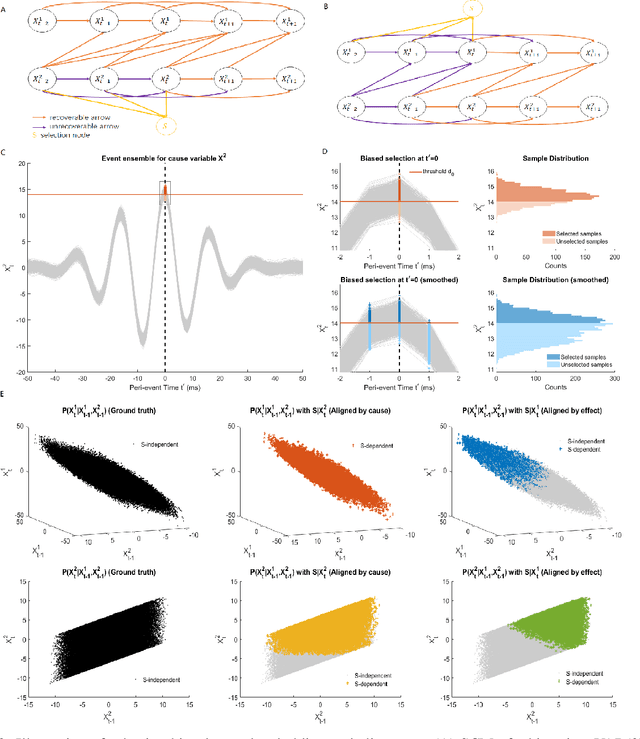
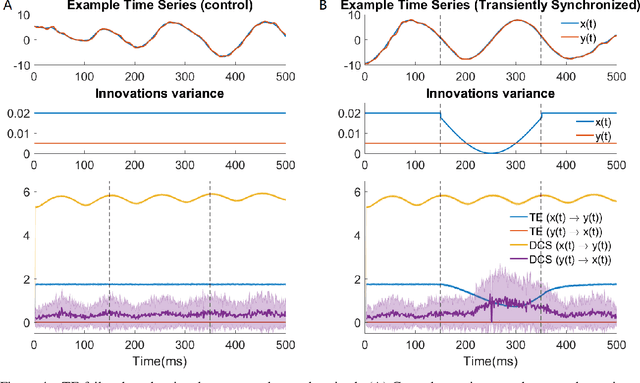
Transient phenomena play a key role in coordinating brain activity at multiple scales, however,their underlying mechanisms remain largely unknown. A key challenge for neural data science is thus to characterize the network interactions at play during these events. Using the formalism of Structural Causal Models and their graphical representation, we investigate the theoretical and empirical properties of Information Theory based causal strength measures in the context of recurring spontaneous transient events. After showing the limitations of Transfer Entropy and Dynamic Causal Strength in such a setting, we introduce a novel measure, relative Dynamic Causal Strength, and provide theoretical and empirical support for its benefits. These methods are applied to simulated and experimentally recorded neural time series, and provide results in agreement with our current understanding of the underlying brain circuits.

Bayesian Information Criterion for Event-based Multi-trial Ensemble data

Transient recurring phenomena are ubiquitous in many scientific fields like neuroscience and meteorology. Time inhomogenous Vector Autoregressive Models (VAR) may be used to characterize peri-event system dynamics associated with such phenomena, and can be learned by exploiting multi-dimensional data gathering samples of the evolution of the system in multiple time windows comprising, each associated with one occurrence of the transient phenomenon, that we will call "trial". However, optimal VAR model order selection methods, commonly relying on the Akaike or Bayesian Information Criteria (AIC/BIC), are typically not designed for multi-trial data. Here we derive the BIC methods for multi-trial ensemble data which are gathered after the detection of the events. We show using simulated bivariate AR models that the multi-trial BIC is able to recover the real model order. We also demonstrate with simulated transient events and real data that the multi-trial BIC is able to estimate a sufficiently small model order for dynamic system modeling.