Homomorphism Autoencoder -- Learning Group Structured Representations from Observed Transitions
Paper and Code
Jul 25, 2022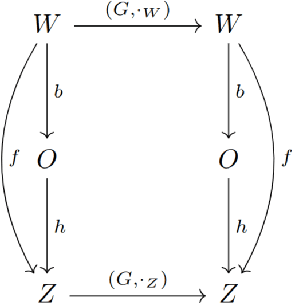

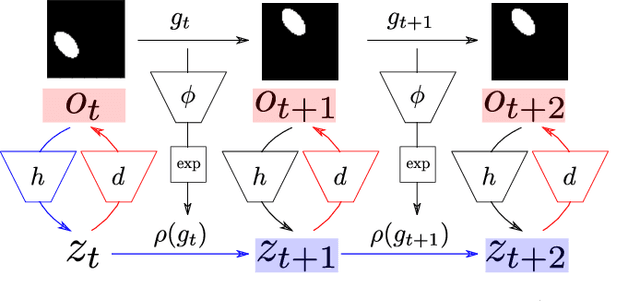

How can we acquire world models that veridically represent the outside world both in terms of what is there and in terms of how our actions affect it? Can we acquire such models by interacting with the world, and can we state mathematical desiderata for their relationship with a hypothetical reality existing outside our heads? As machine learning is moving towards representations containing not just observational but also interventional knowledge, we study these problems using tools from representation learning and group theory. Under the assumption that our actuators act upon the world, we propose methods to learn internal representations of not just sensory information but also of actions that modify our sensory representations in a way that is consistent with the actions and transitions in the world. We use an autoencoder equipped with a group representation linearly acting on its latent space, trained on 2-step reconstruction such as to enforce a suitable homomorphism property on the group representation. Compared to existing work, our approach makes fewer assumptions on the group representation and on which transformations the agent can sample from the group. We motivate our method theoretically, and demonstrate empirically that it can learn the correct representation of the groups and the topology of the environment. We also compare its performance in trajectory prediction with previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge