Homomorphism Autoencoder -- Learning Group Structured Representations from Observed Transitions

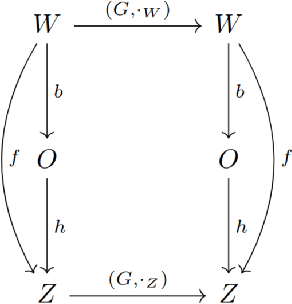
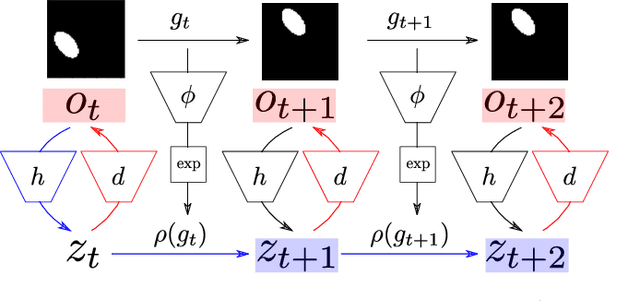
How can we acquire world models that veridically represent the outside world both in terms of what is there and in terms of how our actions affect it? Can we acquire such models by interacting with the world, and can we state mathematical desiderata for their relationship with a hypothetical reality existing outside our heads? As machine learning is moving towards representations containing not just observational but also interventional knowledge, we study these problems using tools from representation learning and group theory. Under the assumption that our actuators act upon the world, we propose methods to learn internal representations of not just sensory information but also of actions that modify our sensory representations in a way that is consistent with the actions and transitions in the world. We use an autoencoder equipped with a group representation linearly acting on its latent space, trained on 2-step reconstruction such as to enforce a suitable homomorphism property on the group representation. Compared to existing work, our approach makes fewer assumptions on the group representation and on which transformations the agent can sample from the group. We motivate our method theoretically, and demonstrate empirically that it can learn the correct representation of the groups and the topology of the environment. We also compare its performance in trajectory prediction with previous methods.

Uncertainty estimation under model misspecification in neural network regression

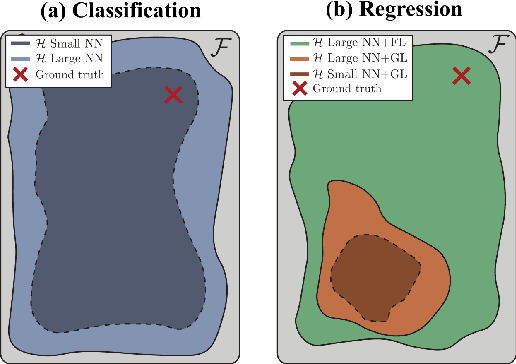
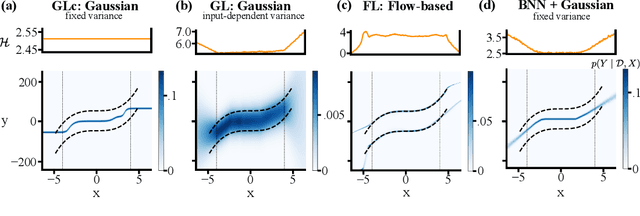
Although neural networks are powerful function approximators, the underlying modelling assumptions ultimately define the likelihood and thus the hypothesis class they are parameterizing. In classification, these assumptions are minimal as the commonly employed softmax is capable of representing any categorical distribution. In regression, however, restrictive assumptions on the type of continuous distribution to be realized are typically placed, like the dominant choice of training via mean-squared error and its underlying Gaussianity assumption. Recently, modelling advances allow to be agnostic to the type of continuous distribution to be modelled, granting regression the flexibility of classification models. While past studies stress the benefit of such flexible regression models in terms of performance, here we study the effect of the model choice on uncertainty estimation. We highlight that under model misspecification, aleatoric uncertainty is not properly captured, and that a Bayesian treatment of a misspecified model leads to unreliable epistemic uncertainty estimates. Overall, our study provides an overview on how modelling choices in regression may influence uncertainty estimation and thus any downstream decision making process.