Estimating Joint interventional distributions from marginal interventional data

In this paper we show how to exploit interventional data to acquire the joint conditional distribution of all the variables using the Maximum Entropy principle. To this end, we extend the Causal Maximum Entropy method to make use of interventional data in addition to observational data. Using Lagrange duality, we prove that the solution to the Causal Maximum Entropy problem with interventional constraints lies in the exponential family, as in the Maximum Entropy solution. Our method allows us to perform two tasks of interest when marginal interventional distributions are provided for any subset of the variables. First, we show how to perform causal feature selection from a mixture of observational and single-variable interventional data, and, second, how to infer joint interventional distributions. For the former task, we show on synthetically generated data, that our proposed method outperforms the state-of-the-art method on merging datasets, and yields comparable results to the KCI-test which requires access to joint observations of all variables.

Targeted Reduction of Causal Models

Why does a phenomenon occur? Addressing this question is central to most scientific inquiries based on empirical observations, and often heavily relies on simulations of scientific models. As models become more intricate, deciphering the causes behind these phenomena in high-dimensional spaces of interconnected variables becomes increasingly challenging. Causal machine learning may assist scientists in the discovery of relevant and interpretable patterns of causation in simulations. We introduce Targeted Causal Reduction (TCR), a method for turning complex models into a concise set of causal factors that explain a specific target phenomenon. We derive an information theoretic objective to learn TCR from interventional data or simulations and propose algorithms to optimize this objective efficiently. TCR's ability to generate interpretable high-level explanations from complex models is demonstrated on toy and mechanical systems, illustrating its potential to assist scientists in the study of complex phenomena in a broad range of disciplines.

Nonparametric Identifiability of Causal Representations from Unknown Interventions

We study causal representation learning, the task of inferring latent causal variables and their causal relations from high-dimensional functions ("mixtures") of the variables. Prior work relies on weak supervision, in the form of counterfactual pre- and post-intervention views or temporal structure; places restrictive assumptions, such as linearity, on the mixing function or latent causal model; or requires partial knowledge of the generative process, such as the causal graph or the intervention targets. We instead consider the general setting in which both the causal model and the mixing function are nonparametric. The learning signal takes the form of multiple datasets, or environments, arising from unknown interventions in the underlying causal model. Our goal is to identify both the ground truth latents and their causal graph up to a set of ambiguities which we show to be irresolvable from interventional data. We study the fundamental setting of two causal variables and prove that the observational distribution and one perfect intervention per node suffice for identifiability, subject to a genericity condition. This condition rules out spurious solutions that involve fine-tuning of the intervened and observational distributions, mirroring similar conditions for nonlinear cause-effect inference. For an arbitrary number of variables, we show that two distinct paired perfect interventions per node guarantee identifiability. Further, we demonstrate that the strengths of causal influences among the latent variables are preserved by all equivalent solutions, rendering the inferred representation appropriate for drawing causal conclusions from new data. Our study provides the first identifiability results for the general nonparametric setting with unknown interventions, and elucidates what is possible and impossible for causal representation learning without more direct supervision.

Causal Component Analysis

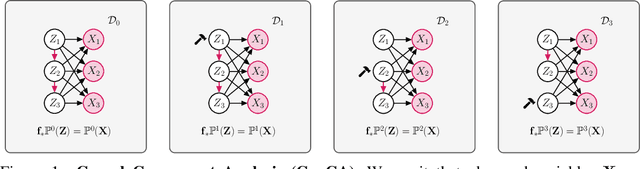
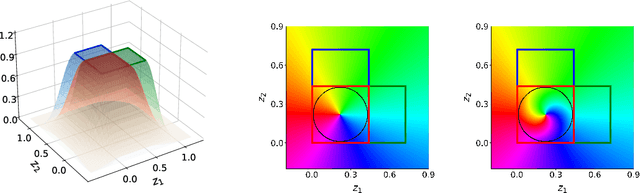
Independent Component Analysis (ICA) aims to recover independent latent variables from observed mixtures thereof. Causal Representation Learning (CRL) aims instead to infer causally related (thus often statistically dependent) latent variables, together with the unknown graph encoding their causal relationships. We introduce an intermediate problem termed Causal Component Analysis (CauCA). CauCA can be viewed as a generalization of ICA, modelling the causal dependence among the latent components, and as a special case of CRL. In contrast to CRL, it presupposes knowledge of the causal graph, focusing solely on learning the unmixing function and the causal mechanisms. Any impossibility results regarding the recovery of the ground truth in CauCA also apply for CRL, while possibility results may serve as a stepping stone for extensions to CRL. We characterize CauCA identifiability from multiple datasets generated through different types of interventions on the latent causal variables. As a corollary, this interventional perspective also leads to new identifiability results for nonlinear ICA -- a special case of CauCA with an empty graph -- requiring strictly fewer datasets than previous results. We introduce a likelihood-based approach using normalizing flows to estimate both the unmixing function and the causal mechanisms, and demonstrate its effectiveness through extensive synthetic experiments in the CauCA and ICA setting.

Deep Learning based Forecasting: a case study from the online fashion industry

Demand forecasting in the online fashion industry is particularly amendable to global, data-driven forecasting models because of the industry's set of particular challenges. These include the volume of data, the irregularity, the high amount of turn-over in the catalog and the fixed inventory assumption. While standard deep learning forecasting approaches cater for many of these, the fixed inventory assumption requires a special treatment via controlling the relationship between price and demand closely. In this case study, we describe the data and our modelling approach for this forecasting problem in detail and present empirical results that highlight the effectiveness of our approach.

Evaluating vaccine allocation strategies using simulation-assisted causal modelling

Early on during a pandemic, vaccine availability is limited, requiring prioritisation of different population groups. Evaluating vaccine allocation is therefore a crucial element of pandemics response. In the present work, we develop a model to retrospectively evaluate age-dependent counterfactual vaccine allocation strategies against the COVID-19 pandemic. To estimate the effect of allocation on the expected severe-case incidence, we employ a simulation-assisted causal modelling approach which combines a compartmental infection-dynamics simulation, a coarse-grained, data-driven causal model and literature estimates for immunity waning. We compare Israel's implemented vaccine allocation strategy in 2021 to counterfactual strategies such as no prioritisation, prioritisation of younger age groups or a strict risk-ranked approach; we find that Israel's implemented strategy was indeed highly effective. We also study the marginal impact of increasing vaccine uptake for a given age group and find that increasing vaccinations in the elderly is most effective at preventing severe cases, whereas additional vaccinations for middle-aged groups reduce infections most effectively. Due to its modular structure, our model can easily be adapted to study future pandemics. We demonstrate this flexibility by investigating vaccine allocation strategies for a pandemic with characteristics of the Spanish Flu. Our approach thus helps evaluate vaccination strategies under the complex interplay of core epidemic factors, including age-dependent risk profiles, immunity waning, vaccine availability and spreading rates.

DCI-ES: An Extended Disentanglement Framework with Connections to Identifiability

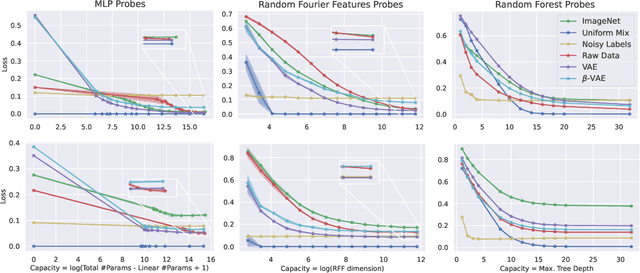
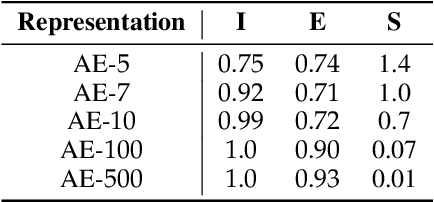
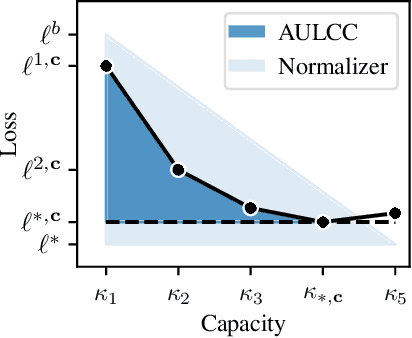
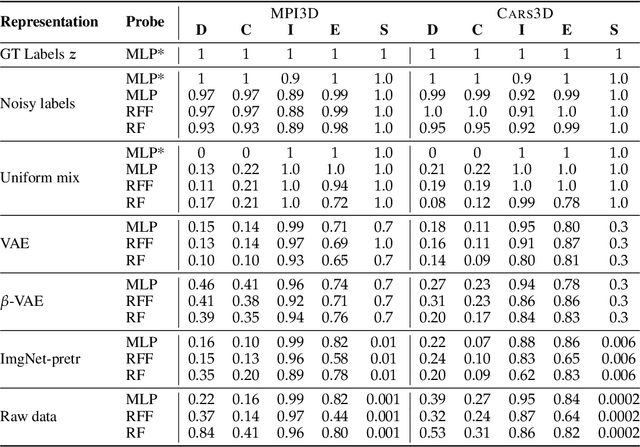
In representation learning, a common approach is to seek representations which disentangle the underlying factors of variation. Eastwood & Williams (2018) proposed three metrics for quantifying the quality of such disentangled representations: disentanglement (D), completeness (C) and informativeness (I). In this work, we first connect this DCI framework to two common notions of linear and nonlinear identifiability, thus establishing a formal link between disentanglement and the closely-related field of independent component analysis. We then propose an extended DCI-ES framework with two new measures of representation quality - explicitness (E) and size (S) - and point out how D and C can be computed for black-box predictors. Our main idea is that the functional capacity required to use a representation is an important but thus-far neglected aspect of representation quality, which we quantify using explicitness or ease-of-use (E). We illustrate the relevance of our extensions on the MPI3D and Cars3D datasets.