Estimating Joint interventional distributions from marginal interventional data

In this paper we show how to exploit interventional data to acquire the joint conditional distribution of all the variables using the Maximum Entropy principle. To this end, we extend the Causal Maximum Entropy method to make use of interventional data in addition to observational data. Using Lagrange duality, we prove that the solution to the Causal Maximum Entropy problem with interventional constraints lies in the exponential family, as in the Maximum Entropy solution. Our method allows us to perform two tasks of interest when marginal interventional distributions are provided for any subset of the variables. First, we show how to perform causal feature selection from a mixture of observational and single-variable interventional data, and, second, how to infer joint interventional distributions. For the former task, we show on synthetically generated data, that our proposed method outperforms the state-of-the-art method on merging datasets, and yields comparable results to the KCI-test which requires access to joint observations of all variables.

Root Cause Analysis of Outliers with Missing Structural Knowledge

Recent work conceptualized root cause analysis (RCA) of anomalies via quantitative contribution analysis using causal counterfactuals in structural causal models (SCMs). The framework comes with three practical challenges: (1) it requires the causal directed acyclic graph (DAG), together with an SCM, (2) it is statistically ill-posed since it probes regression models in regions of low probability density, (3) it relies on Shapley values which are computationally expensive to find. In this paper, we propose simplified, efficient methods of root cause analysis when the task is to identify a unique root cause instead of quantitative contribution analysis. Our proposed methods run in linear order of SCM nodes and they require only the causal DAG without counterfactuals. Furthermore, for those use cases where the causal DAG is unknown, we justify the heuristic of identifying root causes as the variables with the highest anomaly score.

Phenomenological Causality

Discussions on causal relations in real life often consider variables for which the definition of causality is unclear since the notion of interventions on the respective variables is obscure. Asking 'what qualifies an action for being an intervention on the variable X' raises the question whether the action impacted all other variables only through X or directly, which implicitly refers to a causal model. To avoid this known circularity, we instead suggest a notion of 'phenomenological causality' whose basic concept is a set of elementary actions. Then the causal structure is defined such that elementary actions change only the causal mechanism at one node (e.g. one of the causal conditionals in the Markov factorization). This way, the Principle of Independent Mechanisms becomes the defining property of causal structure in domains where causality is a more abstract phenomenon rather than being an objective fact relying on hard-wired causal links between tangible objects. We describe this phenomenological approach to causality for toy and hypothetical real-world examples and argue that it is consistent with the causal Markov condition when the system under consideration interacts with other variables that control the elementary actions.

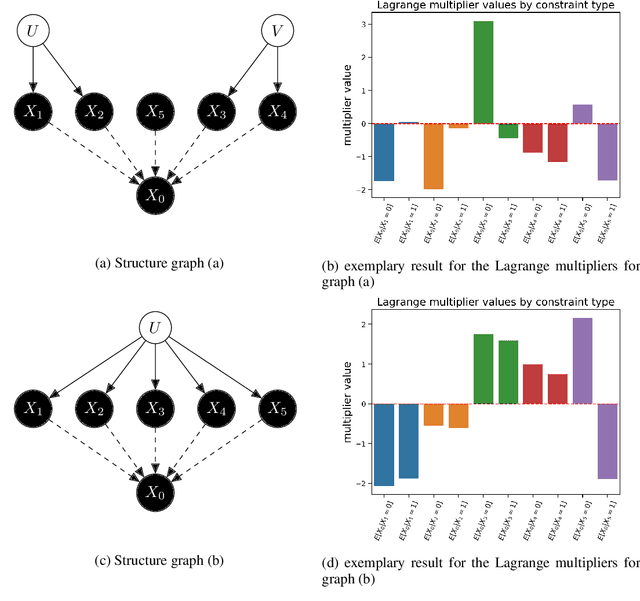
Obtaining Causal Information by Merging Datasets with MAXENT

The investigation of the question "which treatment has a causal effect on a target variable?" is of particular relevance in a large number of scientific disciplines. This challenging task becomes even more difficult if not all treatment variables were or even cannot be observed jointly with the target variable. Another similarly important and challenging task is to quantify the causal influence of a treatment on a target in the presence of confounders. In this paper, we discuss how causal knowledge can be obtained without having observed all variables jointly, but by merging the statistical information from different datasets. We first show how the maximum entropy principle can be used to identify edges among random variables when assuming causal sufficiency and an extended version of faithfulness. Additionally, we derive bounds on the interventional distribution and the average causal effect of a treatment on a target variable in the presence of confounders. In both cases we assume that only subsets of the variables have been observed jointly.