$β$-calibration of Language Model Confidence Scores for Generative QA

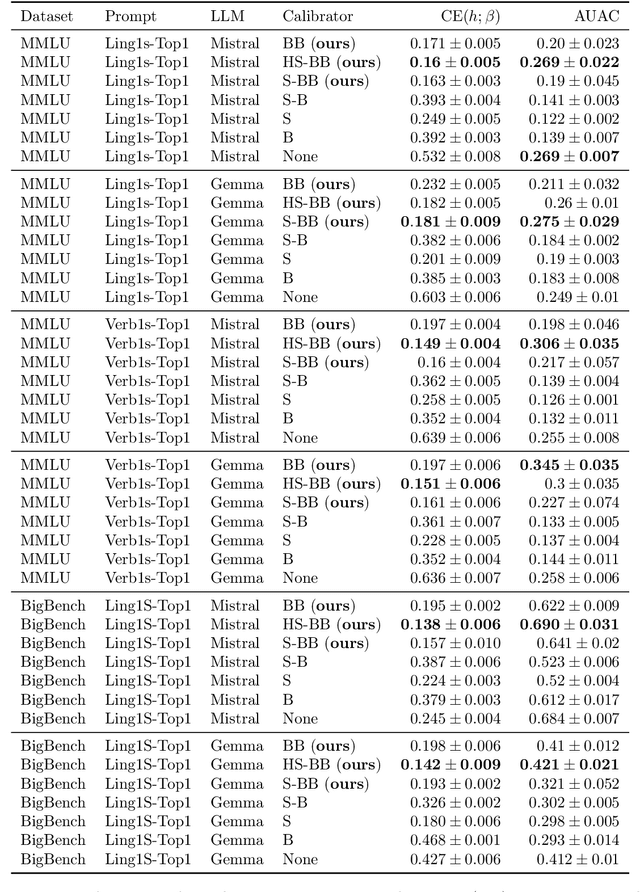
To use generative question-and-answering (QA) systems for decision-making and in any critical application, these systems need to provide well-calibrated confidence scores that reflect the correctness of their answers. Existing calibration methods aim to ensure that the confidence score is on average indicative of the likelihood that the answer is correct. We argue, however, that this standard (average-case) notion of calibration is difficult to interpret for decision-making in generative QA. To address this, we generalize the standard notion of average calibration and introduce $\beta$-calibration, which ensures calibration holds across different question-and-answer groups. We then propose discretized posthoc calibration schemes for achieving $\beta$-calibration.

Estimating Joint interventional distributions from marginal interventional data

In this paper we show how to exploit interventional data to acquire the joint conditional distribution of all the variables using the Maximum Entropy principle. To this end, we extend the Causal Maximum Entropy method to make use of interventional data in addition to observational data. Using Lagrange duality, we prove that the solution to the Causal Maximum Entropy problem with interventional constraints lies in the exponential family, as in the Maximum Entropy solution. Our method allows us to perform two tasks of interest when marginal interventional distributions are provided for any subset of the variables. First, we show how to perform causal feature selection from a mixture of observational and single-variable interventional data, and, second, how to infer joint interventional distributions. For the former task, we show on synthetically generated data, that our proposed method outperforms the state-of-the-art method on merging datasets, and yields comparable results to the KCI-test which requires access to joint observations of all variables.

Score matching through the roof: linear, nonlinear, and latent variables causal discovery

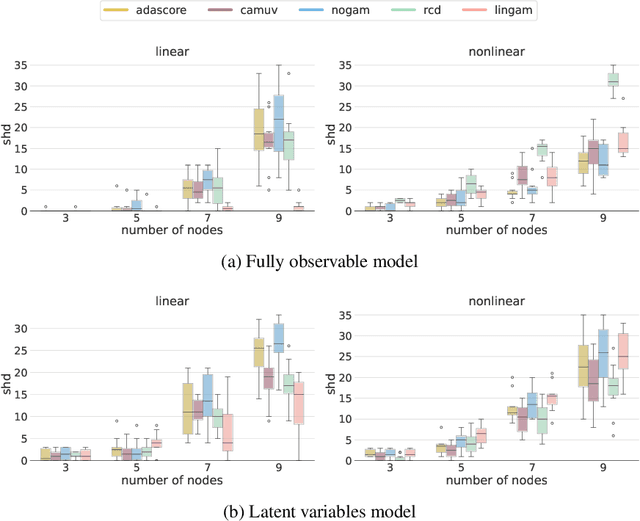
Causal discovery from observational data holds great promise, but existing methods rely on strong assumptions about the underlying causal structure, often requiring full observability of all relevant variables. We tackle these challenges by leveraging the score function $\nabla \log p(X)$ of observed variables for causal discovery and propose the following contributions. First, we generalize the existing results of identifiability with the score to additive noise models with minimal requirements on the causal mechanisms. Second, we establish conditions for inferring causal relations from the score even in the presence of hidden variables; this result is two-faced: we demonstrate the score's potential as an alternative to conditional independence tests to infer the equivalence class of causal graphs with hidden variables, and we provide the necessary conditions for identifying direct causes in latent variable models. Building on these insights, we propose a flexible algorithm for causal discovery across linear, nonlinear, and latent variable models, which we empirically validate.

The PetShop Dataset -- Finding Causes of Performance Issues across Microservices

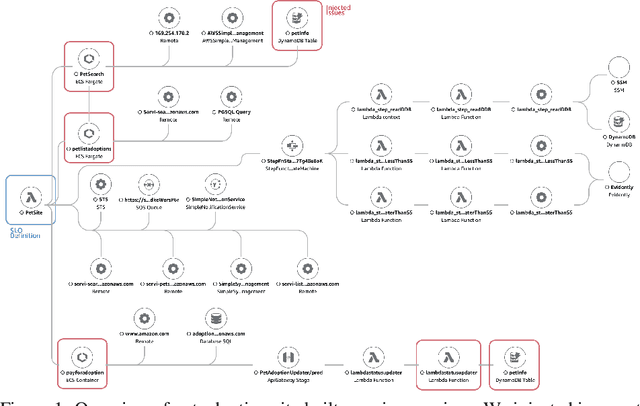
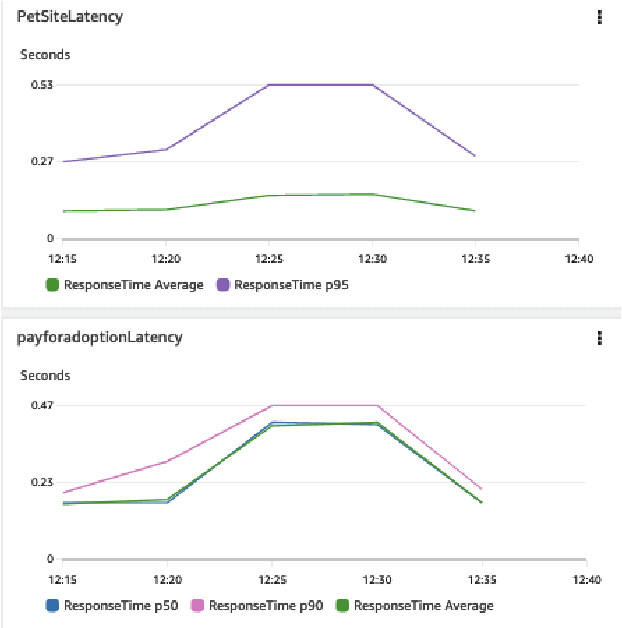
Identifying root causes for unexpected or undesirable behavior in complex systems is a prevalent challenge. This issue becomes especially crucial in modern cloud applications that employ numerous microservices. Although the machine learning and systems research communities have proposed various techniques to tackle this problem, there is currently a lack of standardized datasets for quantitative benchmarking. Consequently, research groups are compelled to create their own datasets for experimentation. This paper introduces a dataset specifically designed for evaluating root cause analyses in microservice-based applications. The dataset encompasses latency, requests, and availability metrics emitted in 5-minute intervals from a distributed application. In addition to normal operation metrics, the dataset includes 68 injected performance issues, which increase latency and reduce availability throughout the system. We showcase how this dataset can be used to evaluate the accuracy of a variety of methods spanning different causal and non-causal characterisations of the root cause analysis problem. We hope the new dataset, available at https://github.com/amazon-science/petshop-root-cause-analysis/ enables further development of techniques in this important area.

Beyond Single-Feature Importance with ICECREAM

Which set of features was responsible for a certain output of a machine learning model? Which components caused the failure of a cloud computing application? These are just two examples of questions we are addressing in this work by Identifying Coalition-based Explanations for Common and Rare Events in Any Model (ICECREAM). Specifically, we propose an information-theoretic quantitative measure for the influence of a coalition of variables on the distribution of a target variable. This allows us to identify which set of factors is essential to obtain a certain outcome, as opposed to well-established explainability and causal contribution analysis methods which can assign contributions only to individual factors and rank them by their importance. In experiments with synthetic and real-world data, we show that ICECREAM outperforms state-of-the-art methods for explainability and root cause analysis, and achieves impressive accuracy in both tasks.

Causal Inference Through the Structural Causal Marginal Problem

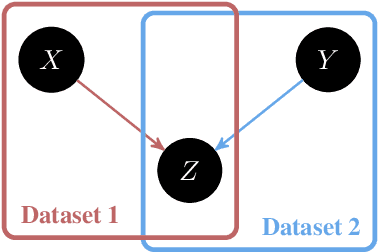
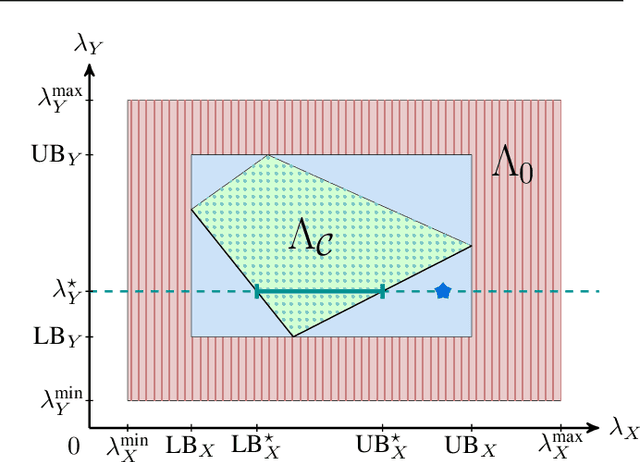
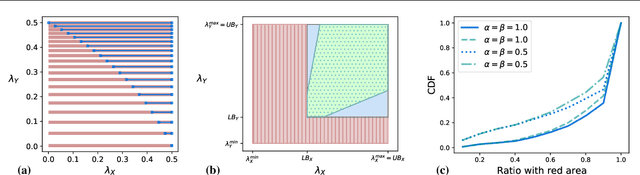
We introduce an approach to counterfactual inference based on merging information from multiple datasets. We consider a causal reformulation of the statistical marginal problem: given a collection of marginal structural causal models (SCMs) over distinct but overlapping sets of variables, determine the set of joint SCMs that are counterfactually consistent with the marginal ones. We formalise this approach for categorical SCMs using the response function formulation and show that it reduces the space of allowed marginal and joint SCMs. Our work thus highlights a new mode of falsifiability through additional variables, in contrast to the statistical one via additional data.

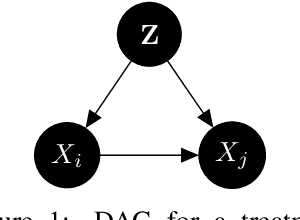
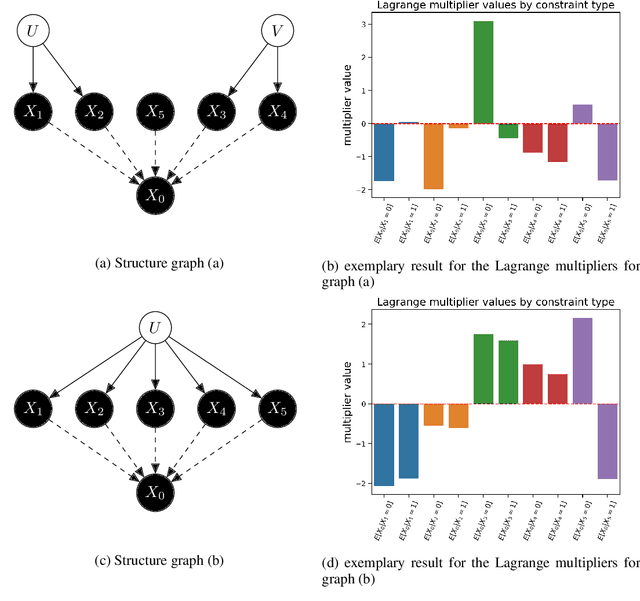
Obtaining Causal Information by Merging Datasets with MAXENT

The investigation of the question "which treatment has a causal effect on a target variable?" is of particular relevance in a large number of scientific disciplines. This challenging task becomes even more difficult if not all treatment variables were or even cannot be observed jointly with the target variable. Another similarly important and challenging task is to quantify the causal influence of a treatment on a target in the presence of confounders. In this paper, we discuss how causal knowledge can be obtained without having observed all variables jointly, but by merging the statistical information from different datasets. We first show how the maximum entropy principle can be used to identify edges among random variables when assuming causal sufficiency and an extended version of faithfulness. Additionally, we derive bounds on the interventional distribution and the average causal effect of a treatment on a target variable in the presence of confounders. In both cases we assume that only subsets of the variables have been observed jointly.

DISCo for the CIA: Deep learning, Instance Segmentation, and Correlations for Calcium Imaging Analysis

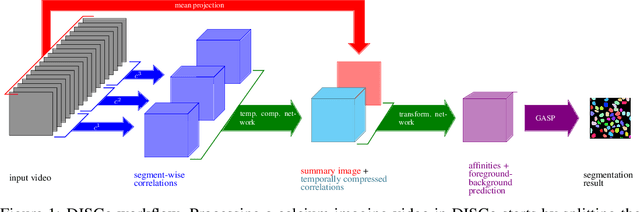
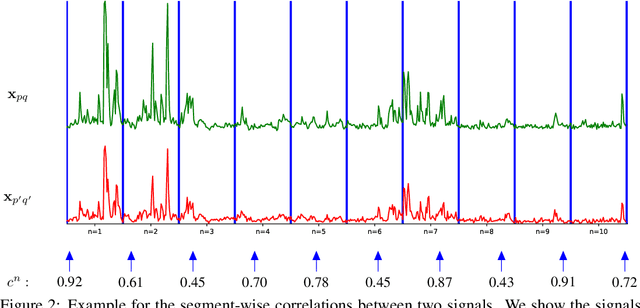
Calcium imaging is one of the most important tools in neurophysiology as it enables the observation of neuronal activity for hundreds of cells in parallel and at single-cell resolution. In order to use the data gained with calcium imaging, it is necessary to extract individual cells and their activity from the recordings. Although many sophisticated methods have been proposed, the cell extraction from calcium imaging data can still be prohibitively laborious and require manual annotation and correction. We present DISCo, a novel approach for the cell segmentation in Calcium Imaging Analysis (CIA) that combines the advantages of Deep learning with a state-of-the-art Instance Segmentation algorithm and uses temporal information from the recordings in a computationally efficient way by computing Correlations between pixels.