Clustering by Denoising: Latent plug-and-play diffusion for single-cell data

Single-cell RNA sequencing (scRNA-seq) enables the study of cellular heterogeneity. Yet, clustering accuracy, and with it downstream analyses based on cell labels, remain challenging due to measurement noise and biological variability. In standard latent spaces (e.g., obtained through PCA), data from different cell types can be projected close together, making accurate clustering difficult. We introduce a latent plug-and-play diffusion framework that separates the observation and denoising space. This separation is operationalized through a novel Gibbs sampling procedure: the learned diffusion prior is applied in a low-dimensional latent space to perform denoising, while to steer this process, noise is reintroduced into the original high-dimensional observation space. This unique "input-space steering" ensures the denoising trajectory remains faithful to the original data structure. Our approach offers three key advantages: (1) adaptive noise handling via a tunable balance between prior and observed data; (2) uncertainty quantification through principled uncertainty estimates for downstream analysis; and (3) generalizable denoising by leveraging clean reference data to denoise noisier datasets, and via averaging, improve quality beyond the training set. We evaluate robustness on both synthetic and real single-cell genomics data. Our method improves clustering accuracy on synthetic data across varied noise levels and dataset shifts. On real-world single-cell data, our method demonstrates improved biological coherence in the resulting cell clusters, with cluster boundaries that better align with known cell type markers and developmental trajectories.

From Guess2Graph: When and How Can Unreliable Experts Safely Boost Causal Discovery in Finite Samples?

Causal discovery algorithms often perform poorly with limited samples. While integrating expert knowledge (including from LLMs) as constraints promises to improve performance, guarantees for existing methods require perfect predictions or uncertainty estimates, making them unreliable for practical use. We propose the Guess2Graph (G2G) framework, which uses expert guesses to guide the sequence of statistical tests rather than replacing them. This maintains statistical consistency while enabling performance improvements. We develop two instantiations of G2G: PC-Guess, which augments the PC algorithm, and gPC-Guess, a learning-augmented variant designed to better leverage high-quality expert input. Theoretically, both preserve correctness regardless of expert error, with gPC-Guess provably outperforming its non-augmented counterpart in finite samples when experts are "better than random." Empirically, both show monotonic improvement with expert accuracy, with gPC-Guess achieving significantly stronger gains.

Federated Causal Inference in Healthcare: Methods, Challenges, and Applications

Federated causal inference enables multi-site treatment effect estimation without sharing individual-level data, offering a privacy-preserving solution for real-world evidence generation. However, data heterogeneity across sites, manifested in differences in covariate, treatment, and outcome, poses significant challenges for unbiased and efficient estimation. In this paper, we present a comprehensive review and theoretical analysis of federated causal effect estimation across both binary/continuous and time-to-event outcomes. We classify existing methods into weight-based strategies and optimization-based frameworks and further discuss extensions including personalized models, peer-to-peer communication, and model decomposition. For time-to-event outcomes, we examine federated Cox and Aalen-Johansen models, deriving asymptotic bias and variance under heterogeneity. Our analysis reveals that FedProx-style regularization achieves near-optimal bias-variance trade-offs compared to naive averaging and meta-analysis. We review related software tools and conclude by outlining opportunities, challenges, and future directions for scalable, fair, and trustworthy federated causal inference in distributed healthcare systems.

MOSIC: Model-Agnostic Optimal Subgroup Identification with Multi-Constraint for Improved Reliability

Identifying subgroups that benefit from specific treatments using observational data is a critical challenge in personalized medicine. Most existing approaches solely focus on identifying a subgroup with an improved treatment effect. However, practical considerations, such as ensuring a minimum subgroup size for representativeness or achieving sufficient confounder balance for reliability, are also important for making findings clinically meaningful and actionable. While some studies address these constraints individually, none offer a unified approach to handle them simultaneously. To bridge this gap, we propose a model-agnostic framework for optimal subgroup identification under multiple constraints. We reformulate this combinatorial problem as an unconstrained min-max optimization problem with novel modifications and solve it by a gradient descent ascent algorithm. We further prove its convergence to a feasible and locally optimal solution. Our method is stable and highly flexible, supporting various models and techniques for estimating and optimizing treatment effectiveness with observational data. Extensive experiments on both synthetic and real-world datasets demonstrate its effectiveness in identifying subgroups that satisfy multiple constraints, achieving higher treatment effects and better confounder balancing results across different group sizes.

From Restless to Contextual: A Thresholding Bandit Approach to Improve Finite-horizon Performance

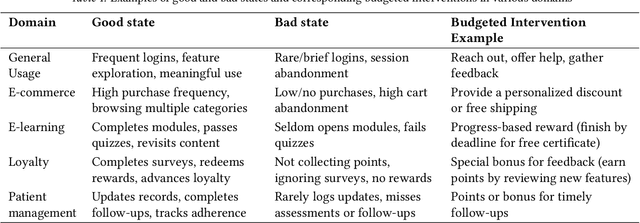
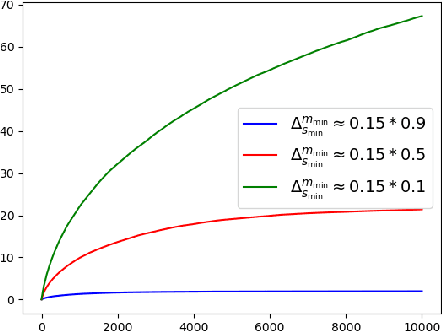
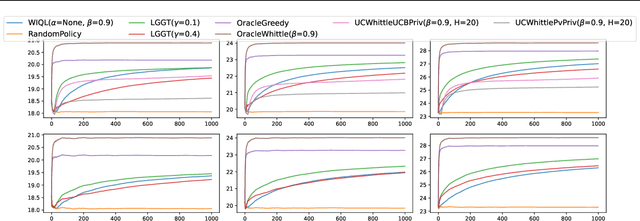
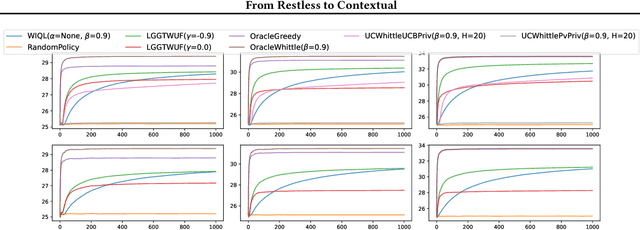
Online restless bandits extend classic contextual bandits by incorporating state transitions and budget constraints, representing each agent as a Markov Decision Process (MDP). This framework is crucial for finite-horizon strategic resource allocation, optimizing limited costly interventions for long-term benefits. However, learning the underlying MDP for each agent poses a major challenge in finite-horizon settings. To facilitate learning, we reformulate the problem as a scalable budgeted thresholding contextual bandit problem, carefully integrating the state transitions into the reward design and focusing on identifying agents with action benefits exceeding a threshold. We establish the optimality of an oracle greedy solution in a simple two-state setting, and propose an algorithm that achieves minimax optimal constant regret in the online multi-state setting with heterogeneous agents and knowledge of outcomes under no intervention. We numerically show that our algorithm outperforms existing online restless bandit methods, offering significant improvements in finite-horizon performance.

Reward Maximization for Pure Exploration: Minimax Optimal Good Arm Identification for Nonparametric Multi-Armed Bandits

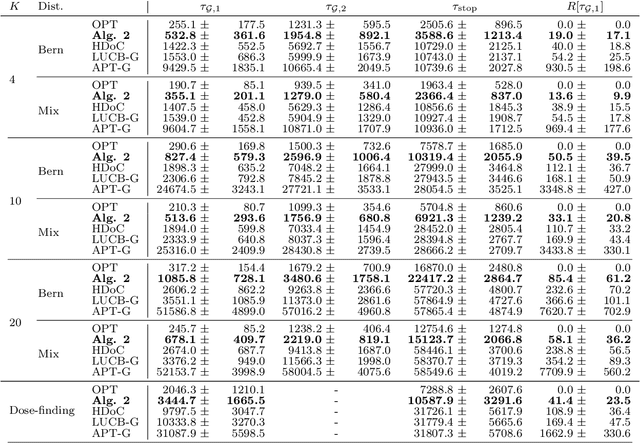
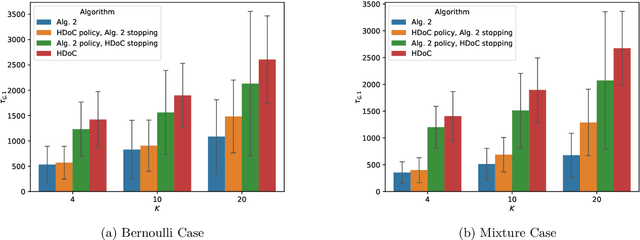
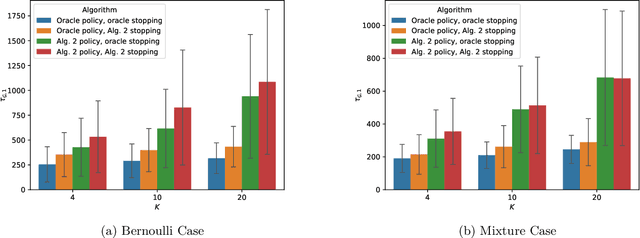
In multi-armed bandits, the tasks of reward maximization and pure exploration are often at odds with each other. The former focuses on exploiting arms with the highest means, while the latter may require constant exploration across all arms. In this work, we focus on good arm identification (GAI), a practical bandit inference objective that aims to label arms with means above a threshold as quickly as possible. We show that GAI can be efficiently solved by combining a reward-maximizing sampling algorithm with a novel nonparametric anytime-valid sequential test for labeling arm means. We first establish that our sequential test maintains error control under highly nonparametric assumptions and asymptotically achieves the minimax optimal e-power, a notion of power for anytime-valid tests. Next, by pairing regret-minimizing sampling schemes with our sequential test, we provide an approach that achieves minimax optimal stopping times for labeling arms with means above a threshold, under an error probability constraint. Our empirical results validate our approach beyond the minimax setting, reducing the expected number of samples for all stopping times by at least 50% across both synthetic and real-world settings.

LoSAM: Local Search in Additive Noise Models with Unmeasured Confounders, a Top-Down Global Discovery Approach

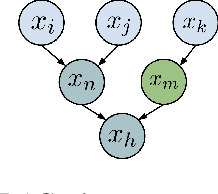
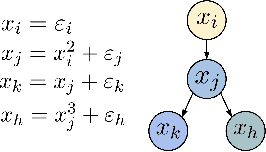
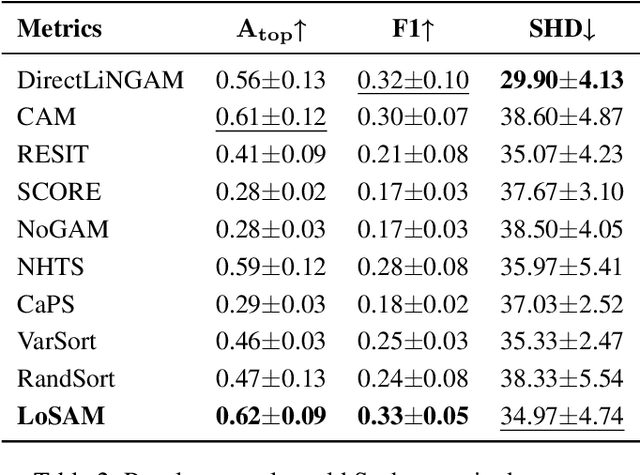
We address the challenge of causal discovery in structural equation models with additive noise without imposing additional assumptions on the underlying data-generating process. We introduce local search in additive noise model (LoSAM), which generalizes an existing nonlinear method that leverages local causal substructures to the general additive noise setting, allowing for both linear and nonlinear causal mechanisms. We show that LoSAM achieves polynomial runtime, and improves runtime and efficiency by exploiting new substructures to minimize the conditioning set at each step. Further, we introduce a variant of LoSAM, LoSAM-UC, that is robust to unmeasured confounding among roots, a property that is often not satisfied by functional-causal-model-based methods. We numerically demonstrate the utility of LoSAM, showing that it outperforms existing benchmarks.

CSPI-MT: Calibrated Safe Policy Improvement with Multiple Testing for Threshold Policies

When modifying existing policies in high-risk settings, it is often necessary to ensure with high certainty that the newly proposed policy improves upon a baseline, such as the status quo. In this work, we consider the problem of safe policy improvement, where one only adopts a new policy if it is deemed to be better than the specified baseline with at least pre-specified probability. We focus on threshold policies, a ubiquitous class of policies with applications in economics, healthcare, and digital advertising. Existing methods rely on potentially underpowered safety checks and limit the opportunities for finding safe improvements, so too often they must revert to the baseline to maintain safety. We overcome these issues by leveraging the most powerful safety test in the asymptotic regime and allowing for multiple candidates to be tested for improvement over the baseline. We show that in adversarial settings, our approach controls the rate of adopting a policy worse than the baseline to the pre-specified error level, even in moderate sample sizes. We present CSPI and CSPI-MT, two novel heuristics for selecting cutoff(s) to maximize the policy improvement from baseline. We demonstrate through both synthetic and external datasets that our approaches improve both the detection rates of safe policies and the realized improvement, particularly under stringent safety requirements and low signal-to-noise conditions.

Hybrid Global Causal Discovery with Local Search

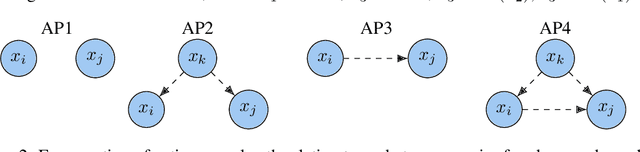
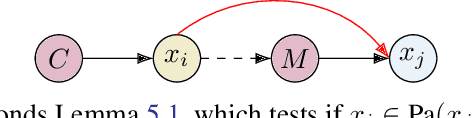
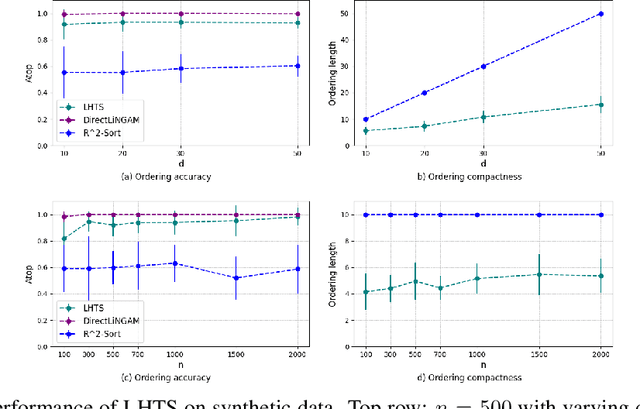
Learning the unique directed acyclic graph corresponding to an unknown causal model is a challenging task. Methods based on functional causal models can identify a unique graph, but either suffer from the curse of dimensionality or impose strong parametric assumptions. To address these challenges, we propose a novel hybrid approach for global causal discovery in observational data that leverages local causal substructures. We first present a topological sorting algorithm that leverages ancestral relationships in linear structural equation models to establish a compact top-down hierarchical ordering, encoding more causal information than linear orderings produced by existing methods. We demonstrate that this approach generalizes to nonlinear settings with arbitrary noise. We then introduce a nonparametric constraint-based algorithm that prunes spurious edges by searching for local conditioning sets, achieving greater accuracy than current methods. We provide theoretical guarantees for correctness and worst-case polynomial time complexities, with empirical validation on synthetic data.

Local Causal Discovery for Structural Evidence of Direct Discrimination

Fairness is a critical objective in policy design and algorithmic decision-making. Identifying the causal pathways of unfairness requires knowledge of the underlying structural causal model, which may be incomplete or unavailable. This limits the practicality of causal fairness analysis in complex or low-knowledge domains. To mitigate this practicality gap, we advocate for developing efficient causal discovery methods for fairness applications. To this end, we introduce local discovery for direct discrimination (LD3): a polynomial-time algorithm that recovers structural evidence of direct discrimination. LD3 performs a linear number of conditional independence tests with respect to variable set size. Moreover, we propose a graphical criterion for identifying the weighted controlled direct effect (CDE), a qualitative measure of direct discrimination. We prove that this criterion is satisfied by the knowledge returned by LD3, increasing the accessibility of the weighted CDE as a causal fairness measure. Taking liver transplant allocation as a case study, we highlight the potential impact of LD3 for modeling fairness in complex decision systems. Results on real-world data demonstrate more plausible causal relations than baselines, which took 197x to 5870x longer to execute.