Israel Nir
CSPI-MT: Calibrated Safe Policy Improvement with Multiple Testing for Threshold Policies
Aug 21, 2024


Abstract:When modifying existing policies in high-risk settings, it is often necessary to ensure with high certainty that the newly proposed policy improves upon a baseline, such as the status quo. In this work, we consider the problem of safe policy improvement, where one only adopts a new policy if it is deemed to be better than the specified baseline with at least pre-specified probability. We focus on threshold policies, a ubiquitous class of policies with applications in economics, healthcare, and digital advertising. Existing methods rely on potentially underpowered safety checks and limit the opportunities for finding safe improvements, so too often they must revert to the baseline to maintain safety. We overcome these issues by leveraging the most powerful safety test in the asymptotic regime and allowing for multiple candidates to be tested for improvement over the baseline. We show that in adversarial settings, our approach controls the rate of adopting a policy worse than the baseline to the pre-specified error level, even in moderate sample sizes. We present CSPI and CSPI-MT, two novel heuristics for selecting cutoff(s) to maximize the policy improvement from baseline. We demonstrate through both synthetic and external datasets that our approaches improve both the detection rates of safe policies and the realized improvement, particularly under stringent safety requirements and low signal-to-noise conditions.
Efficient Heterogeneous Treatment Effect Estimation With Multiple Experiments and Multiple Outcomes
Jun 10, 2022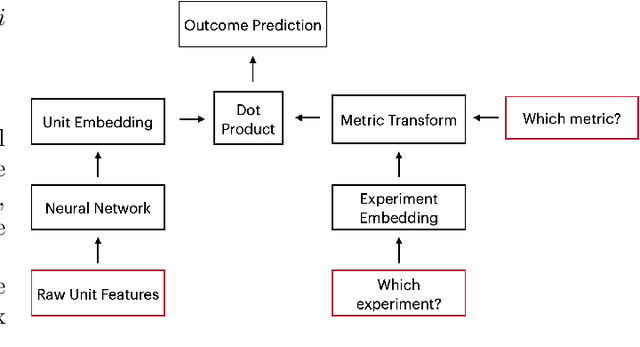
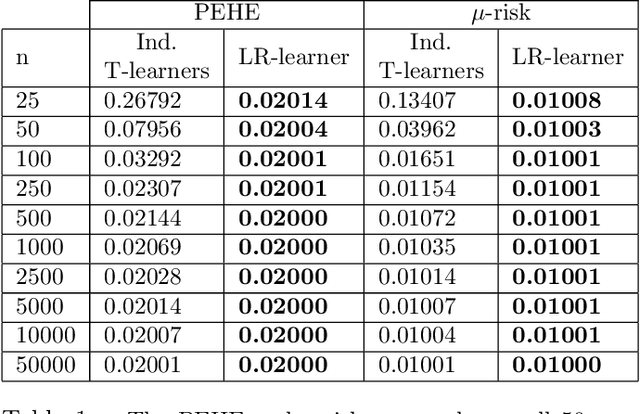
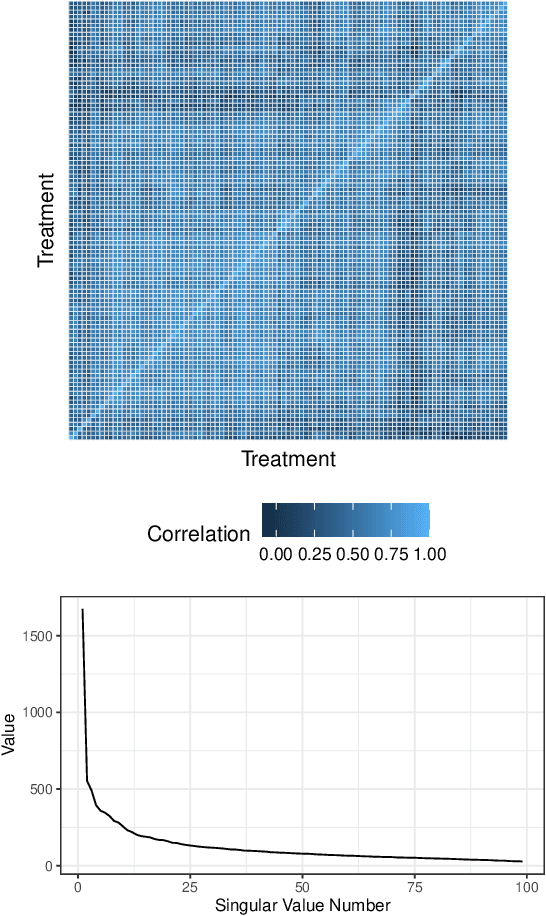
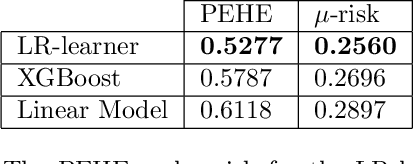
Abstract:Learning heterogeneous treatment effects (HTEs) is an important problem across many fields. Most existing methods consider the setting with a single treatment arm and a single outcome metric. However, in many real world domains, experiments are run consistently - for example, in internet companies, A/B tests are run every day to measure the impacts of potential changes across many different metrics of interest. We show that even if an analyst cares only about the HTEs in one experiment for one metric, precision can be improved greatly by analyzing all of the data together to take advantage of cross-experiment and cross-outcome metric correlations. We formalize this idea in a tensor factorization framework and propose a simple and scalable model which we refer to as the low rank or LR-learner. Experiments in both synthetic and real data suggest that the LR-learner can be much more precise than independent HTE estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge